Niu Ke: Sword finger offer bit operation exercise 👇

one ️⃣ JZ65 Title: 👇

Analysis: we can see that this topic requires to calculate the sum of two numbers, and ordinary topics can calculate the sum of two numbers and link two numbers with "+". However, this topic requires that arithmetic operators can not be used, so we can realize this topic with the help of bit operators and displacement operators
We assume that the two numbers that need to be added are 0 and 1, respectively
| 1+0 | 1^0 | correct |
| 0+1 | 0^1 | correct |
| 0+0 | 0^0 | correct |
| 1+1 | 1^1 | error |

❓ Through four groups of summation operations, it can be found that bitwise XOR (^) can complete the binary without carry after partial addition. When the result of addition has carry, it cannot be completed. How should we solve this problem?
❓ When we look at carry, we always carry to the left. What operator can complete the left shift of binary numbers?
The answer is: the shift left symbol in the displacement operator (< <)
👉 To sum up, we can get two formulas:
Calculate the sum of two numbers: x^y
Carry: (X & Y) < < 1
public class Solution {
public static int Add(int num1,int num2) {
int result = 0;
int carry = 1;
while(carry!=0){
result = num1 ^ num2;
carry = (num1&num2)<<1;
num1 = result;
num2 = carry;
}
return result;
}
}Code parsing:
while(carry!=0){
result = num1 ^ num2;
carry = (num1&num2)<<1;
num1 = result;
num2 = carry;
}Here, the loop is used. The sum of two numbers is calculated by bit exclusive or, and the carry is calculated after the bit exclusive or is shifted one bit to the left. The results calculated in these two steps return to the above and continue the calculation. When the value of carry is equal to 0, the loop can be stopped. At this time, the carry work is completed, and the result of exclusive or is the final result
two ️⃣ JZ15 Title: 👇

There are many ways to solve this problem: 👇
Analysis: the purpose of this problem is to let us calculate the number of 1 in the binary variable, such as 15 in the decimal system, and the corresponding binary is 1111 The other positions are 0, so the number of 1 in the binary of 15 is 4, which is the purpose of this problem. Let's see how to solve this problem 👇
👉 Method 1:
public class TestDemo2 {
public static void main(String[] args) {
int n = 15;
int count = 0;
for (int i = 0; i < 32; i++) {
if(((n>>i)&1)==1){
count++;
}
}
System.out.println(count);
}
}👉 Code parsing:
for (int i = 0; i < 32; i++) {
if(((n>>i)&1)==1){
count++;
}
}Here, using the loop, the integer binary has a total of 32 bits. Move n to the right and 1 respectively. Press and & every time you move to the right and 1 to 1. If the result of press and is 1, it proves that the ith bit of n is also 1, the counter count will increase automatically, and finally print out the value of the counter, that is, the number of 1 in the binary of n

👉 Method 2: simplified version of method 1
👋 Shift right with unsigned
public static void main(String[] args) {
int n = 15;
int count = 0;
while(n!=0){
if((n&1)==1){
count++;
}
n = n >>> 1;
}
System.out.println(count);
}The general idea is the same as that of method 1. It depends on n constantly moving to the right and 1 to press the bit. If the result is 1, the counter will increase automatically. Finally, the result of the counter is the number of n binary. Here, unsigned right shift > > > is adopted. For positive numbers, method 1 is exactly the same as method 2, that is, the circular statements are different
👉 Method 3: the method used in the reference book of sword finger offer
public static void main(String[] args) {
int n = 15;
int count = 0;
while(n!=0){
n = n & (n-1);
count++;
}
System.out.println(count);
}In this method n, every time the bitwise and post binary bits are carried out, there will be one less 1. Finally, when it is equal to 0, it means that there is no 1
Print out the value of the counter, that is, the number of 1 in the binary of n

three ️⃣ JZ16 Title: 👇

Analysis: the requirement of the problem is to find the power of a number without using library function
👉 Method 1: direct method
public static double Power1(double base, int exponent) {
if(base==0 && exponent==0){
return 0;
}
double sum = 1;
if(exponent>0){
for (int i = 0; i < exponent; i++) {
sum *= base;
}
}
else if(exponent<0){
for (int i = 0; i > exponent; i--) {
sum /= base;
}
}
else if(exponent==0){
return 1;
}
return sum;
}This method is more conventional, and the values can be obtained successively in three cases of power.
👉 Method 2: recursion
public static double Power2(double base, int exponent){
if(exponent==0){
return 1;
}
if(exponent>0){
return base*Power2(base,exponent-1);
}
if (exponent < 0) return Power2(1 / base, -exponent);
return -1;
}There are still three cases here. When the power number is equal to 0, it is easy to understand. When the power number is greater than 0, take the size of the power number as the termination condition of recursion to see when the power number is equal to 0. The previous power number is reduced and multiplied by base. Finally, the result can be obtained. When the power number is negative, it is the power of the reciprocal of base, so here, use 1/base to find the reciprocal, and then find the power of the corresponding reciprocal
👉 Method 3: bit operation
public static double Power(double base, int exponent) {
double res = 1.0;
for (int i = exponent; i != 0; i /= 2) {
if ((i&1) == 1) {
res *= base;
}
base *= base;
}
if (exponent < 0) {
res = 1 / res;
}
return res;
}Take the power number as the condition of the cycle, enter the cycle, and judge that if you get the 1 counter res in the power number binary, it will accumulate into the base. After this judgment, the base performs the square operation, and finally judge at the end of the cycle. If the power number is less than 0, the result is to obtain the reciprocal of the positive power number
Two cases of positive and negative power numbers are illustrated:
Positive number:

Negative number:

4️⃣ JZ 56: 👇


Demand analysis: this problem requires us to print out two numbers that only appear once in the array
❓ Let's simplify the problem first: think about how to find out if there is only one number in the array?
❗ ️ Because the subject has requirements for time complexity, simple array traversal + counter can not be applied to this subject
👉 So here we use the bitwise operator: bitwise XOR (^)
Bitwise XOR is to find the difference between two binary numbers. The same is 0 and the difference is 1. If two identical numbers (that is, the binary sequence is exactly the same) are bitwise XOR, the binary sequence of the result is 0 and the corresponding result is 0. Let's think about another problem. If 0 is exclusive or any non-0 digit, the binary sequence obtained is the significant digit of the non-0 digit binary sequence, that is, the non-0 digit itself 👇
The result of bitwise XOR of two identical numbers is: 0
0 bitwise exclusive or any non-0 number. The result is: the non-0 number itself
👉 Based on these two conclusions, we can draw a conclusion that if we need to print the numbers that appear once in the array, that is, use the first element of the array to cycle back and press the elements of each array after the XOR, so that the final result of the XOR is the number that appears only once
The code is as follows: (an element that appears only once in the array)
public class TestDemo {
public static void main(String[] args) {
int[] arr = {1,2,2,3,8,3,8};
int sum = arr[0];
for (int i = 1; i < arr.length; i++) {
sum = sum ^ arr[i];
}
System.out.println(sum);
}
}The results are: 1
👉 The result is the number that appears only once in the array: 1

❓ We know a number that only appears once. What about the two that appear once?
👉 Answer: it is roughly the same as the above method. First, XOR each element of the array to get a value. In fact, this value is the result of the mutual XOR of the two numbers that only appear once. Therefore, we think like this. From the binary sequence of the obtained value, find the binary 1 that appears for the first time from right to left, Because the binary bits of two numbers are different during XOR, the result is 1, so the array is divided into two groups with the help of this different 1. In this way, it can ensure that the two numbers that appear once are divided into two groups. The two groups are XOR, and the two results of the last XOR are the two numbers that appear once
The code is as follows:
import java.util.Arrays;
public class TestDemo {
public static void main(String[] args) {
int[] arr = {1,2,2,3,8,3,8,9};
int[] ret = new int[2];
int sum = arr[0];
for (int i = 1; i < arr.length; i++) {
sum = sum ^ arr[i];
}
//Get the first 1 in the binary
sum -= (sum) & (sum-1);
//Group arrays
for (int i = 0; i < arr.length; i++) {
//Group the array elements that are not 1 in the same position as the binary
if ((sum&arr[i])==0){
ret[0] ^= arr[i];
}
//The array elements in the same position as the binary are divided into a group of 1
else{
ret[1] ^= arr[i];
}
}
Arrays.sort(ret);
System.out.println(Arrays.toString(ret));
}
}The results are: 1,9

5️⃣ JZ 64 👇

Requirements analysis: let's not use any multiplication and division operators, keywords and judgment statements
❓ Thinking: how to solve the problem?
👉 Answer: use bitwise operators to solve: > >
We can see that what needs to be summed is an arithmetic sequence, that is, it is solved by the summation formula of the arithmetic sequence we are familiar with: 👇
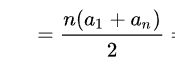
❗ However, multiplication and division are not allowed in the topic, so we can simplify the formula, that is, it can be equal to: n*(n+1)/2 = (n^2+n)/2
❓ reflection: (/ 2) what can be used instead
👉 Answer: the result > > 1 is divided by 2, because moving 1 bit to the right, the corresponding binary bit moves 1 bit to the right, that is, it is twice less
The code is as follows:
public class Solution {
public int Sum_Solution(int n) {
return ((int)(Math.pow(n,2))+n)>>1;
}
}Because the result of using the square formula is a floating-point type, one-step forced type conversion is required here
These five questions are related to the bit operation in the sword finger offer. The blogger has just started to brush the questions. If there is any problem with the code, please contact the blogger at any time. If you are helpful, please click three times. Thank you for your support!!!!
💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕💕