Self-Improvement

Money is not life's report card.
Money cannot be used to measure whether life is wonderful or not.

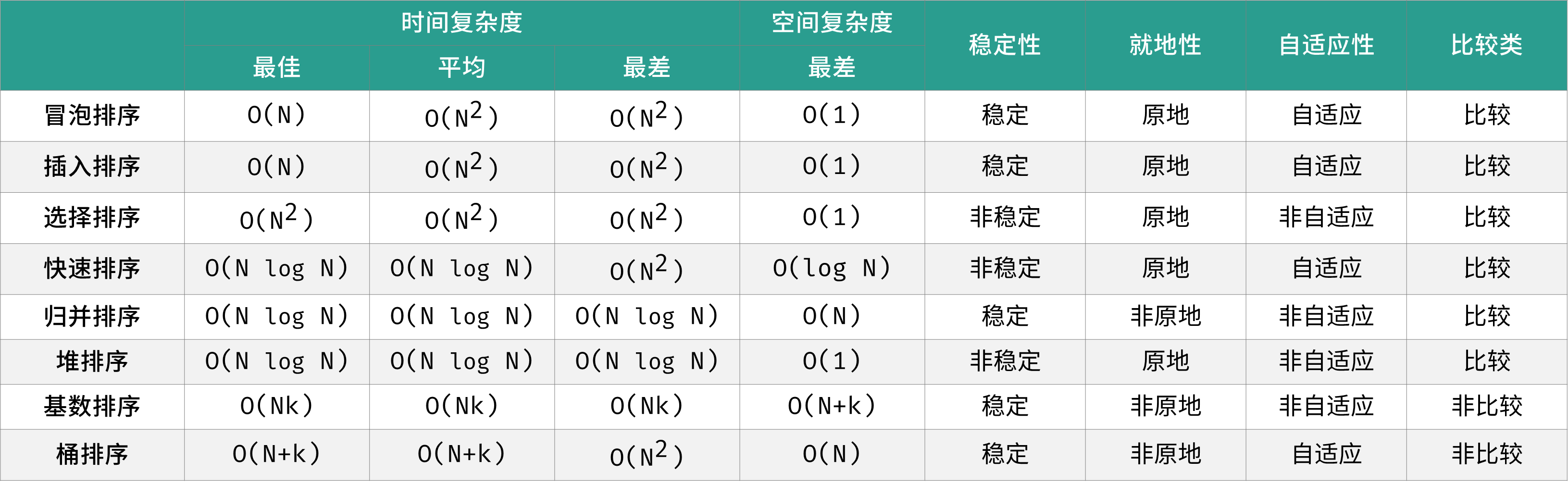
Common algorithms

The following figure shows the sorting process of common sorting algorithms under the four types of input data of "random disorder", "near order", "complete reverse order" and "few unique".

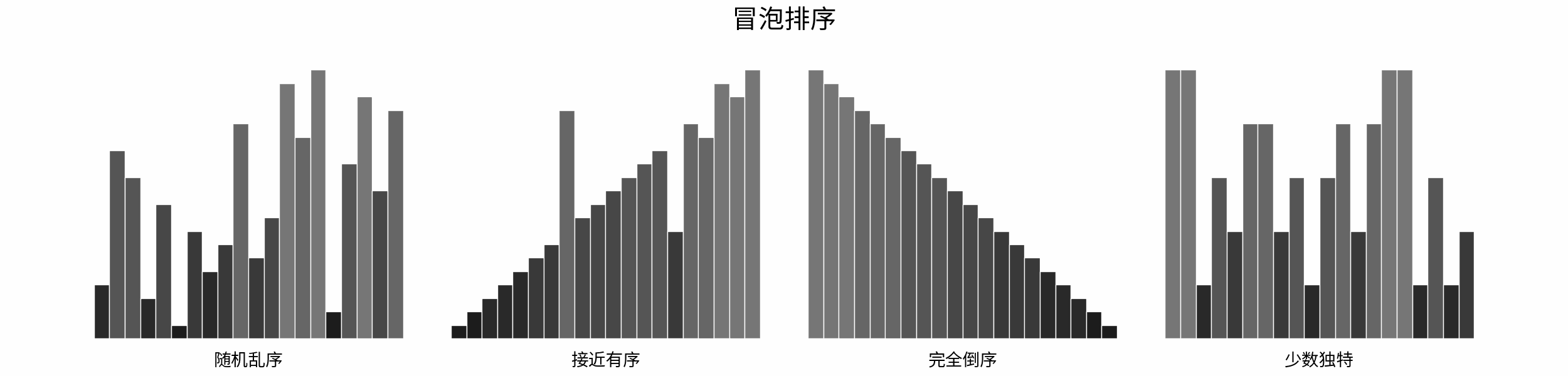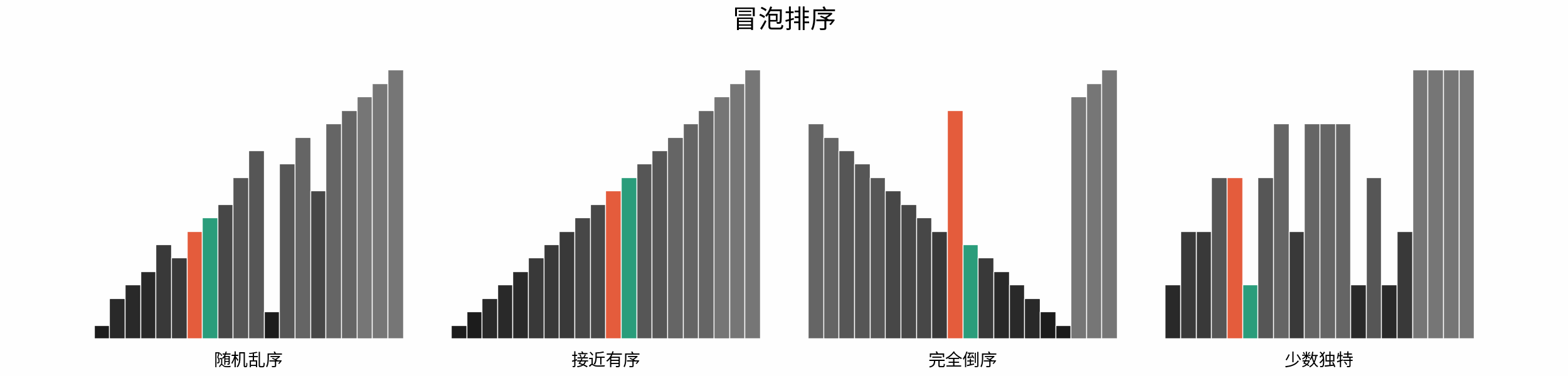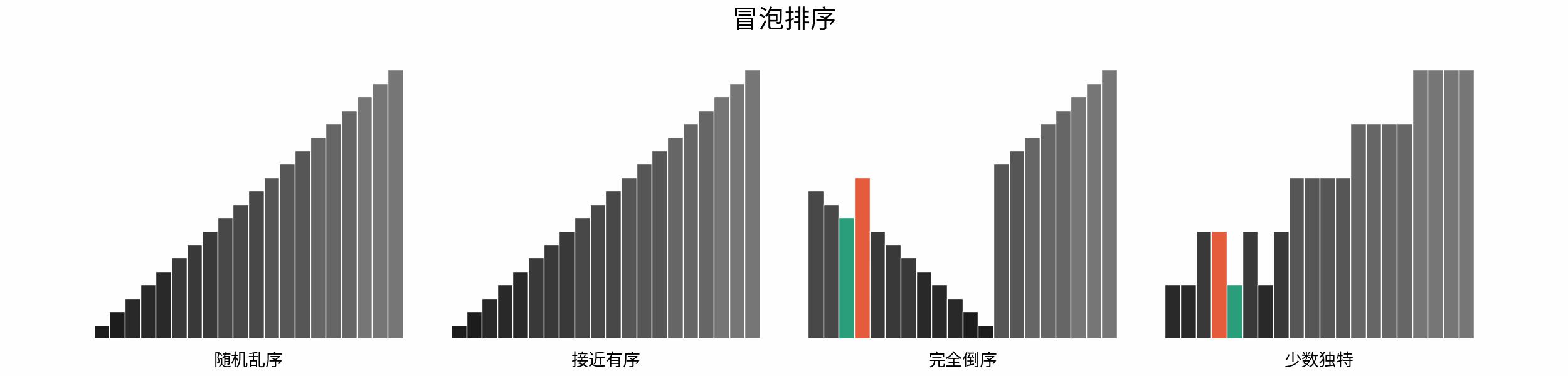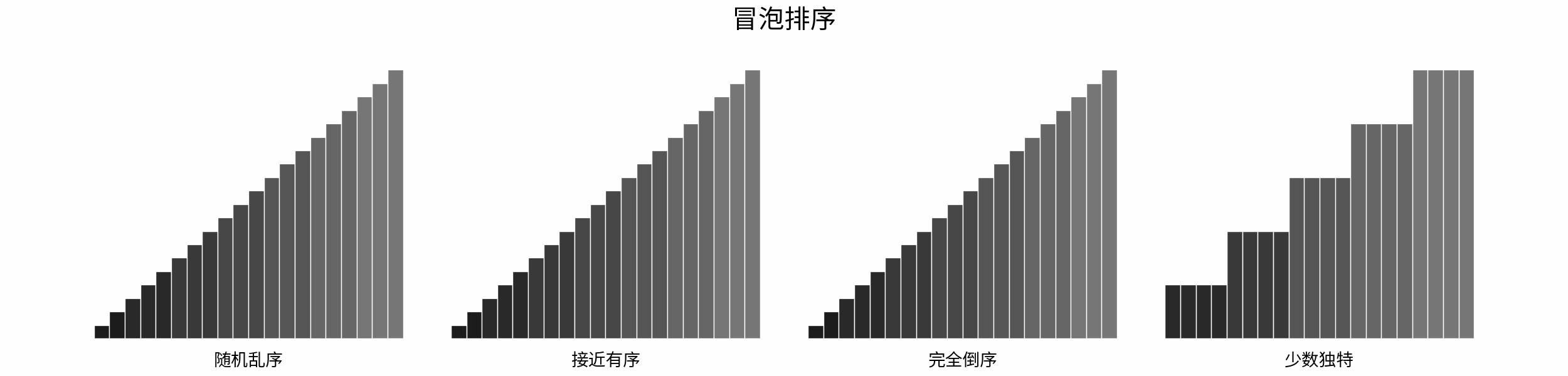
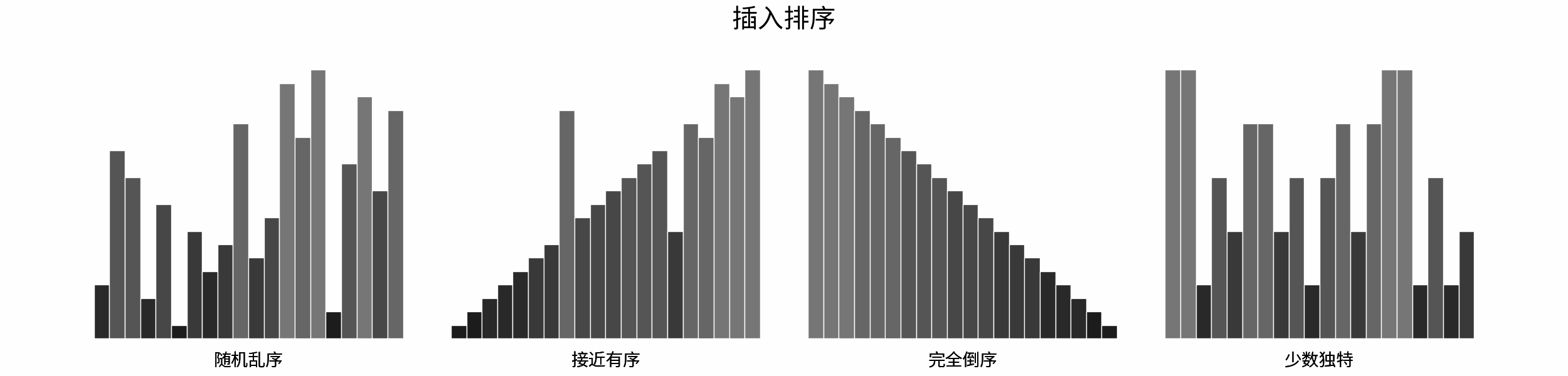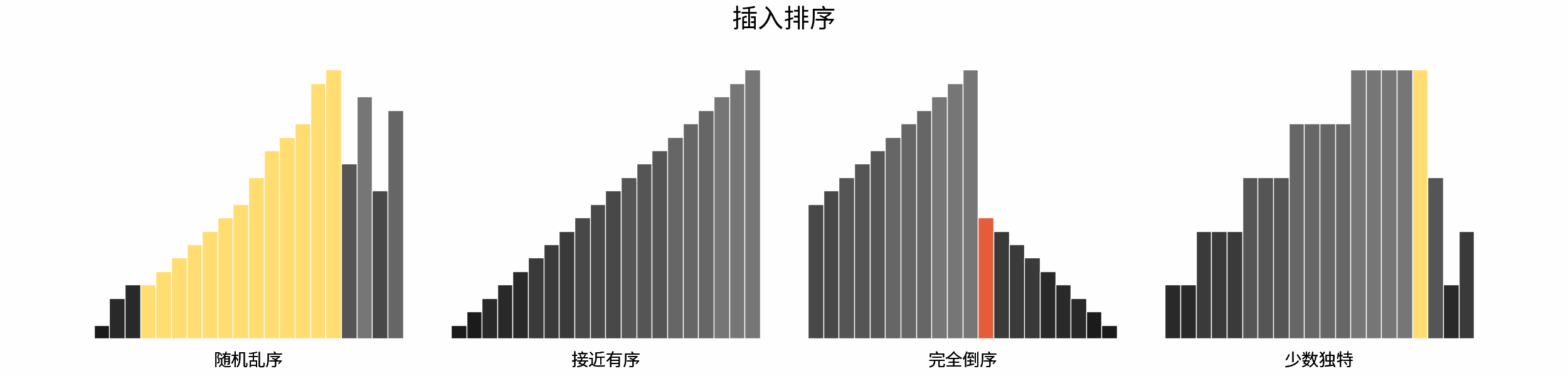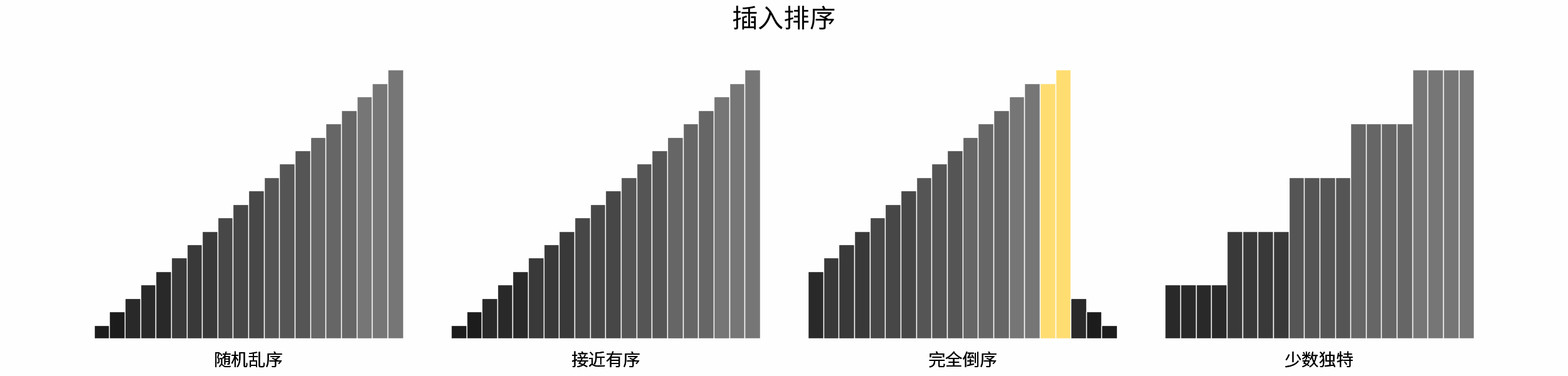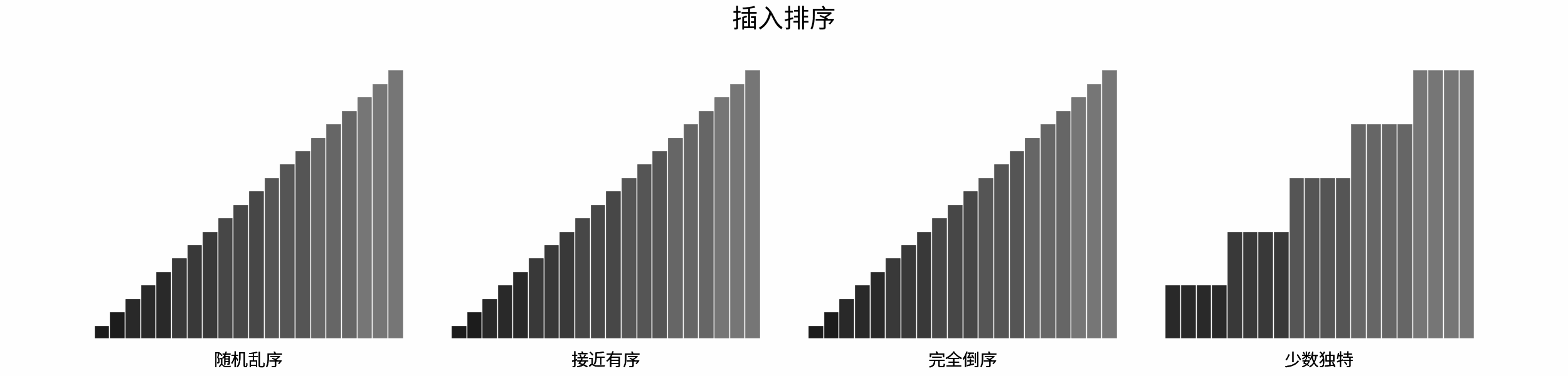
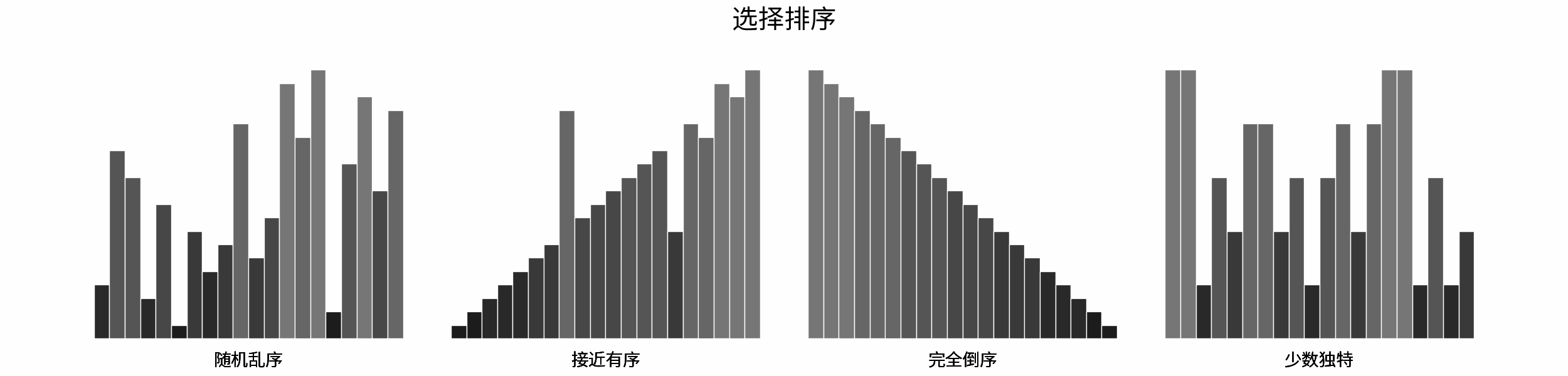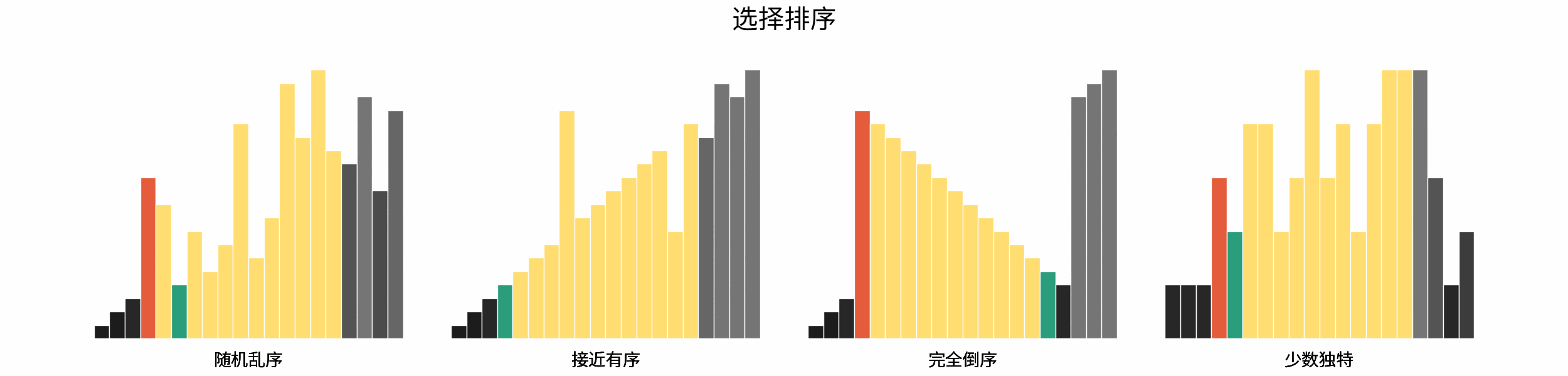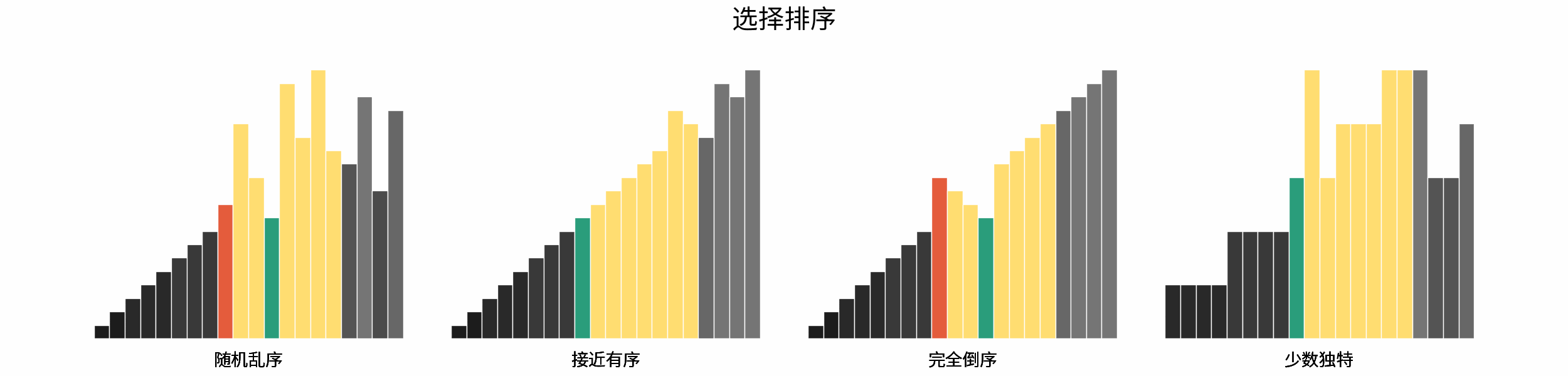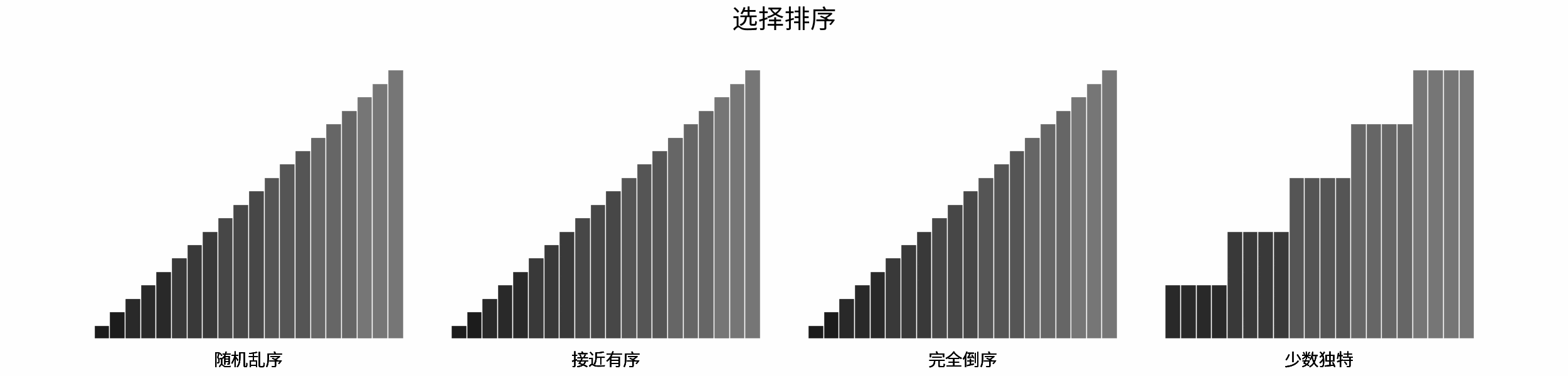
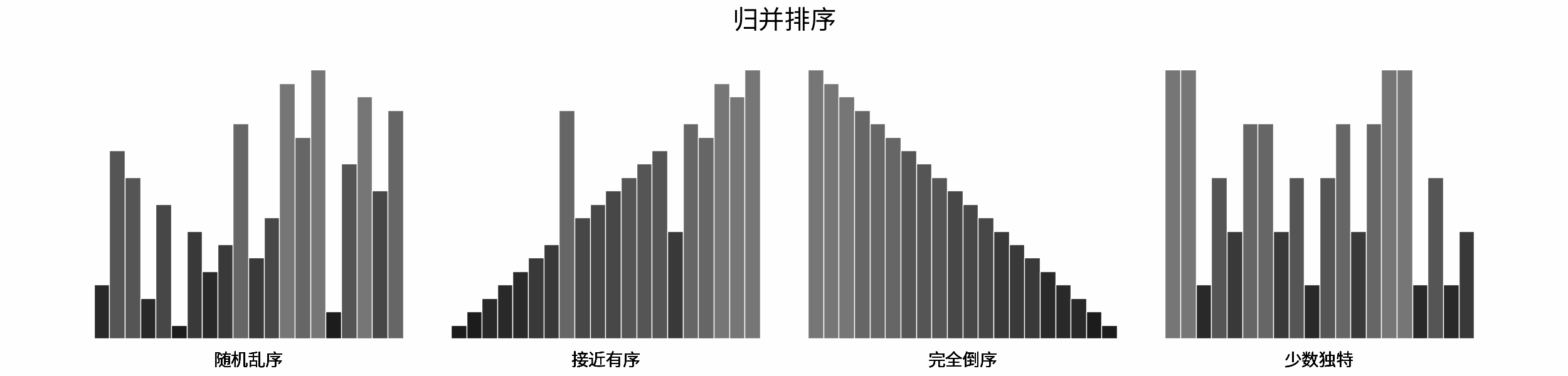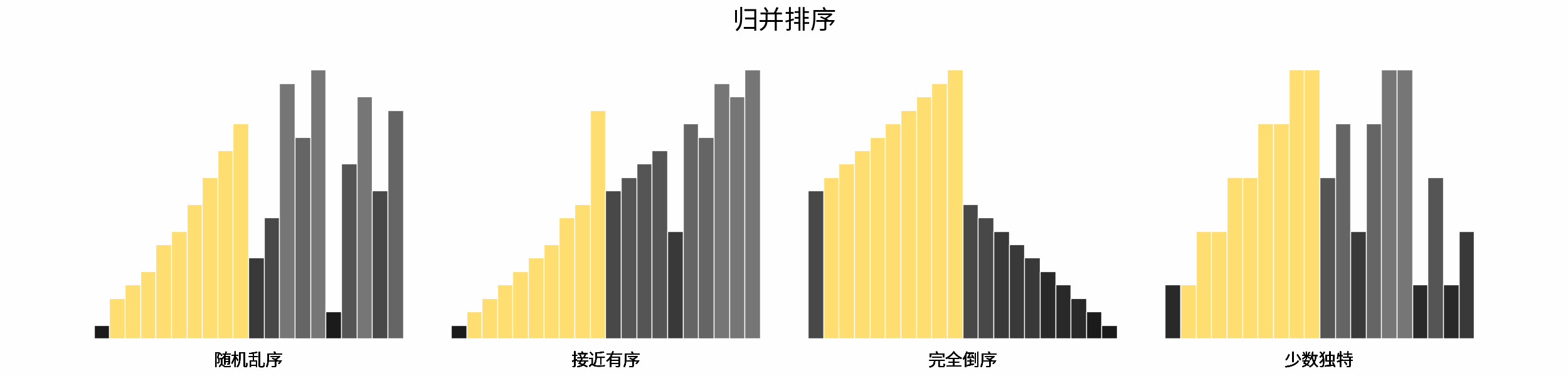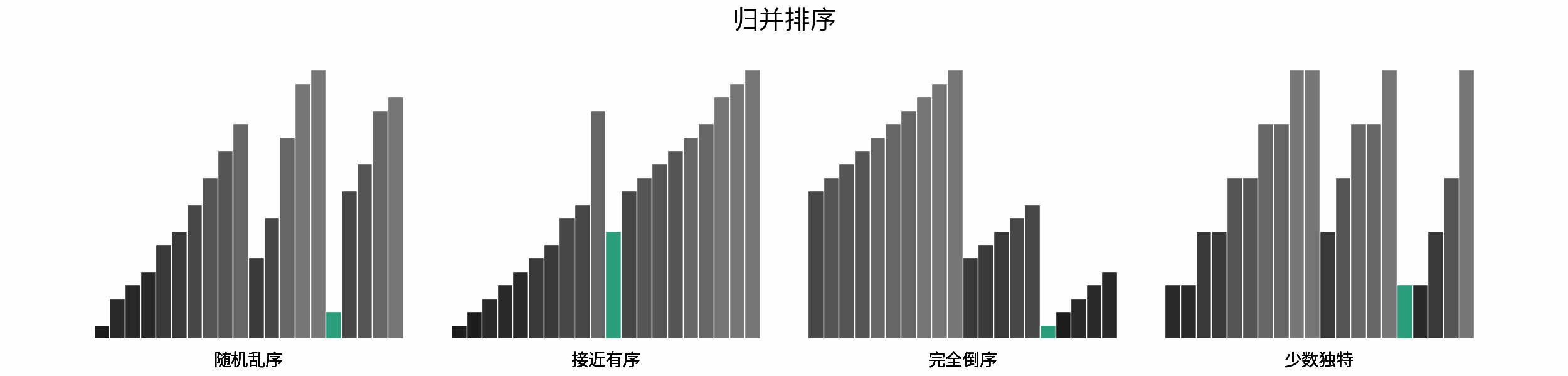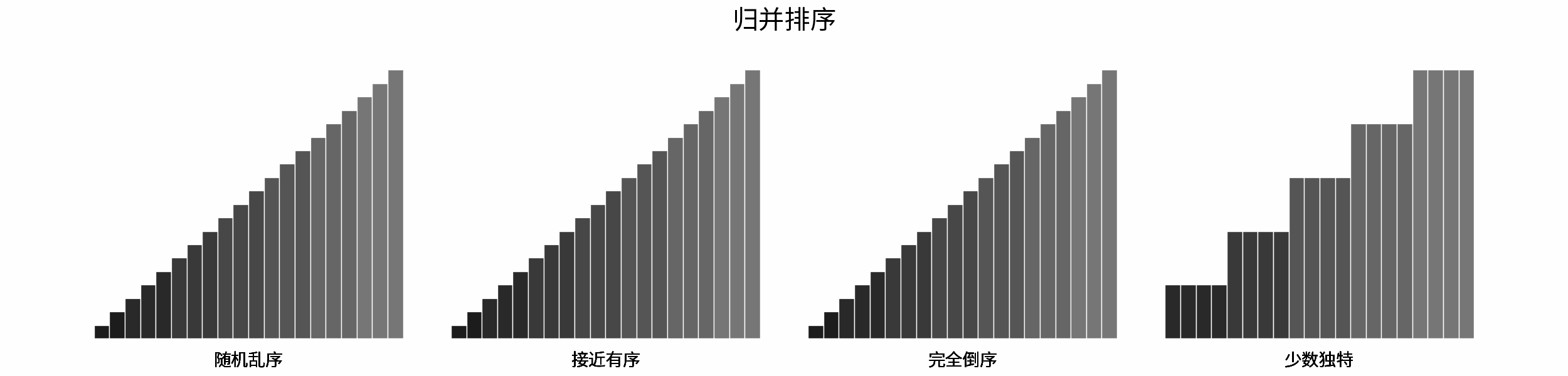
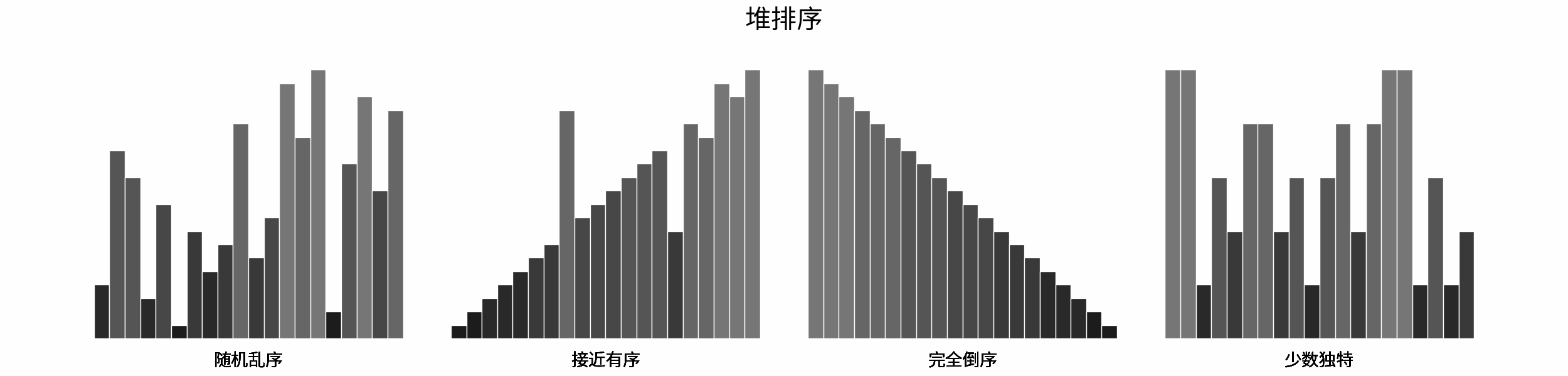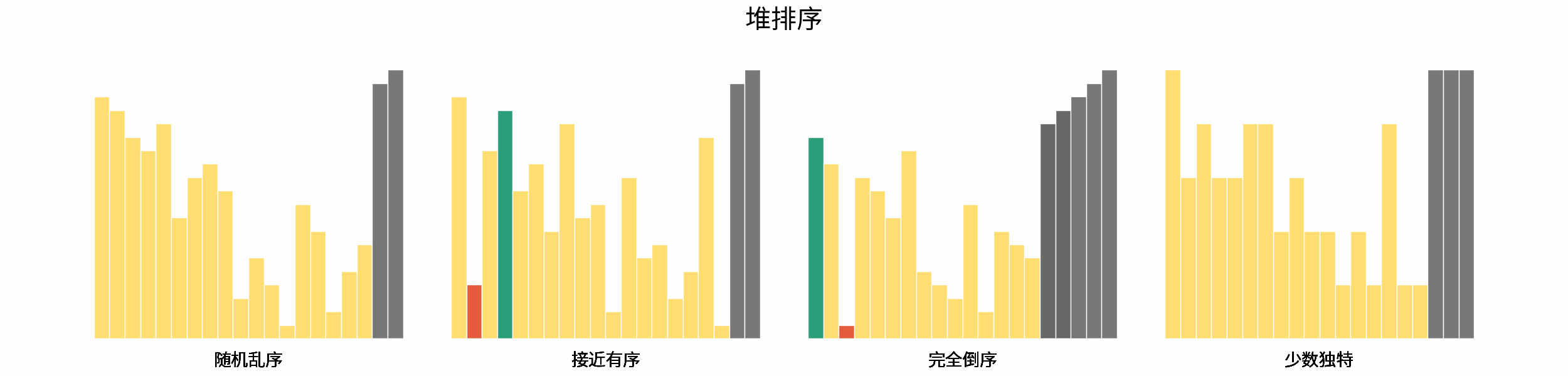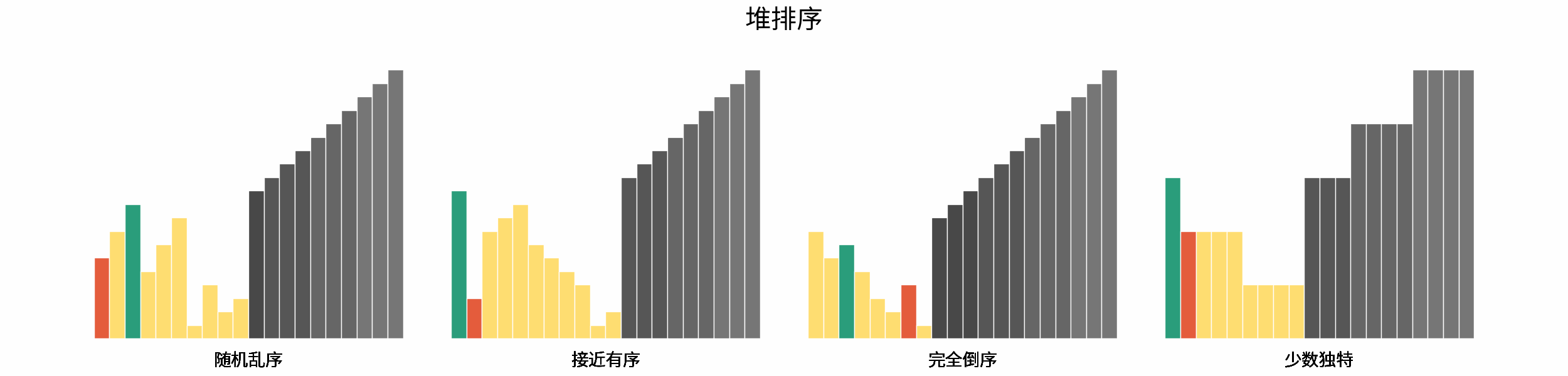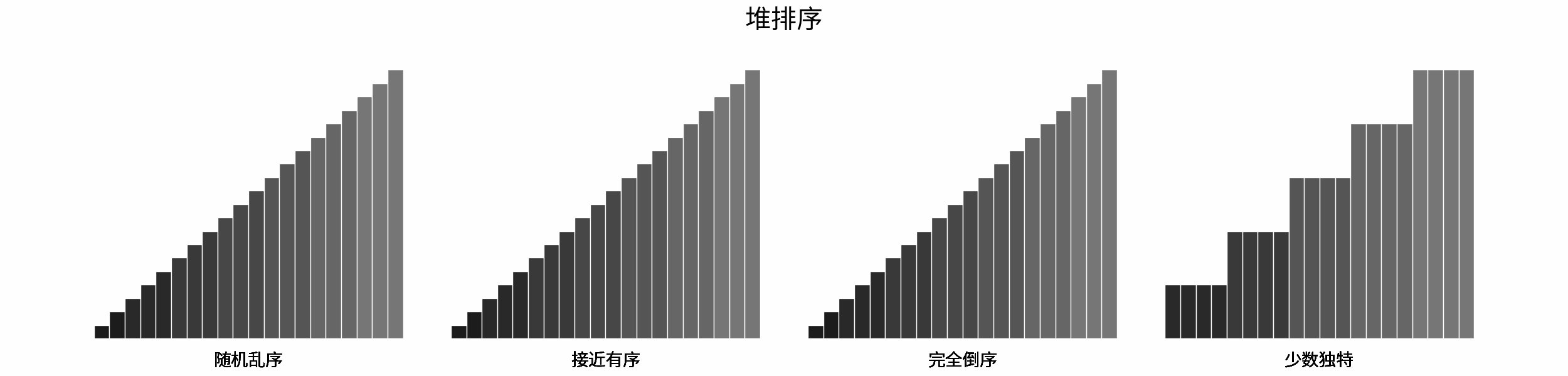
Sorting algorithms can be classified mainly according to stability, locality and adaptability.

• It has stability, that is, the relative position of equal elements does not change;
• Local, i.e. no additional auxiliary space is used;
• It is adaptive, that is, the time complexity is affected by the element distribution;

Bubble sort:

AC template:

void bubbleSort(int[] nums) {
	int N = nums.length;
	for (int i = 0; i < N - 1; i++) {  
		for (int j = 0; j < N - i - 1; j++) { 
			if (nums[j] > nums[j + 1]) {
				int tmp = nums[j];
				nums[j] = nums[j + 1];
				nums[j + 1] = tmp;
			}
		}
	}
}

• Time complexity: O(N^2)
• Space complexity: O(1)

Bubble sorting of optimized version:

void bubbleSort(int[] nums) {
	int N = nums.length;
	for (int i = 0; i < N - 1; i++) {
		boolean flag = false; // Initialization flag bit
		for (int j = 0; j < N - i - 1; j++) {
			if (nums[j] > nums[j + 1]) {
				int tmp = nums[j];
				nums[j] = nums[j + 1];
				nums[j + 1] = tmp;
				flag = true;  // Record exchange element
			}
		}
		if (!flag) break;     // If the inner loop does not exchange any elements, it jumps out
	}
}

If no swap operation is performed in an inner loop, the array has been sorted

Quick sort:

Algorithm idea: sentinel partition and recursion

Sentinel division:
Take an element of the array (generally the first element) as the reference number, move all elements less than the reference number to its left, and elements greater than the reference number to its right.

Recursion:
Sentinel partitioning is performed recursively on the left subarray and the right subarray, respectively

AC template:

void quickSort(int[] nums, int l, int r) {
    // Terminate recursion when subarray length is 1
    if (l >= r) return;
    // Sentinel division operation
    int i = partition(nums, l, r);
    // Recursive left (right) subarray performs sentinel partitioning
    quickSort(nums, l, i - 1);
    quickSort(nums, i + 1, r);
}

int partition(int[] nums, int l, int r) {
    // Take nums[l] as the reference number
    int i = l, j = r;
    while (i < j) {
    // Because we use the leftmost number as the benchmark
    // So first j --, then i + + (move J first, then i)
        while (i < j && nums[j] >= nums[l]) j--;
        while (i < j && nums[i] <= nums[l]) i++;
        swap(nums, i, j);
    }
    swap(nums, i, l);
    return i;
}

void swap(int[] nums, int i, int j) {
    // Swap nums[i] and nums[j]
    int tmp = nums[i];
    nums[i] = nums[j];
    nums[j] = tmp;
}

Common optimization methods for quick sorting include "Tail Call" and "random benchmark".

Tail Call:
Control the recursion depth, and each recursion is short array

void quickSort(int[] nums, int l, int r) {
    // Terminate recursion when subarray length is 1
    while (l < r) {
        // Sentinel division operation
        int i = partition(nums, l, r);
        // Recurse only to shorter subarrays, controlling the recursion depth
        if (i - l < r - i) {
            quickSort(nums, l, i - 1);
            l = i + 1;
        } else {
            quickSort(nums, i + 1, r);
            r = i - 1;
        }
    }
}

Random reference number:
Find a random reference number in the subarray for each round

int partition(int[] nums, int l, int r) {
    // Randomly select any index in the closed interval [l, r] and exchange it with num [l]
    int ra = (int)(l + Math.random() * (r - l + 1));
    swap(nums, l, ra);
    // Take nums[l] as the reference number
    int i = l, j = r;
    while (i < j) {
        while (i < j && nums[j] >= nums[l]) j--;
        while (i < j && nums[i] <= nums[l]) i++;
        swap(nums, i, j);
    }
    swap(nums, i, l);
    return i;
}

Merge sort:

Algorithmic thought: divide and conquer

Divide: continuously divide the array from the midpoint

Rule: merge the left and right shorter sort arrays into a longer sort array

AC template:

void mergeSort(int[] nums, int l, int r) {
    // Termination conditions
    if (l >= r) return;
    // recursive partitioning 
    int m = (l + r) / 2;
    mergeSort(nums, l, m);
    mergeSort(nums, m + 1, r);
    // Merge subarrays
    int[] tmp = new int[r - l + 1]; // Temporary storage of interval elements to be merged
    for (int k = l; k <= r; k++)
        tmp[k - l] = nums[k];
    int i = 0, j = m - l + 1;       // The two pointers point to the first element of the left / right sub array respectively
    for (int k = l; k <= r; k++) {  // Traverse and merge left / right subarrays
        if (i == m - l + 1)
            nums[k] = tmp[j++];
        else if (j == r - l + 1 || tmp[i] <= tmp[j])
            nums[k] = tmp[i++];
        else {
            nums[k] = tmp[j++];
        }
    }
}

1, Sword finger Offer 40. Minimum number of k

Question:

Enter the integer array arr to find the minimum number of k. For example, if you enter 8 numbers: 4, 5, 1, 6, 2, 7, 3 and 8, the minimum 4 numbers are 1, 2, 3 and 4.

Example 1:

Input: arr = [3,2,1], k = 2
 Output:[1,2] perhaps [2,1]

Example 2:

Input: arr = [0,1,2,1], k = 1
 Output:[0]

Limitations:

0 <= k <= arr.length <= 10000
0 <= arr[i] <= 10000

Solution:

Problem solving idea: quick sorting
AC Code:

class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        int len = arr.length;
        if(k >= len) return arr;
        return quick_sort(arr, k, 0, len - 1);
    }
    int[] quick_sort(int[] nums, int k, int left, int right){
        int i = left, j = right;
        while(i < j){
            while(i < j && nums[j] >= nums[left]) j--;
            while(i < j && nums[i] <= nums[left]) i++;          
            if(i < j) swap(nums, i, j);
        }
        swap(nums, left, i);
        if(k < i) return quick_sort(nums, k, left, i-1);
        else if(k > i) return quick_sort(nums, k, i+1, right);
        return Arrays.copyOf(nums, k);
    }
    void swap(int[] nums, int i, int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

2, Sword finger Offer 41. Median in data stream

Question:

How to get the median in a data stream? If an odd number of values are read out from the data stream, the median is the value in the middle after all values are sorted. If an even number of values are read from the data stream, the median is the average of the middle two numbers after all values are sorted.

For example,

The median of [2,3,4] is 3

The median of [2,3] is (2 + 3) / 2 = 2.5

Design a data structure that supports the following two operations:

• void addNum(int num) - adds an integer from the data stream to the data structure.
• double findMedian() - returns the median of all current elements.

Example 1:

input
["MedianFinder","addNum","addNum","findMedian","addNum","findMedian"]
[[],[1],[2],[],[3],[]]
Output:[null,null,null,1.50000,null,2.00000]

Example 2:

Input:
["MedianFinder","addNum","findMedian","addNum","findMedian"]
[[],[2],[],[3],[]]
Output:[null,null,2.00000,null,2.50000]

Limitations:

At most addNum,findMedian 50000 calls.

Solution:

Problem solving idea: large top pile + small top pile
AC Code:

class MedianFinder {

    Queue<Integer> A, B;
    /** initialize your data structure here. */
    public MedianFinder() {
        A = new PriorityQueue<>(); // Large top reactor
        B = new PriorityQueue<>((x, y) -> (y - x)); // Small top pile
    }
    
    public void addNum(int num) {
        if(A.size() != B.size()){ // A less B more
            A.add(num);
            B.add(A.poll());
        }else{
            B.add(num);
            A.add(B.poll());
        }
    }
    
    public double findMedian() {
        return A.size() != B.size() ? A.peek() : (A.peek() + B.peek())/2.0;
    }
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */

3, Sword finger Offer 45. Arrange the array into the smallest number

Question:

Input a non negative integer array, splice all the numbers in the array into a number, and print the smallest of all the numbers that can be spliced.

Example 1:

input: [10,2]
output: "102"

Example 2:

input: [3,30,34,5,9]
output: "3033459"

Tips:

0 < nums.length <= 100

explain:

• The output can be very large, so you need to return a string instead of an integer
• The spliced numbers may have leading zeros, and the leading zeros do not need to be removed in the final result

Solution:

Problem solving idea: quick sorting
AC Code:

class Solution {
    public String minNumber(int[] nums) {
        int len = nums.length;
        String[] strs = new String[len]; // Array to string array
        for(int i = 0; i < len; i++) strs[i] = String.valueOf(nums[i]); 
        quickSort(strs, 0, len-1);
        StringBuilder res = new StringBuilder(); // String array to string
        for(String str : strs) res.append(str);
        return res.toString();
    }
    void quickSort(String[] strs, int l, int r){
        if(l >= r) return; 
        int i = l, j = r;
        while(i < j){
            while(i < j && (strs[l] + strs[j]).compareTo(strs[j] + strs[l]) <= 0) j--; // l+j < j+l
            while(i < j && (strs[i] + strs[l]).compareTo(strs[l] + strs[i]) <= 0) i++; // i+l < l+i
            if(i < j) swap(strs, i, j);
        }
        swap(strs, i, l);
        quickSort(strs, l, i-1);
        quickSort(strs, i+1, r);
    }
    void swap(String[] strs, int i, int j){
        String temp = strs[i];
        strs[i] = strs[j];
        strs[j] = temp;
    }
}

Another solution: built-in function

class Solution {
    public String minNumber(int[] nums) {
        String[] strs = new String[nums.length];
        for(int i = 0; i < nums.length; i++)
            strs[i] = String.valueOf(nums[i]);
        Arrays.sort(strs, (x, y) -> (x + y).compareTo(y + x));
        StringBuilder res = new StringBuilder();
        for(String s : strs)
            res.append(s);
        return res.toString();
    }
}

4, Sword finger Offer 61. Shunzi in playing cards

Question:

Draw 5 cards randomly from several pairs of playing cards to judge whether it is a surplus, that is, whether the 5 cards are continuous. 2 ~ 10 is the number itself, a is 1, J is 11, Q is 12, K is 13, and DA and Xiao Wang are 0, which can be regarded as any number. A cannot be regarded as 14.

Example 1:

input: [1,2,3,4,5]
output: True

Example 2:

input: [0,0,1,2,5]
output: True

Limitations:

The array length is 5 

The number of arrays is [0, 13] .

Solution:

Problem solving idea: Set + traversal
AC Code:

class Solution {
    public boolean isStraight(int[] nums) {
        Set<Integer> repeat = new HashSet<>();
        int max = 0, min = 14;
        for(int num : nums){
            if(num == 0) continue; // Skip big and small Wang
            max = Math.max(num, max);
            min = Math.min(num, min);
            if(repeat.contains(num)) return false; // Shunzi can't have the same card
            repeat.add(num);
        }
        return max -min < 5;
    }
}

• Time complexity O(1): the number of given cards in this question N ≡ 5; Traversing the array uses O(N) = O(5) = O(1) time.
• Space complexity O(1): the auxiliary Set used for duplicate judgment uses O(N) = O(1) additional space.

Problem solving ideas: sorting + traversal
AC Code:

class Solution {
    public boolean isStraight(int[] nums) {
        int joker = 0; // The number of big and small kings, shunzi starting subscript
        Arrays.sort(nums);
        for(int i = 0; i < 4; i++){
            if(nums[i] == 0){ // Meet big and small king
               joker++; 
               continue; 
            }
            if(nums[i] == nums[i+1]) return false; // There are duplicate elements
        }
        return nums[4] - nums[joker] < 5;
    }
}