System master data structure 3 linear table C + + implementation

(this article and each subsequent article have such a structure. First, we will talk about the logical structure, then preliminarily understand the physical structure, then realize the code, and finally re understand the advantages and disadvantages of the physical structure in combination with the code. The code of this chapter and the exercise code are packaged into a file: Linear table and exercise code)

1. Logical structure

Linear table: a finite sequence of zero or more data elements of the same data type.

(there is order between elements. The first element has no predecessor, the last element has no successor, and other elements have only one predecessor and one successor.)

Empty table: the number of linear table elements n is defined as the length of the linear table. When n=0, it is called an empty table
In a more complex linear table, data elements can be composed of multiple data items.

(linear table is a kind of logical structure. Its physical structure can be realized by sequential table or linked list. Do not confuse linear table and sequential table)

2. Storage structure

(see the storage structure in combination with the code implementation in Section 3)

2.1 sequential storage

The sequential storage structure of linear table refers to the storage of data elements of linear table at one time with a section of storage unit with continuous addresses.

(the logical order and physical order are the same when the linear table is stored sequentially)

The sequential table storage structure is a random access storage structure, because the bytes occupied by each element are the same, so it is easy to operate the elements at any position.
Basic structure: similar to array.

2.2 chain storage

Chained storage: a group of arbitrary storage units are used to store the data elements of the linear table. For the data element ai, in addition to storing the data element information, it also stores the subsequent position (i.e. pointer).
Basic structure: the linked list is composed of n nodes. Each node has a data field to store the value of the element and a pointer field to store the subsequent address of the element, that is, the pointer. The pointer to the first node is called the head pointer, and the pointer to the last node points to NULL. (primary single linked list structure)

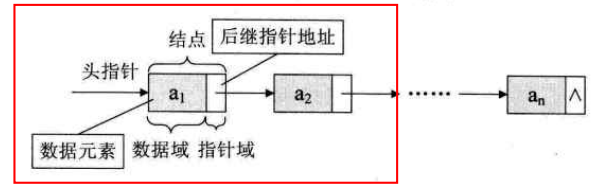
Head node structure: we add a head node before the first node in the list. The data field of the head node stores the number of elements in the linked list or does not store any information. The pointer field stores the position of the first node. At this time, the head pointer points to the head node. Such a structure is more standardized. As for why we realize in the code, the linked list usually has a head node in future learning.

3. Implementation of linear table

3.1 implementation of sequential storage structure

3.1.1 static distribution

#define MaxSize 50
typedef int ElemType;	
//ElemType can be any data type. For example, it is set to int here
typedef struct {
	ElemType data[MaxSize];//An array of storage elements
	int length;//Number of record elements
}SqList;

Static allocation is convenient for everyone to understand the implementation of the sequential storage structure of the linear table, but when the number of elements exceeds MaxSize, data overflow will occur.

3.1.2 dynamic allocation

#define InitSize 50
#define IncreaseSize 10 / / the capacity added at one time when the capacity is insufficient
typedef int ElemType;

typedef struct {
	ElemType *data;
	int MaxSize, length;//Length records the number of elements, and maxsize is the current linear table capacity. length<=MaxSize
}SqList;

Dynamic allocation will expand when the capacity is insufficient, so the next linear table operations are based on the sequential storage structure of dynamic allocation.

3.2 implementation of sequential storage operation

(Preface: about SqList & L, it means reference. The type of L is SqList. If the value of L in the function is changed, the value of L in the main function will also change)

(SqList L, parameter passed. The type of L is SqList. The change of L value will not affect L in the main function, but if the value of L - > data changes, the value of the original function L - > data will also change.)

(SqList *L, where l is an address. Changing the value of l will not affect the value of the main function, but if the value of L - > data changes, the value of the original function L - > data will also change. In fact, the change of parameters will not affect the main function, but the change of the value stored in some addresses will affect the main function. We can understand it through our own experiments to facilitate our operation.)

#define InitSize 50
#define IncreaseSize 10 
#define OK 1 			// In order to facilitate function writing, it indicates that the operation is successful
typedef int Status;		//Status is the return value type of the function and can be any type. int is used here
typedef int ElemType;

typedef struct {
	ElemType *data;
	int MaxSize, length;
}SqList;

3.2.1 initialize linearity table

/*
Get a linear table
*/
Status InitSqList(SqList& L) {
	L.data = (ElemType*)malloc(sizeof(ElemType)*InitSize); //Allocate initial memory
	if (!L.data)					 //If the allocation fails, the program ends
		return ERROR;
	L.MaxSize = InitSize;			//Capacity assignment
	L.length = 0;					//Element assignment 
	return OK;
}
int main() {
	SqList L ;
	int x = InitSqList(L);
	cout << x << endl;				//The print result is 1
}

3.2.2 insert elements

Status ListInsert(SqList& L, int i, ElemType e) {
	if (i < 1 || i > L.length + 1)
		return ERROR;				//The position of the inserted element should be legal. When i=1, it should be inserted at the front, and when i=length+1, it should be inserted at the end
	if (L.length >= L.MaxSize) {	//Insufficient capacity
		//Reallocate memory
		L.data = (ElemType*)realloc(L.data, sizeof(ElemType) * (L.MaxSize + IncreaseSize));
		if (!L.data) return ERROR;
		L.MaxSize = L.MaxSize + IncreaseSize;
	}
	for (int j = L.length; j >= i; j++) {//The elements at position i and after move the position of an element backward
		L.data[j] = L.data[j - 1];
	}
	L.data[i - 1] = e;				//The index of the ith position is i-1
	L.length++;
	return OK;
}

To verify that what we wrote is correct, we write a function that prints a linear table

Status ListPrint(SqList L) {
	for (int i = 0; i < L.length; i++) {
		cout << L.data[i] << "";
		cout << "\t" << "";
	}
	cout << "" << endl;
	return OK;
}

And then call the function.

int main() {
	SqList L ;
	int x = InitSqList(L);
	for (int i = 0; i < 55; i++) {
		ListInsert(L, i + 1, i + 1);
	}
	ListPrint(L);//Print out 1 2 3 55 indicates that the function is written correctly
}

3.2.2 delete

/*
Delete i location element
*/
Status ListDelete(SqList& L, int i) {

	if (i < 1 || i > L.length) //Illegal location
		return ERROR;
	
	for (int j = i; j < L.length; j++) {//Both the i+1 position and the following move the position of an element forward
		L.data[j - 1] = L.data[j];
	}
	L.length--;
	return OK;
}

Verify it at the same time

int main() {
	SqList L ;
	int x = InitSqList(L);
	for (int i = 0; i < 55; i++) {
		ListInsert(L, i + 1, i + 1);
	}
	ListPrint(L);
	ListDelete(L,30);//Delete the element at position 30
	ListPrint(L);//Print results 1 2 29 31 ...  fifty-five
}

3.3.2 search by value

int GetElem(SqList L, ElemType e) {
	for (int i = 0; i < L.length; i++) {
		if (L.data[i] == e) {
			return i;
		}
	}
	return -1;//Indicates that it was not found
}

Check it

int main() {
	SqList L ;
	int x = InitSqList(L);
	for (int i = 0; i < 55; i++) {
		ListInsert(L, i + 1, i + 1);
	}
	ListPrint(L);
	ListDelete(L,30);
	ListPrint(L);
	cout << GetElem(L, 30) << endl; //Print-1
	cout << GetElem(L, 29) << endl; //Print 28 instructions correctly
}

Other operations of sequential storage are very simple. Next, you can try to realize all the operations you can think of.

3.3 implementation of linked storage structure (single linked list)

(Preface: LinkList L in this section is an LNode * type, which is an address. We need to change the value of L in the linked list function, so it should be linklist & L)

typedef struct LNode {
	ElemType data;
	struct LNode* next;
}LNode,* LinkList;			//LNode is the node and LinkList is the header pointer.
//It is equivalent to typedef int* LinkList. At this time, LinkList is a pointer to int data, which just replaces int with LNode

3.4 implementation of linked storage operation (single linked list)

3.4.1 establishing a single linked list by head interpolation: it is added to the chain header when adding elements.

/*
Establishing single linked list by head interpolation
*/
Status List_HeadInsert(LinkList &L){
	LNode* s=NULL;
	int e=9999;
	L = (LNode*)malloc(sizeof(LNode));//Create a header node, and the header pointer L points to the header node.
	if (!L) return ERROR;
	L->next = NULL;
	cin >> e ;
	while (e != 9999) {
		s = (LNode*)malloc(sizeof(LNode));//s is the new node
		if (!s) return ERROR;
		s->data = e;

		s->next = L->next;//The s node points to the previous node
		L->next = s;	  //s is always inserted after L
		cin >> e;
	}
	return OK;
}

In order to print a linear table, we write the same code

/*
Print linked list
*/
Status ListPrint(LinkList L) {
	LinkList p = L->next;				//Get header node
	while (p!= NULL) {
		cout << p->data ;
		cout << "\t";
		p = p->next;
	}
	cout << "\t" << endl;
	return OK;
}

int main() {
	LinkList L;
	List_HeadInsert(L);
	ListPrint(L);
}

The printing result is as follows:

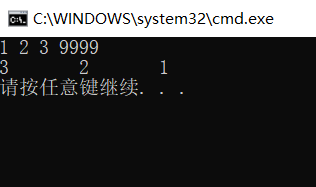
3.4.2 creating a single linked list by tail interpolation: add elements to the tail of the linked list when adding elements

/*
Establishing single linked list by tail interpolation
*/
Status List_TailInsert(LinkList& L) {
	LNode* s = NULL;
	LNode* r = NULL;
	int e = 9999;
	L = (LNode*)malloc(sizeof(LNode));
	if (!L) return ERROR;
	L->data = NULL;
	r = L;				//Tail interpolation requires r to assist
	cin >> e;
	while (e != 9999) {
		s = (LNode*)malloc(sizeof(LNode));//s is the new node
		s->data = e;

		s->next = NULL;
		r->next = s;	
		r = s;			//r is always the last node in the linked list
		cin >> e;
	}
	return OK;
}
int main() {
	LinkList L;
	//List_HeadInsert(L);
	List_TailInsert(L);
	ListPrint(L);
}

The printing results are as follows:

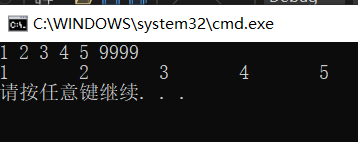
3.4.3 finding nodes by location (the same is true for finding nodes by location. You can try it yourself)

/*
Get the address of the ith location node
*/
LNode* GetElme(LinkList L, int i) {
	LNode *p = L->next;
	if (i < 1) return ERROR;
	i--;
	while (i > 0 && p!= NULL) {
		p = p->next;
		i--;
	}
	return p;
}
int main() {
	LinkList L;
	//List_HeadInsert(L);
	List_TailInsert(L);
	ListPrint(L);
	if(GetElme(L, 1)!=NULL)
		cout << GetElme(L, 1)->data << endl;
	if(GetElme(L, 5)==NULL)
		cout << ERROR << endl;
}

Print results:

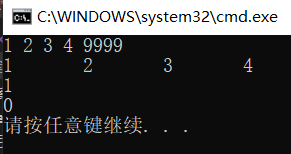
3.4.4 insert element at position i

/*
Insert element e at position i
*/
Status LinkListInsert(LinkList L, int i, ElemType e) {
	LNode* r = NULL;
	LNode* s = NULL;
	if (i == 1) r = L;
	else r = GetElme(L, i-1); //Get the previous node of the ith position

	if (r == NULL)
		return ERROR;		//If the previous node is NULL, i is illegal
	s = (LNode*)malloc(sizeof(LNode));
	if (!s) return ERROR;
	/*Insert node after node i-1*/
	s->data = e;
	s->next = r->next;
	r->next = s;

	return OK;
}
int main() {

	LinkList L;
	//List_HeadInsert(L);
	List_TailInsert(L);
	ListPrint(L);
	ElemType e = 9999;
	cin >> e;
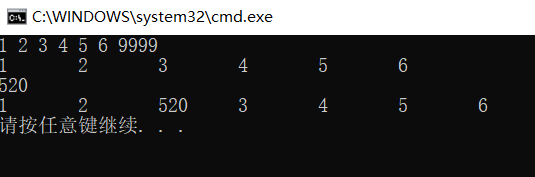
	LinkListInsert(L, 3, e);
	ListPrint(L);
}

The printing results are as follows: other methods, such as inserting in front of a node, can be tried by yourself.

3.4.5 deleting nodes

/*
Delete node i
*/
Status LinkListDelete(LinkList L, int i) {
	LNode* r = NULL;
	LNode* s = NULL;
	if (i == 1)
		r = L;
	else r = GetElme(L, i - 1);

	if (r == NULL) return ERROR;
	if (r->next == NULL) return ERROR;

	s = r->next;	
	r->next = s->next;
	free(s);
	return OK;
}
int main() {

	LinkList L;
	//List_HeadInsert(L);
	List_TailInsert(L);
	ListPrint(L);
	
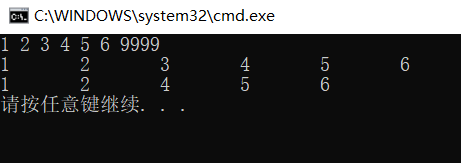
	LinkListDelete(L, 3);
	ListPrint(L);

}

Print results:

3.5 implementation of linear list - static linked list

3.5.1 physical structure of static linked list

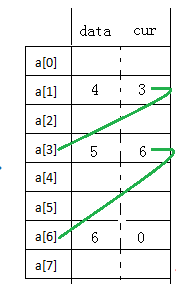
typedef struct{
	ElemType data;
	int cur;
}SLinkList[MaxSize];

Use the array to realize the function of linked list. The array element has a data field and a pointer field. The value of the pointer field is not the address, but the index of the next array element.

In fact, it is not as convenient as the linked list, but some high-level languages do not support pointers. This is a clever way to realize the linked list. Just learn this idea. If you have studied the operating system, you will also be familiar with this idea. The operation code about it is omitted, which is not important.

3.6 implementation of linear list - circular linked list

3.6.1 physical structure of circular linked list: we change the next of the last node of the linked list from NULL to the head node, and the whole linked list becomes a circle.

typedef struct LNode {
	ElemType data;
	struct LNode* next;
}LNode, * LinkList;

Yes, it's as like as two peas. In fact, there are differences when creating linked lists. Let's write the code of head interpolation and tail interpolation as follows:

3.7.2 as like as two peas, the first step is to build circular links.

Status RLinkList_HeadInsert(RLinkList& L) {
	int e = 9999;
	LNode* s = NULL;
	L = (LNode*)malloc(sizeof(LNode));
	if (!L) return ERROR;
	L->next =L;		//When there is no element, the header node points to itself instead of NULL 
	cin >> e;
	while (e != 9999) {
		s = (LNode*)malloc(sizeof(LNode));
		if (!s) return ERROR;
		s->data = e;

		s->next = L->next;
		L->next = s;
		cin >> e;
	}
	return OK;
}

3.7.3 tail insertion method to establish circular linked list: there is only one row left

Status RLinkList_TailInsert(RLinkList& L) {
	int e = 9999;
	LNode* s = NULL;
	LNode* r = NULL;
	L = (LNode*)malloc(sizeof(LNode));
	if (!L) return ERROR;
	L->next = L;	//When there is no element, the header node points to itself instead of NULL 
	r = L;
	cin >> e;
	while (e != 9999) {
		s = (LNode*)malloc(sizeof(LNode));
		if (!s) return ERROR;
		s->data = e;

		s->next = r->next;
		r->next = s;
		r = s;
		cin >> e;
	
	}
	return OK;
}

In order to verify, you also need to write and print a double linked list.

Status RLinkListPrint(RLinkList L) {
	LNode* p = L->next;
	while (p != L) { //Loop end condition changed
		cout << p->data;
		cout << "\t";
		p = p->next;
	}
	cout << "\t" << endl;
	return OK;
}

Let's try:

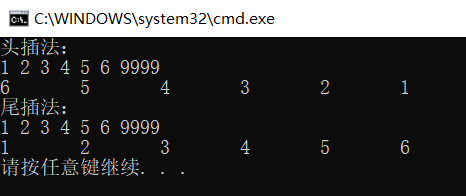
int main() {
	RLinkList L1 = NULL, L2 = NULL;
	cout << "Head insertion method:" << endl;
	RLinkList_HeadInsert(L1);
	RLinkListPrint(L1);
	cout << "Tail interpolation:" << endl;
	RLinkList_TailInsert(L2);
	RLinkListPrint(L2);
}

The printing results are as follows:

Other methods such as like as two peas and so on, and even the LinkList is changed to RLinkList.

3.7 implementation of linear list - double linked list

3.7.1 physical structure of double linked list: single linked list refers to one-way. We can only check the end of the single linked list from the head of the list. If we want to find the head of the chain from the end of the list, add another chain!

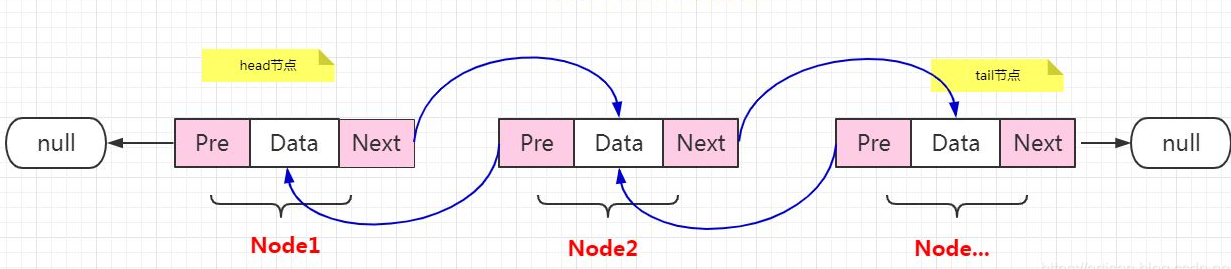
typedef struct LNode {
	ElemType data;
	struct LNode* next;//Successor pointer
	struct LNode* prior;//Precursor pointer
}LNode, * DLinkList;

Double tail insertion method:

Status DLinkList_HeadInsert(DLinkList &L){
	int e = 9999;
	LNode* s = NULL;
	L = (LNode*)malloc(sizeof(LNode));
	if (!L) return ERROR;
	L->next = NULL;
	L->prior = NULL; //One more "chain" has more steps than a single linked list
	cin >> e;
	while (e != 9999) {
		s = (LNode*)malloc(sizeof(LNode));
		s->data = e;

		L->next->prior = s; //The predecessor of the successor node points to more steps of the s node than the single linked list
		s->next = L->next;	//The successor of s points to its successor node
		s->prior = L;		//The precursor of s points to the L node 		   More steps than single linked list
		L->next = s;		//The successor of L points to the s node
		cin >> e;
	}
	return OK;
}
Status DLinkList_TailInser(DLinkList& L) {
	int e = 9999;
	LNode* s = NULL;
	LNode* r = NULL;
	L = (LNode*)malloc(sizeof(LNode));
	if (!L) return ERROR;
	L->next = NULL;
	L->prior = NULL; //One more "chain" has more steps than a single linked list
	r = L;
	cin >> e;
	while (e != 9999) {
		s = (LNode*)malloc(sizeof(LNode));
		s->data = e;

		L->next->prior = s; //The predecessor of the successor node points to more steps of the s node than the single linked list
		s->next = L->next;	//The successor of s points to its successor node
		s->prior = L;		//The precursor of s points to the L node 		   More steps than single linked list
		L->next = s;		//The successor of L points to the s node

		r = s;
		cin >> e;
	}
	return OK;
}

Write a print function. This print function can print both positive and negative!

Status ListPrint(DLinkList L, int reverse = 0) {
	DLinkList p = L->next;				//Get header node
	if (reverse == 1) {					//Reverse printing
		while (p->next != NULL)
			p = p->next;
		while (p != L) {
			cout << p->data;
			cout << "\t";
			p = p->prior;

		}
	}//if
	else {
		while (p != NULL) {
			cout << p->data;
			cout << "\t";
			p = p->next;
		}
	}//elese

	cout << "\t" << endl;
	return OK;
}

Then let's verify:

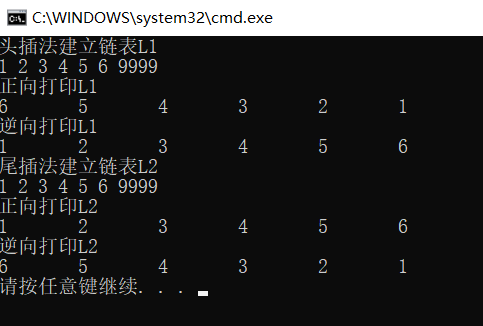
int main() {
	DLinkList L1 = NULL, L2 = NULL;
	cout << "Establishing linked list by head inserting method L1" << endl;
	DLinkList_HeadInsert(L1);
	cout << "Forward printing L1" << endl;
	ListPrint(L1);//The default is 0 forward printing
	cout << "Reverse printing L1" << endl;
	ListPrint(L1, 1);
	cout << "Tail insertion method to establish linked list L2" << endl;
	DLinkList_TailInsert(L2);
	cout << "Forward printing L2" << endl;
	ListPrint(L2);//The default is 0 forward printing
	cout << "Reverse printing L2" << endl;
	ListPrint(L2, 1);
}

The printing results are as follows:

3.7.3 operation by location

LNode* GetElem(DLinkList L, int i, int reverse = 0) {
	if (i < 1) return NULL;
	LNode*  p = L->next;
	i--;
	if (reverse != 1) {
		while (i > 0 && p != NULL) {
			p = p->next;
			i--;
		}//while
	}//if
	else {
		while (p->next != NULL && p != NULL)//Find the last node
			p = p->next;
		while (i > 0 && p != L) {
			p = p->prior;
			i--;
		}
	}
	return p;
}

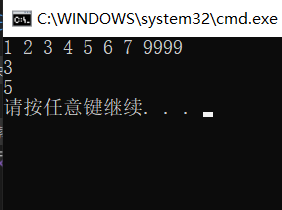
int main() {
	DLinkList L1 = NULL;
	DLinkList_TailInsert(L1);
	cout << GetElem(L1, 3)->data << endl;
	cout << GetElem(L1, 3,1)->data << endl;

}

The printing result is shown in the figure:

3.7.4 insertion operation

When inserting a node into a single linked list, you must first find the precursor of the node, and then insert it backward. Double linked list directly find i and insert it in front of it.

Status DLinkListInser(DLinkList L, int i, ElemType e) {
	LNode* l = GetElem(L, i);
	if (!l) return ERROR;
	LNode* s = (LNode*)malloc(sizeof(LNode));
	s->data = e;

	s->next = l;
	s->prior = l->prior;
	l->prior->next = s;
	l->prior = s;

	return OK;
}

Then let's verify:

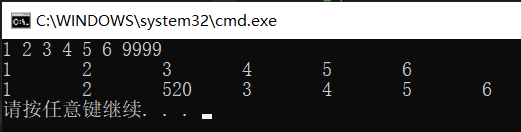
int main() {
	DLinkList L1 = NULL, L2 = NULL;
	DLinkList_TailInsert(L1);
	ListPrint(L1);
	DLinkListInser(L1, 3, 520);
	ListPrint(L1);

}

The printing results are as follows:

3.7.5 deleting elements

Status DLinkListDelete(DLinkList L, int i) {
	LNode* l = GetElem(L, i);
	if (!l) return ERROR;

	l->prior->next = l->next;
	if (l->next != NULL)
		l->next->prior = l;
	return OK;
}

Let's verify:

int main() {
	DLinkList L1 = NULL, L2 = NULL;
	DLinkList_TailInsert(L1);
	DLinkListDelete(L1, 3);
	ListPrint(L1);
}

Print results:

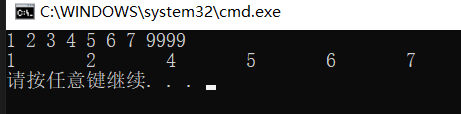
3.8 circular double linked list

3.8.1 the precursor of the physical structure head node points to the tail node, and the successor of the tail node points to the head node.

typedef struct LNode {
	ElemType data;
	struct LNode* next;
	struct LNode* prior;
}LNode, * RDLinkList;

The code is the same, but it's called RDLinkList. Why not DRLinkList, because I like it! The head interpolation and tail interpolation are only two rows away from the double linked list:

Status RDLinkList_HeadInsert(RDLinkList& L) {
	int e = 9999;
	LNode* s = NULL;
	L = (LNode*)malloc(sizeof(LNode));
	if (!L) return ERROR;
	L->next = L;	//It is only one row away from the two-way linked list
	L->prior = L;   //It is only one row away from the two-way linked list
	cin >> e;
	while (e != 9999) {
		s = (LNode*)malloc(sizeof(LNode));
		s->data = e;

		if (L->next != NULL) //When inserting the first node, there is no successor node
			L->next->prior = s;

		s->next = L->next;	//The successor of s points to its successor node
		s->prior = L;		//The precursor of s points to the L node 		   More steps than single linked list
		L->next = s;		//The successor of L points to the s node

		cin >> e;

	}
	return OK;
}

Status DLinkList_TailInsert(RDLinkList& L) {
	int e = 9999;
	LNode* s = NULL;
	LNode* r = NULL;
	L = (LNode*)malloc(sizeof(LNode));
	if (!L) return ERROR;
	L->next = L;//It is only one row away from the two-way linked list
	L->prior = L; //It is only one row away from the two-way linked list
	r = L;
	cin >> e;
	while (e != 9999) {
		s = (LNode*)malloc(sizeof(LNode));
		s->data = e;

		//No node after tail interpolation			
		s->next = r->next;	//The successor of s points to its successor node
		s->prior = r;		//The precursor of s points to the L node 		   More steps than single linked list
		r->next = s;		//The successor of L points to the s node

		r = s;
		cin >> e;
	}
	return OK;
}

Let's write a different printing function. It will print n nodes forward or backward.

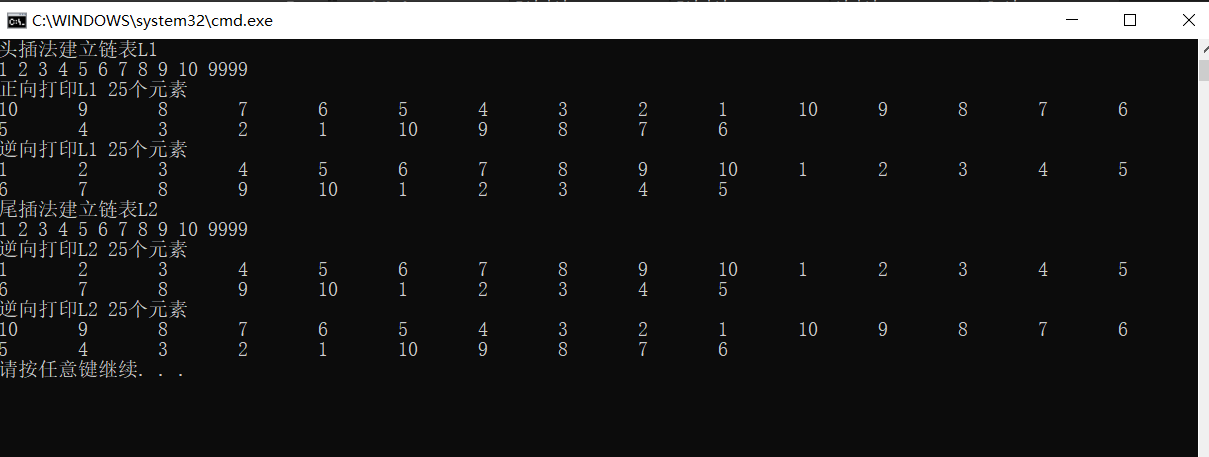
Other operations are as like as two peas linked lists. This is the end of the code implementation.

4. Summary and analysis

4.1 comparison between sequence list and linked list

Access mode: the sequential list can be accessed randomly, and the linked list can only access the elements from the beginning.

Logical structure and physical structure: when sequential storage is adopted, logically adjacent elements are also physically adjacent. When chain storage is adopted, logically adjacent elements are not necessarily physically adjacent.

Search, delete and insert operations: if you search by location, the time complexity of the sequence table = O(1), and the linked list = O(n).

Space allocation: the static allocation of the sequence table is prone to overflow. Excessive allocation may also waste space. It is difficult to grasp the size of the allocation value. In the dynamic allocation of sequence table, the element position needs to be moved every time it is reallocated, because the original continuous space may not meet the size of reallocated space, and the operation efficiency is low. The space allocation of linked list is very simple and flexible.

4.2 which physical structure to choose?

Based on storage considerations: when it is difficult to estimate the storage scale of linear tables, linked lists should be selected.

Based on the consideration of operation: if the search is frequent, the sequence table is a good choice. If you insert and delete frequently, linked list is a good choice.

Based on environmental considerations: some voice has no pointer, so we can't choose linked list.

To sum up, the stable linear table selects sequential storage, and the linear table with frequent insertion and deletion selects chain storage.

5. Exercises

(the answer to the exercise is: Linear table and exercise code)

Exercise 1

A single linked list with head node is known. Suppose that the linked list only gives the head pointer list without changing the linked list. Please design an algorithm as high as possible to find the node at the k position of the derivative in the linked list. k is an integer. If the search is successful, the algorithm outputs the value of the data field of the node and returns 1. Otherwise, it only returns 0.

Exercise 2

This topic is easy if you use the common idea of selective sorting, but the time is complex. The second is O(n^2). So think of one with less time complexity. Reminder: the same idea as exercise 1.

Exercise 3

Tip: all common methods need O(n^2) So think of an O(n) algorithm. You can consider trading space for time.

Exercise 4

The linked list is inverted in place. For the linked list L of the leading node, a space complexity of O(1) is designed, that is, the elements in the single linked list are inverted without the help of auxiliary space.

Exercise 5

Linear table L = (a1,a2,..., an), we design an algorithm with spatial complexity O(1), and change linear table l into L=(a1,an,a2,an-1,...).

The time complexity of our answer is no more than O(n).

Keywords: C++ data structure linked list

Added by pfoger on Thu, 10 Mar 2022 11:11:11 +0200

Programming VIP

System master data structure 3 linear table C + + implementation

1. Logical structure

2. Storage structure

2.1 sequential storage

2.2 chain storage

3. Implementation of linear table

3.1 implementation of sequential storage structure

3.2 implementation of sequential storage operation

3.3 implementation of linked storage structure (single linked list)

3.4 implementation of linked storage operation (single linked list)

3.5 implementation of linear list - static linked list

3.6 implementation of linear list - circular linked list

3.7 implementation of linear list - double linked list

3.8 circular double linked list

4. Summary and analysis

5. Exercises

Popular Keywords