abstract

This paper introduces the mark sweep algorithm, which focuses on pointer inversion. Supplement the anti fragmentation cleaning in the exercise. Copy, concurrency and other exercises to be supplemented. But the algorithm is a little old. I feel that the bit trick of the semi numerical algorithm in Volume II may be better.

data structure

Gartner uses the data structure of tree to represent tables in TAOCP. (trick: we can build each table that is active at the same time as a tree, and use the anonymous root node as the root of all trees, then the tree of the whole program will be established).

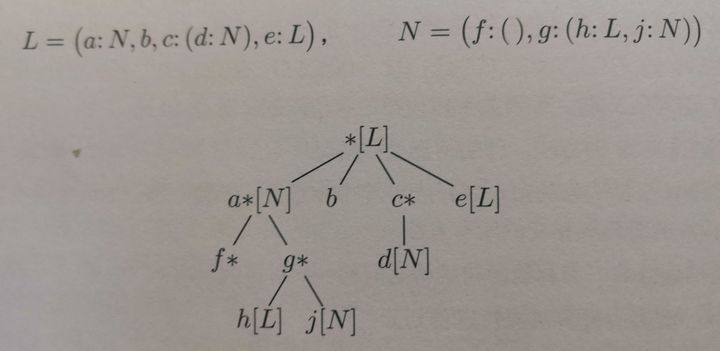
The concept of table is complex. We can understand it as a structure.

However, Knuth does not use a multi fork data structure, but allows each node to contain lhs and rhs pointers. (the main problem is that Knuth introduced multi chain structure after writing GC!!! Anti human)

In addition, the header of each table is a node whose lhs is empty

The rhs of the node points to the next non atomic node.

lhs of nodes can be divided into three situations:

The node is like sturct - > points to the header of the child table

Node is a value (like int) - > pointing to atomic node (before Knuth modification, direct data + rhs)

A node is a pointer (like struct *) - > pointing to other nodes

There is only data in the atomic node (direct data + RHS before Knuth modification)

In this way, the original GC of the graph becomes a spanning tree + back edge + forward edge + cross edge. However, there is a special point, which is different from the ordinary spanning tree. Because only lhs and rhs can be pointed out here, the degree is < = 2. This is also a benefit of this data structure.

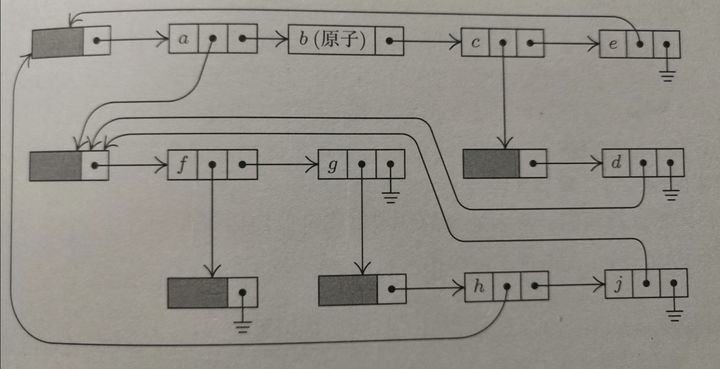
Note that knuth has been modified later. There is no rhs in the atomic node. I vomited!!!!!!!!!!

Mark sweep GC

Mark sweep GC is divided into two stages:

Start traversing from the nodes that can be accessed by the main program and mark the reachable nodes

Traverse the memory pool sequentially and clear unreachable nodes

There are some important changes in the second stage, which I mentioned in the EX part, mainly related to anti fragmentation.

The first phase is Knuth's focus.

Obviously, the first stage is a DFS algorithm.

Question 1: DFS recursion depth is too large

Ans 1: use explicit stack

Question 2: GC is usually performed when there is little free memory, and the memory is still insufficient

Ans 2: do not use the auxiliary stack space, record the stack information in the node (temporarily destroy the table structure) Deutsch

We directly introduce a relatively excellent algorithm recommended by Knuth. Of course, there are also variants in modern times.

Marking algorithm

One sentence summary: store stack information in the node and recover it during backtracking

We assume that a node consists of four fields, which is also a difficulty of GC, because GC needs the least memory overhead and can only use a small amount of storage.

• mark
• atom (if it is not an atomic node, it is used to mark the backtracking process belonging to lhs or rhs)
• lhs
• rhs

The atomic node does not have lhs/rhs. These fields are used to store other data (the size is not necessarily two pointers). It can be considered that the atomic node is a leaf node

Rewrite the author's pseudo code in C style, and the results are as follows.

INIT:
pre = nullptr, cur = p0;
MARK:
p->mark = true;
CHECK:
if(cur->atom)
 goto TRACEBACK;
LHS:
next = cur->lhs;
if(next && !next->mark){
  cur->atom = true;
  cur->lhs = pre;
  pre = cur;
  cur = next;
  goto MARK;
}
RHS:
next = cur->rhs;
if(next && !next->mark){
  cur->rhs = pre;
  pre = cur;
  cur = next;
  goto MARK;
}
TRACEBACK:
if(!pre) return;
next = pre;
if(next->atom){
  next->atom = false;
  pre = next-> lhs;
  next-> lhs = cur;
  cur = next;
  goto RHS;
}
else{
  pre = next-> rhs;
  next-> rhs = cur;
  cur = next;
  goto TRACEBACK;
}

analyse

INIT PHASE

INIT:
pre = nullptr, cur = p0;

Here, pre represents the top node of the stack and cur represents the current node.

MARK PHASE

MARK:
p->mark = true;

Mark current node reachable

CHECK PHASE

CHECK:
if(cur->atom)
 goto TRACEBACK;

If the atomic node, immediately trace back to the previous node. Because the atomic node does not have lhs/rhs

It is impossible that the change of lhs causes atom, because if cur has marked and accessed lhs, it will not enter the mark phase above. It can only be after backtracking, but atom will be reset during backtracking, so it is impossible.

LHS PHASE

LHS:
next = cur->lhs;
if(next && !next->mark){
  cur->atom = true;
  cur->lhs = pre;
  pre = cur;
  cur = next;
  goto MARK;
}

Mark atom as true to tell TRACEBACK that the current stack information is stored in the left node.

lhs stores the previous top of the stack, puts the current cur on the stack (in fact, the stack is just an element), and then accesses the next node. Similar to DFS, the difference is that the previous top of the stack is stored in lhs.

goto MARK； Depth first

RHS PHASE

RHS:
next = cur->rhs;
if(next && !next->mark){
  cur->rhs = pre;
  pre = cur;
  cur = next;
  goto MARK;
}

The difference is that atom is not marked as true. Because the above condition can be established only after the left node of the current node has been traversed.

In the previous backtracking process, we set the atom of the fallback node to false to restore its lhs. Therefore, keep atom false here to let TRACEBACK know. The next step is to backtrack from the right node.

TRACEBACK:
...
next->atom = false;

TRACEBACK PHASE

TRACEBACK:
if(!pre) return;
next = pre;
if(next->atom){
  next->atom = false;
  pre = next-> lhs;
  next-> lhs = cur;
  cur = next;
  goto RHS;
}
else{
  pre = next-> rhs;
  next-> rhs = cur;
  cur = next;
  goto TRACEBACK;
}

if(!pre) indicates that you have fallen back to the starting node. Obviously DFS is over.

next = pre is equivalent to the top of pop stack.

If the previous node atom (lhs is modified), restore its lhs, goto RHS, and traverse the right node of the previous node.

If the previous node! atom, restore its rhs and goto TRACEBACK (because the left node of the previous node must have traversed first)

Extension

Ex 5[Schorr and Waite]CACM 10(1967),501-506

At the same time, the auxiliary stack is used. The node is used to store stack information only when the stack is full. When godner wrote the first volume, this algorithm was the best algorithm at that time.

Ex 9 [Daniel Edwards]

Anti fragmentation algorithm

One sentence summary: when cleaning, replace all the active memory to the front, and leave information at the original address so that the pointer to the active memory can be correctly switched to the new memory

There are memory blocks in the original memory pool

. Reorganize the marked nodes so that all marked nodes are

. If necessary, change the lhs and rhs of non atomic fields to maintain the table structure.

The pointers above all point to a node, so we use. Instead of - >

INIT:
i=0； k=m+1;
FIRSTUSE:
while(node[++i].mark);
LASTFREE:
while(!node[--k].mark);
SWAP:
if(i>k)
goto MAINTAIN;
else
node[i]=node[k]
node[k].lhs = node+i;
node[k].mark = false;
goto FIRSTUSE;
MAINTAIN:
for i from 1 to k
node[k].mark=false;
if(!node[i].atom && node[k].lhs > node+k)
node[i].lhs = node[i].lhs->lhs;
if(!node[i].atom && node[k].rhs > node+k)
node[i].lhs = node[i].rhs->lhs;

analyse

INIT PHASE

INIT:
i=0； k=m+1;

Initialize header and footer indexes

FISRTUSE/LASTFREE PHASE

FIRSTUSE:
while(node[++i].mark);
LASTFREE:
while(!node[--k].mark);

i is the first free memory block

k is the last active memory block

SWAP PHASE

SWAP:
if(i>k)
goto MAINTAIN;
else
node[i]=node[k]
node[k].lhs = node+i;
node[k].mark = false;
goto FIRSTUSE;

Overwrite the active memory on the free memory, and recover the mark for the next GC.

Now the original active memory can be free, but because there was a pointer to this active area before, we must leave information so that the previous pointer can correctly point to the changed area. (MOST TRICKY!!!!)

Therefore, we set lhs to node+i, that is, the changed address

If I > k, all free blocks are exchanged to the last active block. At this time, both free and active blocks are continuous

MAINTAIN PHASE

MAINTAIN:
for i from 1 to k
node[i].mark=false;
if(!node[i].atom && node[i].lhs > node+k)
node[i].lhs = node[i].lhs->lhs;
if(!node[i].atom && node[i].rhs > node+k)
node[i].rhs = node[i].rhs->lhs;

Restore the mark s of all active block s

If it is an atomic node, you do not need to restore lhs rhs, because lhs/rhs is not a pointer field

If the pointer points after node+k (that is, the free area), it indicates that the block pointed to has undergone swap

Then, according to the changed address we saved in lhs, we restore the pointer to the active block it should point to