Task 07: advanced optimization algorithm; word2vec; advanced word embedding

Task07: advanced optimization algorithm; word2vec; advanced word embedding

1. Advanced optimization algorithm

Momentum

In Section 11.4, we mentioned that the gradient of the objective function with respect to the independent variable represents the direction in which the objective function declines fastest at the current position of the independent variable. Therefore, gradient descent is also called the steepest descent. In each iteration, the gradient descent updates the independent variable along the gradient of the current position according to the current position of the independent variable. However, if the iteration direction of an independent variable only depends on the current position of the independent variable, this may cause some problems. For noisy gradient, we need to carefully select the learning rate and batch size to control the gradient variance and convergence results.

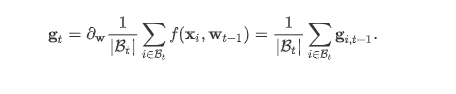
Supp: Preconditioning

exponential moving average

Realization:

def get_data_ch7():  
    data = np.genfromtxt('/home/kesci/input/airfoil4755/airfoil_self_noise.dat', delimiter='\t')
    data = (data - data.mean(axis=0)) / data.std(axis=0)
    return torch.tensor(data[:1500, :-1], dtype=torch.float32), \
        torch.tensor(data[:1500, -1], dtype=torch.float32)

features, labels = get_data_ch7()

def init_momentum_states():
    v_w = torch.zeros((features.shape[1], 1), dtype=torch.float32)
    v_b = torch.zeros(1, dtype=torch.float32)
    return (v_w, v_b)

def sgd_momentum(params, states, hyperparams):
    for p, v in zip(params, states):
        v.data = hyperparams['momentum'] * v.data + hyperparams['lr'] * p.grad.data
        p.data -= v.data

d2l.train_ch7(sgd_momentum, init_momentum_states(),
              {'lr': 0.02, 'momentum': 0.5}, features, labels)

d2l.train_ch7(sgd_momentum, init_momentum_states(),
              {'lr': 0.02, 'momentum': 0.9}, features, labels)
              
d2l.train_ch7(sgd_momentum, init_momentum_states(),
              {'lr': 0.004, 'momentum': 0.9}, features, labels)

d2l.train_pytorch_ch7(torch.optim.SGD, {'lr': 0.004, 'momentum': 0.9},
                    features, labels)

AdaGrad

%matplotlib inline
import math
import torch
import sys
sys.path.append("/home/kesci/input") 
import d2lzh1981 as d2l

def adagrad_2d(x1, x2, s1, s2):
    g1, g2, eps = 0.2 * x1, 4 * x2, 1e-6  # The first two terms are independent variable gradients
    s1 += g1 ** 2
    s2 += g2 ** 2
    x1 -= eta / math.sqrt(s1 + eps) * g1
    x2 -= eta / math.sqrt(s2 + eps) * g2
    return x1, x2, s1, s2

def f_2d(x1, x2):
    return 0.1 * x1 ** 2 + 2 * x2 ** 2

def get_data_ch7():  
    data = np.genfromtxt('/home/kesci/input/airfoil4755/airfoil_self_noise.dat', delimiter='\t')
    data = (data - data.mean(axis=0)) / data.std(axis=0)
    return torch.tensor(data[:1500, :-1], dtype=torch.float32), \
        torch.tensor(data[:1500, -1], dtype=torch.float32)
        
features, labels = get_data_ch7()

def init_adagrad_states():
    s_w = torch.zeros((features.shape[1], 1), dtype=torch.float32)
    s_b = torch.zeros(1, dtype=torch.float32)
    return (s_w, s_b)

def adagrad(params, states, hyperparams):
    eps = 1e-6
    for p, s in zip(params, states):
        s.data += (p.grad.data**2)
        p.data -= hyperparams['lr'] * p.grad.data / torch.sqrt(s + eps)

d2l.train_ch7(adagrad, init_adagrad_states(), {'lr': 0.1}, features, labels)

RMSProp

%matplotlib inline
import math
import torch
import sys
sys.path.append("/home/kesci/input") 
import d2lzh1981 as d2l

def rmsprop_2d(x1, x2, s1, s2):
    g1, g2, eps = 0.2 * x1, 4 * x2, 1e-6
    s1 = beta * s1 + (1 - beta) * g1 ** 2
    s2 = beta * s2 + (1 - beta) * g2 ** 2
    x1 -= alpha / math.sqrt(s1 + eps) * g1
    x2 -= alpha / math.sqrt(s2 + eps) * g2
    return x1, x2, s1, s2

def f_2d(x1, x2):
    return 0.1 * x1 ** 2 + 2 * x2 ** 2
alpha, beta = 0.4, 0.9
d2l.show_trace_2d(f_2d, d2l.train_2d(rmsprop_2d))


def get_data_ch7():  
    data = np.genfromtxt('/home/kesci/input/airfoil4755/airfoil_self_noise.dat', delimiter='\t')
    data = (data - data.mean(axis=0)) / data.std(axis=0)
    return torch.tensor(data[:1500, :-1], dtype=torch.float32), \
        torch.tensor(data[:1500, -1], dtype=torch.float32)
        
features, labels = get_data_ch7()

def init_rmsprop_states():
    s_w = torch.zeros((features.shape[1], 1), dtype=torch.float32)
    s_b = torch.zeros(1, dtype=torch.float32)
    return (s_w, s_b)

def rmsprop(params, states, hyperparams):
    gamma, eps = hyperparams['beta'], 1e-6
    for p, s in zip(params, states):
        s.data = gamma * s.data + (1 - gamma) * (p.grad.data)**2
        p.data -= hyperparams['lr'] * p.grad.data / torch.sqrt(s + eps)

d2l.train_ch7(rmsprop, init_rmsprop_states(), {'lr': 0.01, 'beta': 0.9},
              features, labels)

AdaDelta

Realization:

def init_adadelta_states():
    s_w, s_b = torch.zeros((features.shape[1], 1), dtype=torch.float32), torch.zeros(1, dtype=torch.float32)
    delta_w, delta_b = torch.zeros((features.shape[1], 1), dtype=torch.float32), torch.zeros(1, dtype=torch.float32)
    return ((s_w, delta_w), (s_b, delta_b))

def adadelta(params, states, hyperparams):
    rho, eps = hyperparams['rho'], 1e-5
    for p, (s, delta) in zip(params, states):
        s[:] = rho * s + (1 - rho) * (p.grad.data**2)
        g =  p.grad.data * torch.sqrt((delta + eps) / (s + eps))
        p.data -= g
        delta[:] = rho * delta + (1 - rho) * g * g

d2l.train_ch7(adadelta, init_adadelta_states(), {'rho': 0.9}, features, labels)

d2l.train_pytorch_ch7(torch.optim.Adadelta, {'rho': 0.9}, features, labels)

Adam

%matplotlib inline
import torch
import sys
sys.path.append("/home/kesci/input") 
import d2lzh1981 as d2l

def get_data_ch7():  
    data = np.genfromtxt('/home/kesci/input/airfoil4755/airfoil_self_noise.dat', delimiter='\t')
    data = (data - data.mean(axis=0)) / data.std(axis=0)
    return torch.tensor(data[:1500, :-1], dtype=torch.float32), \
        torch.tensor(data[:1500, -1], dtype=torch.float32)
        
features, labels = get_data_ch7()

def init_adam_states():
    v_w, v_b = torch.zeros((features.shape[1], 1), dtype=torch.float32), torch.zeros(1, dtype=torch.float32)
    s_w, s_b = torch.zeros((features.shape[1], 1), dtype=torch.float32), torch.zeros(1, dtype=torch.float32)
    return ((v_w, s_w), (v_b, s_b))

def adam(params, states, hyperparams):
    beta1, beta2, eps = 0.9, 0.999, 1e-6
    for p, (v, s) in zip(params, states):
        v[:] = beta1 * v + (1 - beta1) * p.grad.data
        s[:] = beta2 * s + (1 - beta2) * p.grad.data**2
        v_bias_corr = v / (1 - beta1 ** hyperparams['t'])
        s_bias_corr = s / (1 - beta2 ** hyperparams['t'])
        p.data -= hyperparams['lr'] * v_bias_corr / (torch.sqrt(s_bias_corr) + eps)
    hyperparams['t'] += 1
d2l.train_ch7(adam, init_adam_states(), {'lr': 0.01, 't': 1}, features, labels)

d2l.train_pytorch_ch7(torch.optim.Adam, {'lr': 0.01}, features, labels)

2.word2vec

We use one hot vectors to represent words in the section of "implementation of cyclic neural networks from scratch". Although they are easy to construct, they are not usually a good choice. One of the main reasons is that one hot word vector can not accurately express the similarity between different words, such as cosine similarity which we often use.

Word2Vec word embedding tool is proposed to solve the above problem. It represents each word as a fixed length vector, and through the pre training on corpus, these vectors can better express the similarity and analogy between different words, so as to introduce certain semantic information. Based on the assumption of two probability models, we can define two Word2Vec models:

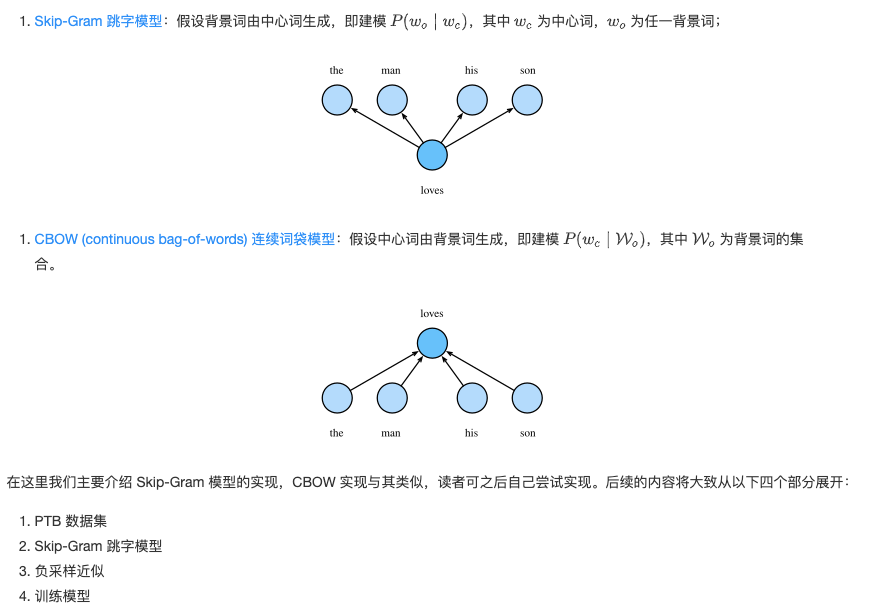
PTB data set

In short, Word2Vec can learn from the corpus how to map discrete words into vectors in continuous space, and retain their semantic similarity. So in order to train Word2Vec model, we need a natural language corpus, from which we will learn the relationship between words. Here we use the classic PTB corpus for training. PTB (Penn Tree Bank) is a commonly used small corpus, which samples articles from the Wall Street Journal, including training set, verification set and test set. We will train the word embedding model on the PTB training set.

Load data set

with open('/home/kesci/input/ptb_train1020/ptb.train.txt', 'r') as f:
    lines = f.readlines() # The sentences in the dataset are divided by line breaks
    raw_dataset = [st.split() for st in lines] # st is the abbreviation of sentence. The words are divided by spaces
print('# sentences: %d' % len(raw_dataset))

# For the first three sentences in the dataset, print the number of words in each sentence and the first five words
# At the end of the sentence is' ', all the strange words are represented by' ', and the number is replaced by' N '
for st in raw_dataset[:3]:
    print('# tokens:', len(st), st[:5])

Index words

counter = collections.Counter([tk for st in raw_dataset for tk in st]) # tk is the abbreviation of token
counter = dict(filter(lambda x: x[1] >= 5, counter.items())) # Keep only words that appear at least five times in the dataset

idx_to_token = [tk for tk, _ in counter.items()]
token_to_idx = {tk: idx for idx, tk in enumerate(idx_to_token)}
dataset = [[token_to_idx[tk] for tk in st if tk in token_to_idx]
           for st in raw_dataset] # The words in raw? Dataset are converted to corresponding idx in this step
num_tokens = sum([len(st) for st in dataset])
'# tokens: %d' % num_tokens

Two sampling

def discard(idx):
    '''
    @params:
        idx: Subscripts of words
    @return: True/False Indicates whether to discard the word
    '''
    return random.uniform(0, 1) < 1 - math.sqrt(
        1e-4 / counter[idx_to_token[idx]] * num_tokens)

subsampled_dataset = [[tk for tk in st if not discard(tk)] for st in dataset]
print('# tokens: %d' % sum([len(st) for st in subsampled_dataset]))

def compare_counts(token):
    return '# %s: before=%d, after=%d' % (token, sum(
        [st.count(token_to_idx[token]) for st in dataset]), sum(
        [st.count(token_to_idx[token]) for st in subsampled_dataset]))

print(compare_counts('the'))
print(compare_counts('join'))

Extract the center word and background word

def get_centers_and_contexts(dataset, max_window_size):
    '''
    @params:
        dataset: The data set is the set of sentences, and each sentence is the set of words. At this time, the words have been converted into corresponding number subscripts
        max_window_size: Maximum window size of background words
    @return:
        centers: Set of central words
        contexts: The set of background word window corresponds to the center word, and each background word window is the set of background words
    '''
    centers, contexts = [], []
    for st in dataset:
        if len(st) < 2:  # Each sentence must have at least two words to form a pair of "center word background words"
            continue
        centers += st
        for center_i in range(len(st)):
            window_size = random.randint(1, max_window_size) # Random selection of background word window size
            indices = list(range(max(0, center_i - window_size),
                                 min(len(st), center_i + 1 + window_size)))
            indices.remove(center_i)  # Exclude the center word from the background word
            contexts.append([st[idx] for idx in indices])
    return centers, contexts

all_centers, all_contexts = get_centers_and_contexts(subsampled_dataset, 5)

tiny_dataset = [list(range(7)), list(range(7, 10))]
print('dataset', tiny_dataset)
for center, context in zip(*get_centers_and_contexts(tiny_dataset, 2)):
    print('center', center, 'has contexts', context)

Skip gram model

embed = nn.Embedding(num_embeddings=10, embedding_dim=4)
print(embed.weight)

x = torch.tensor([[1, 2, 3], [4, 5, 6]], dtype=torch.long)
print(embed(x))


X = torch.ones((2, 1, 4))
Y = torch.ones((2, 4, 6))
print(torch.bmm(X, Y).shape


def skip_gram(center, contexts_and_negatives, embed_v, embed_u):
    '''
    @params:
        center: Center word subscript, shape is (n, 1) Integral tensor of
        contexts_and_negatives: Subscripts of background words and noise words in the form of (n, m) Integral tensor of
        embed_v: Central word embedding layer
        embed_u: Background words embedding layer
    @return:
        pred: The inner product of the center word and the background word (or noise word), which can then be used to calculate the probability p(w_o|w_c)
    '''
    v = embed_v(center) # shape of (n, 1, d)
    u = embed_u(contexts_and_negatives) # shape of (n, m, d)
    pred = torch.bmm(v, u.permute(0, 2, 1)) # bmm((n, 1, d), (n, d, m)) => shape of (n, 1, m)
    return pred

Negative sampling approximation

def get_negatives(all_contexts, sampling_weights, K):
    '''
    @params:
        all_contexts: [[w_o1, w_o2, ...], [...], ... ]
        sampling_weights: Sampling probability of noise words per word
        K: Number of random samples
    @return:
        all_negatives: [[w_n1, w_n2, ...], [...], ...]
    '''
    all_negatives, neg_candidates, i = [], [], 0
    population = list(range(len(sampling_weights)))
    for contexts in all_contexts:
        negatives = []
        while len(negatives) < len(contexts) * K:
            if i == len(neg_candidates):
                # According to the weight of each word, the index of k words is randomly generated as noise words.
                # For efficient calculation, k can be set a little larger
                i, neg_candidates = 0, random.choices(
                    population, sampling_weights, k=int(1e5))
            neg, i = neg_candidates[i], i + 1
            # Noise words cannot be background words
            if neg not in set(contexts):
                negatives.append(neg)
        all_negatives.append(negatives)
    return all_negatives

sampling_weights = [counter[w]**0.75 for w in idx_to_token]
all_negatives = get_negatives(all_contexts, sampling_weights, 5)

class MyDataset(torch.utils.data.Dataset):
    def __init__(self, centers, contexts, negatives):
        assert len(centers) == len(contexts) == len(negatives)
        self.centers = centers
        self.contexts = contexts
        self.negatives = negatives
        
    def __getitem__(self, index):
        return (self.centers[index], self.contexts[index], self.negatives[index])

    def __len__(self):
        return len(self.centers)
    
def batchify(data):
    '''
    //Use as parameter collate for DataLoader
    @params:
        data: Chang Wei batch_size Each element in the list is__getitem__Results obtained
    @outputs:
        batch: Obtained after batching (centers, contexts_negatives, masks, labels) tuple
            centers: Center word subscript, shape is (n, 1) Integral tensor of
            contexts_negatives: Subscripts of background words and noise words in the form of (n, m) Integral tensor of
            masks: Mask corresponding to complement, shape is (n, m) 0/1 Integer tensor
            labels: Label indicating the central word in the form of (n, m) 0/1 Integer tensor
    '''
    max_len = max(len(c) + len(n) for _, c, n in data)
    centers, contexts_negatives, masks, labels = [], [], [], []
    for center, context, negative in data:
        cur_len = len(context) + len(negative)
        centers += [center]
        contexts_negatives += [context + negative + [0] * (max_len - cur_len)]
        masks += [[1] * cur_len + [0] * (max_len - cur_len)] # The mask variable mask is used to avoid the influence of the filled item on the loss function calculation
        labels += [[1] * len(context) + [0] * (max_len - len(context))]
        batch = (torch.tensor(centers).view(-1, 1), torch.tensor(contexts_negatives),
            torch.tensor(masks), torch.tensor(labels))
    return batch

batch_size = 512
num_workers = 0 if sys.platform.startswith('win32') else 4

dataset = MyDataset(all_centers, all_contexts, all_negatives)
data_iter = Data.DataLoader(dataset, batch_size, shuffle=True,
                            collate_fn=batchify, 
                            num_workers=num_workers)
for batch in data_iter:
    for name, data in zip(['centers', 'contexts_negatives', 'masks',
                           'labels'], batch):
        print(name, 'shape:', data.shape)
    break


class SigmoidBinaryCrossEntropyLoss(nn.Module):
    def __init__(self):
        super(SigmoidBinaryCrossEntropyLoss, self).__init__()
    def forward(self, inputs, targets, mask=None):
        '''
        @params:
            inputs: after sigmoid Forecast after layer D=1 Probability
            targets: 0/1 Vector, 1 for background word, 0 for noise word
        @return:
            res: Average to each label Of loss
        '''
        inputs, targets, mask = inputs.float(), targets.float(), mask.float()
        res = nn.functional.binary_cross_entropy_with_logits(inputs, targets, reduction="none", weight=mask)
        res = res.sum(dim=1) / mask.float().sum(dim=1)
        return res

loss = SigmoidBinaryCrossEntropyLoss()

pred = torch.tensor([[1.5, 0.3, -1, 2], [1.1, -0.6, 2.2, 0.4]])
label = torch.tensor([[1, 0, 0, 0], [1, 1, 0, 0]]) # 1 and 0 in label variables represent background words and noise words respectively
mask = torch.tensor([[1, 1, 1, 1], [1, 1, 1, 0]])  # Mask variable
print(loss(pred, label, mask))

def sigmd(x):
    return - math.log(1 / (1 + math.exp(-x)))
print('%.4f' % ((sigmd(1.5) + sigmd(-0.3) + sigmd(1) + sigmd(-2)) / 4)) # Note that 1-sigmoid(x) = sigmoid(-x)
print('%.4f' % ((sigmd(1.1) + sigmd(-0.6) + sigmd(-2.2)) / 3))



embed_size = 100
net = nn.Sequential(nn.Embedding(num_embeddings=len(idx_to_token), embedding_dim=embed_size),
                    nn.Embedding(num_embeddings=len(idx_to_token), embedding_dim=embed_size))


    device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
    print("train on", device)
    net = net.to(device)
    optimizer = torch.optim.Adam(net.parameters(), lr=lr)
    for epoch in range(num_epochs):
        start, l_sum, n = time.time(), 0.0, 0
        for batch in data_iter:
            center, context_negative, mask, label = [d.to(device) for d in batch]
            
            pred = skip_gram(center, context_negative, net[0], net[1])
            
            l = loss(pred.view(label.shape), label, mask).mean() # The average loss of a batch
            optimizer.zero_grad()
            l.backward()
            optimizer.step()
            l_sum += l.cpu().item()
            n += 1
        print('epoch %d, loss %.2f, time %.2fs'
              % (epoch + 1, l_sum / n, time.time() - start))

train(net, 0.01, 5)



def get_similar_tokens(query_token, k, embed):
    '''
    @params:
        query_token: Given words
        k: The number of synonyms
        embed: Pre training word vector
    '''
    W = embed.weight.data
    x = W[token_to_idx[query_token]]
    # 1e-9 is added for numerical stability
    cos = torch.matmul(W, x) / (torch.sum(W * W, dim=1) * torch.sum(x * x) + 1e-9).sqrt()
    _, topk = torch.topk(cos, k=k+1)
    topk = topk.cpu().numpy()
    for i in topk[1:]:  # Remove input word
        print('cosine sim=%.3f: %s' % (cos[i], (idx_to_token[i])))
        
get_similar_tokens('chip', 3, net[0])

3. Advanced word embedding

GloVe model

KNN for synonyms

def knn(W, x, k):
    '''
    @params:
        W: Set of all vectors
        x: Orientated quantity
        k: Number of queries
    @outputs:
        topk: Maximum cosine similarity k Subscript per subscript
        [...]: cosine similarity 
    '''
    cos = torch.matmul(W, x.view((-1,))) / (
        (torch.sum(W * W, dim=1) + 1e-9).sqrt() * torch.sum(x * x).sqrt())
    _, topk = torch.topk(cos, k=k)
    topk = topk.cpu().numpy()
    return topk, [cos[i].item() for i in topk]

def get_similar_tokens(query_token, k, embed):
    '''
    @params:
        query_token: Given word
        k: The number of synonyms needed
        embed: Pre training word vector
    '''
    topk, cos = knn(embed.vectors,
                    embed.vectors[embed.stoi[query_token]], k+1)
    for i, c in zip(topk[1:], cos[1:]):  # Remove input word
        print('cosine sim=%.3f: %s' % (c, (embed.itos[i])))

get_similar_tokens('chip', 3, glove)


def get_analogy(token_a, token_b, token_c, embed):
    '''
    @params:
        token_a: Word a
        token_b: Word b
        token_c: Word c
        embed: Pre training word vector
    @outputs:
        res: Analogical words d
    '''
    vecs = [embed.vectors[embed.stoi[t]] 
                for t in [token_a, token_b, token_c]]
    x = vecs[1] - vecs[0] + vecs[2]
    topk, cos = knn(embed.vectors, x, 1)
    res = embed.itos[topk[0]]
    return res

get_analogy('man', 'woman', 'son', glove)

reference:
https://www.kesci.com/org/boyuai/project/5e47c7ac17aec8002dc5652a
https://www.kesci.com/org/boyuai/project/5e48088d17aec8002dc5f4ab
https://www.kesci.com/org/boyuai/project/5e48089f17aec8002dc5f4d0

StarCoder_Yue

38 original articles published, 24 praised, 40000 visitors+

Private letter follow

Keywords: Lambda

Added by n14charlie on Tue, 25 Feb 2020 08:47:29 +0200

Programming VIP

Task 07: advanced optimization algorithm; word2vec; advanced word embedding