Abstract: given a connected undirected graph, ask how many points must be deleted at least to make the two points s,t disconnected.
According to the minimum cut theorem of maximum flow, we can obtain the minimum cut of S - > t by finding the maximum flow of S - > t, but the cut is an edge set rather than a point set. Therefore, we need to convert point cut to edge cut.

In the solution of a rogue problem: the graph of interested lsy users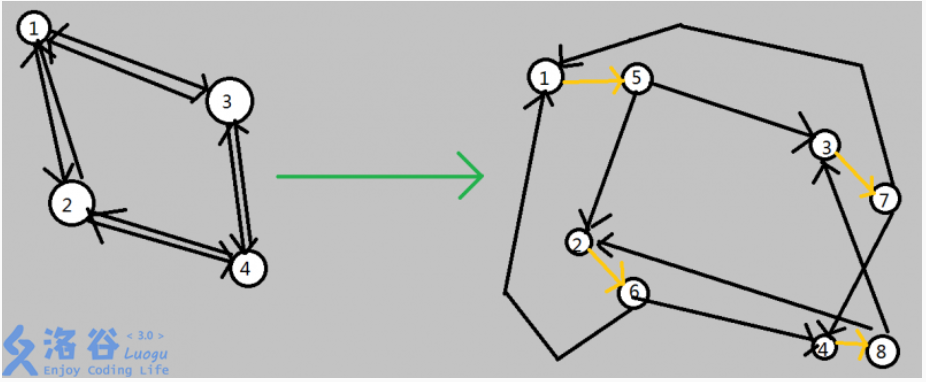
Each point is divided into two points, one is the entry point of the point (that is, the edge pointing to the point in the original image now points to the point), the other is the exit point of the point (that is, the exit edge of the point in the original image now points out through the point), and then a directed edge is added between the entry point and the exit point. In this way, the edge of each point is unique. Cutting this edge is equivalent to cutting this point (because other connected points can't go through, which is the same as deleting this point), so it can be converted into edge cutting set.
About building a graph: it can be observed that the undirected graph is processed into a directed graph in this way, and the outgoing edge in the original graph is not affected. Therefore, the outgoing edge capacity is set to INF, and the yellow edge (i.e. the newly added incoming edge) capacity is set to 1. Just run with the network flow algorithm.

About the starting point of the algorithm: after this processing, we can't take the origin s as the starting point, because the s point now only has an outgoing edge with a capacity of 1, so we can't run the maximum flow. We should take the outgoing point of s as the starting point, and the edge connecting the outgoing points is the outgoing edge of the s point in the original graph, with a capacity of INF.

#include<bits/stdc++.h>
using namespace std;
const int maxn = 3e3+10;
int n,m,s,t;
vector<int> g[maxn];
struct ss{
 	int v,w,nxt;
}edg[500*maxn];
int head[maxn],cnt,deep[maxn],cur[maxn];
void init(){
 	cnt = 0;
 	memset(head,-1,sizeof(head));
}
void add(int x,int y,int w){
 	edg[cnt].v=y;
 	edg[cnt].nxt=head[x];
 	edg[cnt].w=w;
 	head[x]=cnt++;
}
bool bfs(int s,int t){
 	memset(deep,0,sizeof(deep));
 	queue<int> pq;
 	pq.push(s);
 	deep[s]=1;
 	while(!pq.empty()){
 		int top=pq.front();
  		pq.pop();
  		for(int i = head[top]; i + 1; i = edg[i].nxt){
   			int v=edg[i].v;
   			int w=edg[i].w;
   			if(w>0&&!deep[v]){
    				deep[v]=deep[top]+1;
    				pq.push(v);
   			}
  		}
 	}
 	return deep[t]!=0;
}
int dfs(int s,int t,int flow){
 	if(s==t) return flow;
 	int res=0;
 	for(int &i = cur[s]; i+1 ; i=edg[i].nxt){
 		int v=edg[i].v;
  		int &w=edg[i].w;
  		int x = 0;
  		if(deep[v]==deep[s]+1&&w>0){
   			x=dfs(v,t,min(flow,w));
   			w-=x;flow-=x;res+=x;edg[i^1].w+=x;
   			if(!flow) break;
  		}
 	}
 	if(!res) deep[s]=-2;
 	return res;
}
int dinic(int s,int t){
 	int res=0;
 	while(bfs(s,t)){
  		for(int i = 1; i <= maxn; i++) 
   			cur[i]=head[i];
  		res+=dfs(s,t,0x3f3f3f3f);
 	}	
 	return res;
}
int main(){
 	scanf("%d%d%d%d",&n,&m,&s,&t);
 	int x,y;
 	init();
 	for(int i = 1; i <= m; i++){
  		scanf("%d%d",&x,&y);
  		g[x].push_back(y);
  		g[y].push_back(x);
 	}
 	for(int i = 1; i <= n; i++){
  		add(i,i+n,1);
  		add(i+n,i,0);
  		for(int j = 0; j < g[i].size(); j++){
   			add(i+n,g[i][j],0x3f3f3f3f);
   			add(g[i][j],i+n,0);
  		}
 	}	
	printf("%d\n",dinic(s+n,t));
}