introduction:

Sorting algorithm is one of the most basic algorithms in data structure and algorithm. Here are ten classic sorting algorithms to explain. Taoist friends who don't know can come here to sweep away their blindness. From "rookie tutorial".

explain

   sorting algorithms can be divided into internal sorting and external sorting. Internal sorting is to sort data records in memory, while external sorting is to access external memory in the sorting process because the sorted data is large and can not accommodate all sorting records at one time. Common internal sorting algorithms include: insert sort, Hill sort, select sort, bubble sort, merge sort, quick sort, heap sort, cardinal sort, etc. Summarize with the following figure:

"Risk, select, insert and return to fast reactor, count, base, barrel"

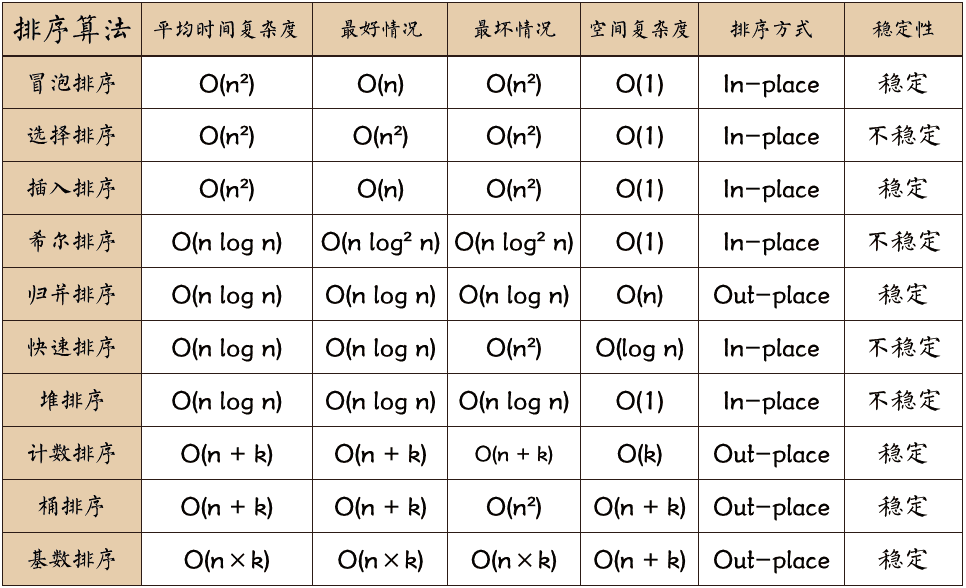
Explanation of terms:

• n: Data scale
• k: Number of "barrels"
• In place: occupy constant memory and no additional memory
• Out place: use extra memory
• Stability: the order of the two equal key values after sorting is the same as that before sorting

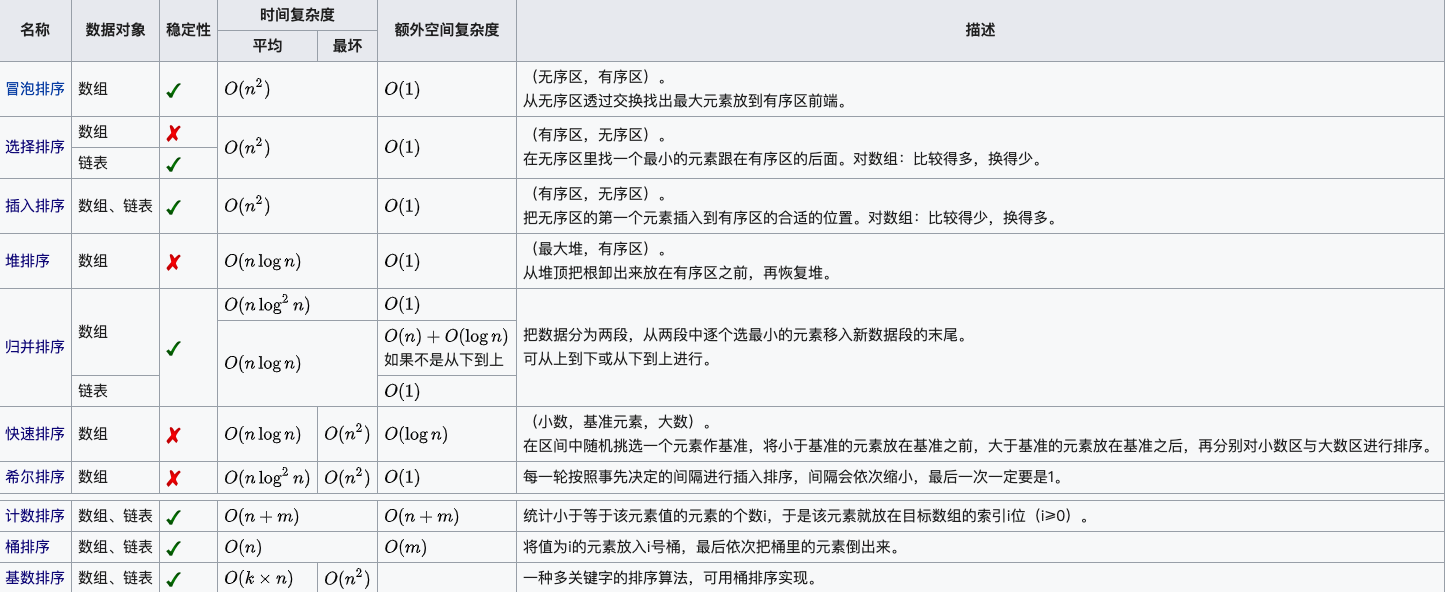
• Square order O(n2) sorting various simple sorting: direct insertion, direct selection and bubble sorting.
• Linear logarithmic order (O(nlog2n)) sort: quick sort, heap sort and return side by side.
  O(n1 + §) sort, § is a constant between 0 and 1: Hill sort.
• Linear order O(n) sorting: Radix sorting, in addition to bucket and box sorting.
• Stable sorting algorithms: bubble sort, insert sort, merge sort and cardinal sort.
• Unstable sorting algorithms: selective sorting, quick sorting, Hill sorting and heap sorting.

1, Bubble sorting

Bubble Sort is also a simple and intuitive sorting algorithm. It repeatedly visits the sequence to be sorted, compares two elements at a time, and exchanges them if they are in the wrong order. The work of visiting the sequence is repeated until there is no need to exchange, that is, the sequence has been sorted. The name of this algorithm comes from the fact that smaller elements will slowly "float" to the top of the sequence through exchange.
   as one of the simplest sorting algorithms, bubble sorting gives me the same feeling as Abandon appears in the word book. It is the first place on the first page every time, so I am most familiar with it. Another optimization algorithm for bubble sorting is to set up a flag. When there is no exchange of elements in a sequence traversal, it proves that the sequence has been ordered. However, this improvement has little effect on improving performance.

1. Algorithm steps

• Compare adjacent elements. If the first one is bigger than the second, exchange them.
• Do the same for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end. After this step, the last element will be the maximum number.
• Repeat the above steps for all elements except the last one.
• Continue to repeat the above steps for fewer and fewer elements at a time until no pair of numbers need to be compared.

2. Animation demonstration

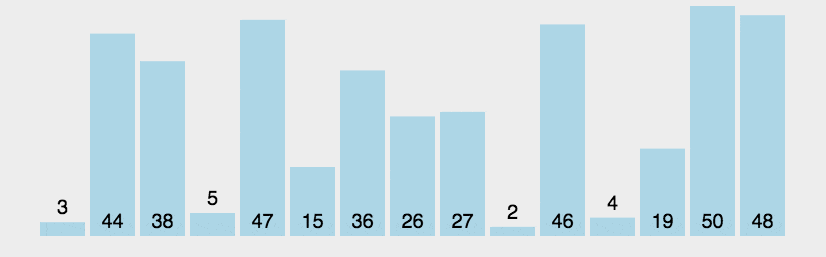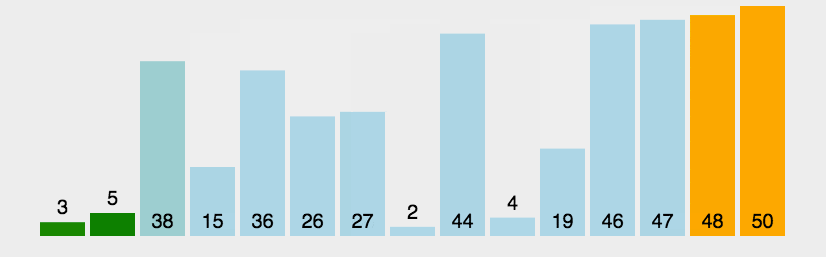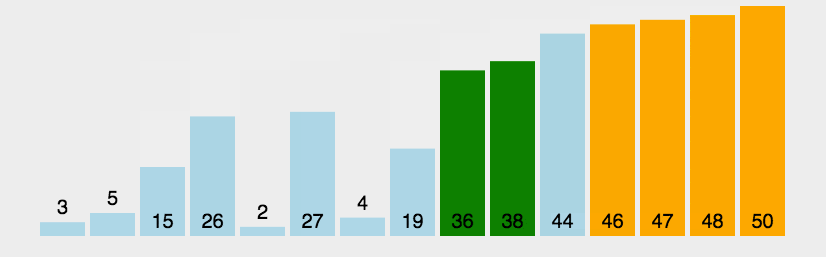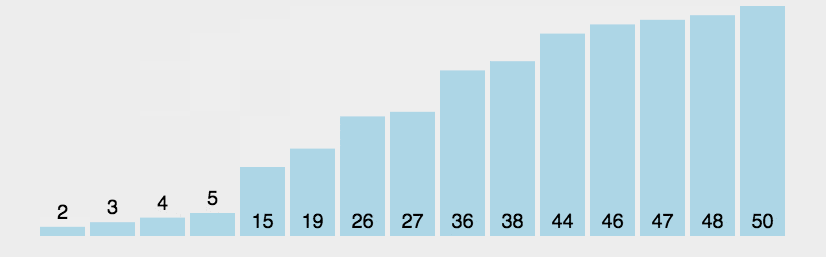
3. java code example

public int[] bubbleSort(int[] sourceArray) {
    int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

    for (int i = 1; i < arr.length; i++) {
        boolean flag = true;//Mark. If true, it indicates that there is no exchange in this cycle
        for (int j = 0; j < arr.length - i; j++) {
            if (arr[j] > arr[j + 1]) {
                int tmp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = tmp;
                flag = false;
            }
        }
        if (flag) break;
    }
    return arr;
}

2, Select sort

   selective sorting is a simple and intuitive sorting algorithm. No matter what data goes in, it is the time complexity of O(n2). So when using it, the smaller the data scale, the better. The only advantage may be that it doesn't take up extra memory space.

1. Algorithm steps

• First, find the smallest (large) element in the unordered sequence and store it at the beginning of the sorted sequence.
• Then continue to find the smallest (large) element from the remaining unordered elements, and then put it at the end of the sorted sequence.
• Repeat step 2 until all elements are sorted.

2. Animation demonstration

3. java code example

public int[] selectionSort(int[] sourceArray) {
	int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

    // A total of N-1 rounds of comparison are required
    for (int i = 0; i < arr.length - 1; i++) {
        int min = i;

        // Number of comparisons per round N-i
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[j] < arr[min]) {
                min = j; // Record the subscript of the lowest value element that can be found at present
            }
        }

        // Exchange the minimum value found with the value of i position
        if (i != min) {
            int tmp = arr[i];
            arr[i] = arr[min];
            arr[min] = tmp;
        }
    }
    return arr;
}

3, Insert sort

   the code implementation of insertion sorting is not as simple and crude as bubble sorting and selection sorting, but its principle should be the easiest to understand. Insert sort is the simplest and most intuitive sort algorithm. Its working principle is to build an ordered sequence, scan the unordered data from back to front in the sorted sequence, find the corresponding position and insert. Like bubble sort, insertion sort also has an optimization algorithm called split half insertion.

1. Algorithm steps

• The first element of the sort sequence is regarded as an ordered sequence, and the second element to the last element is regarded as an unordered sequence.
• Scan the unordered sequence from beginning to end, and insert each scanned element into the appropriate position of the ordered sequence. (if the element to be inserted is equal to an element in the ordered sequence, insert the element to be inserted after the equal element to maintain stability)

2. Animation demonstration

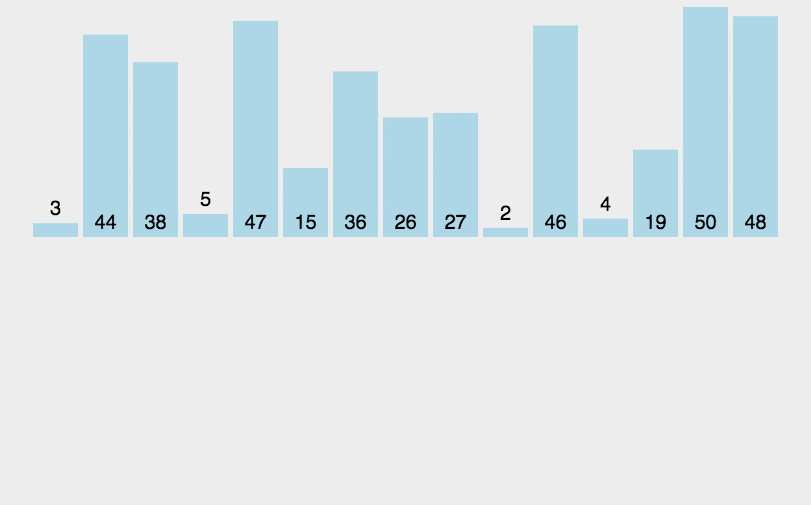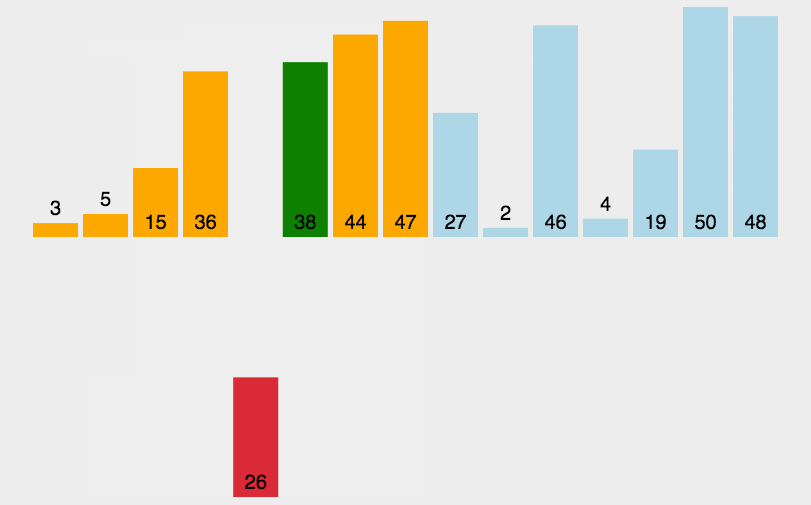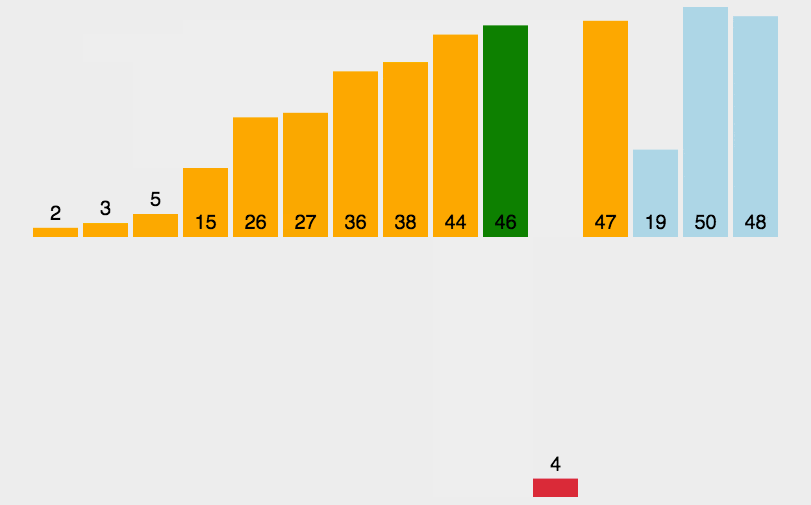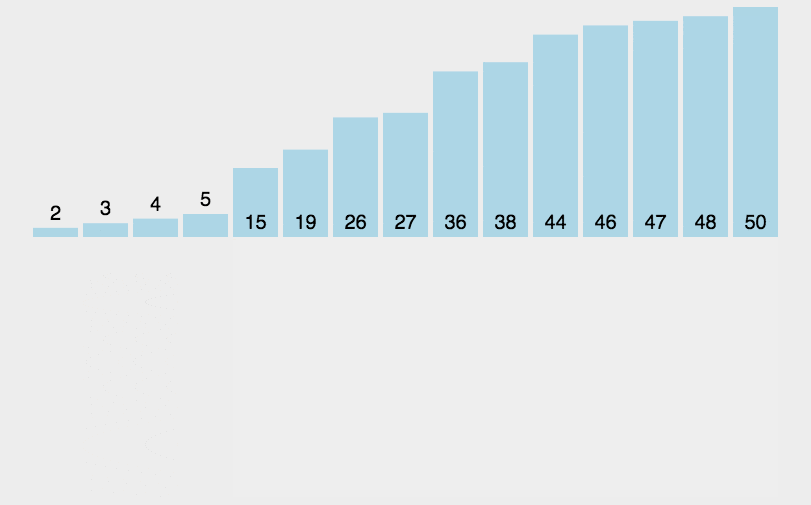
3. java code example

public int[] insertSort(int[] sourceArray) {
	int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

    // Select the appropriate position to insert from the element with subscript 1, because there is only one element with subscript 0, which is ordered by default
    for (int i = 1; i < arr.length; i++) {
        int tmp = arr[i]; // Record the data to be inserted

        // Compare from the rightmost of the sorted sequence to find a smaller number
        int j = i;
        while (j > 0 && tmp < arr[j - 1]) {
            arr[j] = arr[j - 1]; // Move the j-1 element back
            j--;
        }

        // There is a smaller number than it, insert
        if (j != i) arr[j] = tmp;
    }
    return arr;
}

4, Hill sort

Hill sort, also known as decreasing incremental sort algorithm, is a more efficient improved version of insertion sort. But Hill sorting is an unstable sorting algorithm. Hill sort is an improved method based on the following two properties of insertion sort:

• Insertion sorting is efficient when operating on almost ordered data, that is, it can achieve the efficiency of linear sorting;
• However, insertion sorting is generally inefficient, because insertion sorting can only move data one bit at a time;

The basic idea of Hill sort is: first divide the whole record sequence to be sorted into several subsequences for direct insertion sort. When the records in the whole sequence are "basically orderly", then directly insert sort all records in turn.

1. Algorithm steps

• Select an incremental sequence t1, t2,..., tk, where ti > TJ, tk = 1;
• Sort the sequence k times according to the number of incremental sequences k;
• For each sorting, the sequence to be sorted is divided into several subsequences with length m according to the corresponding increment ti, and each sub table is directly inserted and sorted. Only when the increment factor is 1, the whole sequence is treated as a table, and the table length is the length of the whole sequence.

2. Animation demonstration

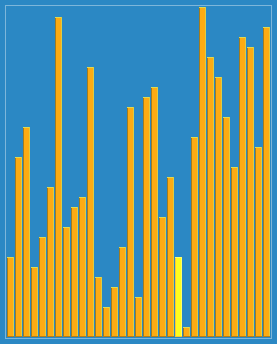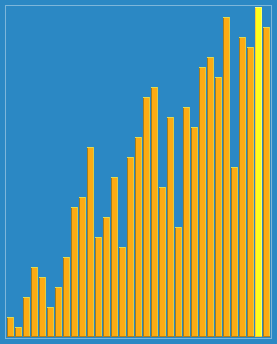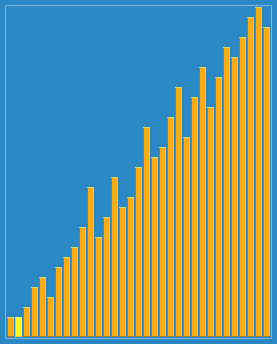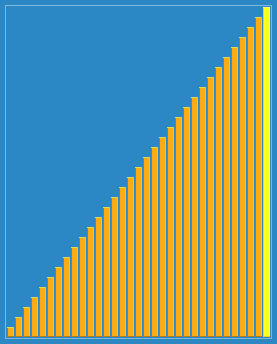
3. java code example

public void shellSort(int[] arr){
	int length = arr.length;
    int temp;
    for (int step = length / 2; step >= 1; step /= 2) {//step is equivalent to increment
        for (int i = step; i < length; i++) {
            temp = arr[i];
            int j = i - step;
            while (j >= 0 && arr[j] > temp) {
                arr[j + step] = arr[j];
                j -= step;
            }
            arr[j + step] = temp;
        }
    }
}

5, Merge sort

Merge sort is an effective sort algorithm based on merge operation. The algorithm is a very typical application of Divide and Conquer. As a typical algorithmic application of the idea of Divide and Conquer, the implementation of merge sorting consists of two methods:

• Top down recursion (all recursive methods can be rewritten iteratively, so there is the second method)
• Bottom up recursion

   like selective sorting, the performance of merge sorting is not affected by the input data, but it performs much better than selective sorting, because it is always O(nlogn) time complexity. The cost is the need for additional memory space.

1. Algorithm steps

• Apply for space so that its size is the sum of two sorted sequences, and the space is used to store the merged sequences;
• Set two pointers, and the initial position is the starting position of the two sorted sequences respectively;
• Compare the elements pointed to by the two pointers, select the relatively small element and put it into the merge space, and move the pointer to the next position;
• Repeat step 3 until a pointer reaches the end of the sequence;
• Copy all the remaining elements of another sequence directly to the end of the merged sequence.

2. Animation demonstration

3. java code example

public class MergeSort {
    public int[] sort(int[] sourceArray) throws Exception {
        // Copy the arr without changing the parameters
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

        if (arr.length < 2) return arr;// What else is this row

        int middle = (int) Math.floor(arr.length / 2);
        int[] left = Arrays.copyOfRange(arr, 0, middle);
        int[] right = Arrays.copyOfRange(arr, middle, arr.length);

        return merge(sort(left), sort(right));
    }

    protected int[] merge(int[] left, int[] right) {
        int[] result = new int[left.length + right.length];
        int i = 0;
        while (left.length > 0 && right.length > 0) {
            if (left[0] <= right[0]) {
                result[i++] = left[0];
                left = Arrays.copyOfRange(left, 1, left.length);
            } else {
                result[i++] = right[0];
                right = Arrays.copyOfRange(right, 1, right.length);
            }
        }

        while (left.length > 0) {
            result[i++] = left[0];
            left = Arrays.copyOfRange(left, 1, left.length);
        }

        while (right.length > 0) {
            result[i++] = right[0];
            right = Arrays.copyOfRange(right, 1, right.length);
        }

        return result;
    }
}

6, Quick sort

  on average, n items should be sorted Ο (nlogn) comparisons. In the worst case, you need Ο (n2) times, but this situation is not common. In fact, quick sort is usually significantly better than others Ο (nlogn) algorithm is faster because its inner loop can be implemented efficiently on most architectures.
  quick sort uses Divide and conquer strategy to divide a list into two sub lists. Quick sorting is a typical application of Divide and conquer in sorting algorithm. In essence, quick sort should be a recursive Divide and conquer method based on bubble sort. The name of quick sort is simple and rough, because as soon as you hear the name, you know the meaning of its existence, which is fast and efficient! It is one of the fastest sorting algorithms to process big data. Although the time complexity of Worst Case reaches O(n ²)， But others are excellent. In most cases, they perform better than the sorting algorithm with an average time complexity of O(n logn), but I don't know why.

Algorithmic art and informatics competition: the worst case of quick sorting is O(n ²)， For example, the fast arrangement of sequential sequence. However, the expected spreading time is O(nlogn), and the constant factor implicit in the O(nlogn) sign is very small, which is much smaller than the merging sort with stable complexity equal to O(nlogn). Therefore, for the vast majority of random sequences with weak order, quick sorting is always better than merge sorting.

1. Algorithm steps

• Pick out an element from the sequence, called "pivot", and usually select the first element;
• Reorder the sequence. All elements smaller than the benchmark value are placed in front of the benchmark, and all elements larger than the benchmark value are placed behind the benchmark (the same number can be on either side). After the partition exits, the benchmark is in the middle of the sequence. This is called a partition operation;
• Recursively sort the subsequence less than the reference value element and the subsequence greater than the reference value element;

2. Animation demonstration

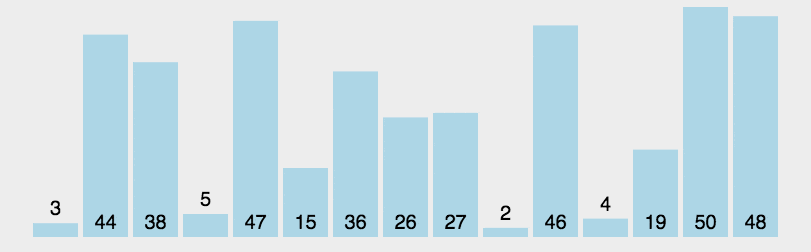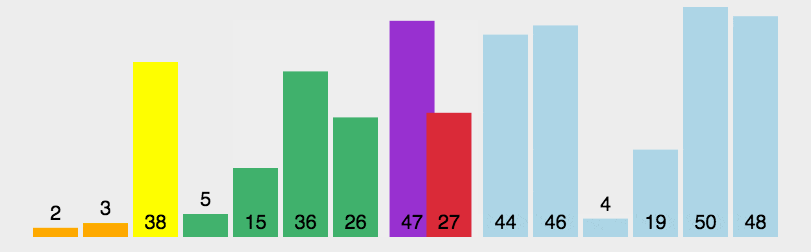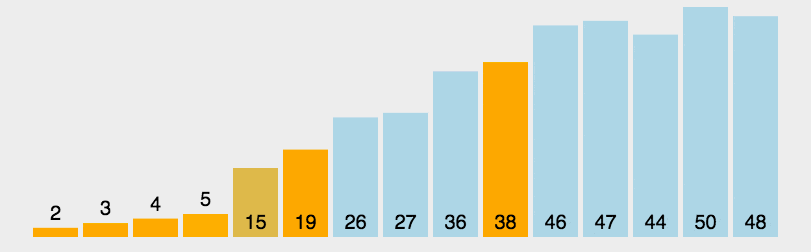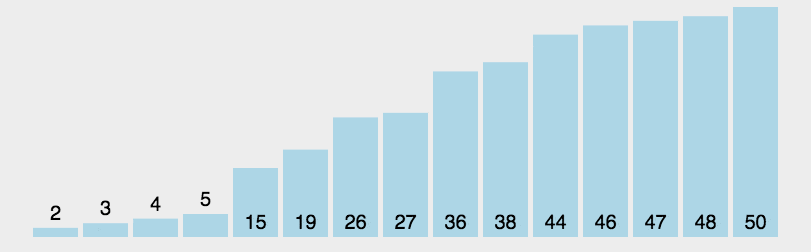
3. java code example 1 (left and right pit filling each other)

//Quick sort. Left and right pit excavation and mutual filling
void quickSort(int[] s, int l, int r) {
    if (l < r) {
        int i = l, j = r;
        int x = s[l]; //The first digit benchmark is selected by default, and other numbers can also be exchanged to the position of the first number as the benchmark
        while (i < j) {
            while (s[j] >= x && i < j) j--; // Find the first number less than x from right to left
            if (i < j) s[i++] = s[j];
            while (s[i] < x && i < j) i++;  // Find the first number greater than or equal to x from left to right
            if(i<j) s[j--] = s[i];
        }
        s[i] = x;
        quickSort(s, l, i - 1); //Recursive call
        quickSort(s, i + 1, r);
    }
}

4. java code example 2 (left-right exchange)

//Quick sort. Left right exchange
void quickSort(int[] s, int l, int r) {
    if (l < r) {
        int i = l, j = r;
        int temp = s[i];
        while (i < j) {
            while (s[j] >= s[l] && i < j) j--;
            while (s[i] <= s[l] && i < j) i++;
            temp = s[i]; //Exchange i and j position elements
            s[i] = s[j];
            s[j] = temp;
        }
        s[i] = s[l]; //Exchange i and l position elements
        s[l] = temp;
        quickSort(s, l, i - 1); //Recursive call
        quickSort(s, i + 1, r);
    }
}

5. java code example 3 (auxiliary function)

public class QuickSort {
    public int[] sort(int[] sourceArray) throws Exception {
        // Do not change the parameters of arr
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
        return quickSort(arr, 0, arr.length - 1);
    }

    private int[] quickSort(int[] arr, int left, int right) {
        if (left < right) {
            int partitionIndex = partition(arr, left, right);
            quickSort(arr, left, partitionIndex - 1);
            quickSort(arr, partitionIndex + 1, right);
        }
        return arr;
    }

    private int partition(int[] arr, int left, int right) {
        int pivot = left;// Set reference value (pivot)
        int index = pivot + 1;
        for (int i = index; i <= right; i++) {
            if (arr[i] < arr[pivot]) {
                swap(arr, i, index);
                index++;
            }
        }
        swap(arr, pivot, index - 1);
        return index - 1;
    }

    private void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

7, Heap sort

Heap sort refers to a sort algorithm designed by using the data structure of heap. Heap is a structure similar to a complete binary tree, and satisfies the nature of heap at the same time: that is, the key value or index of a child node is always less than (or greater than) its parent node. Heap sort can be said to be a selective sort that uses the concept of heap to sort. There are two methods:

• Large top heap: the value of each node is greater than or equal to the value of its child nodes, which is used for ascending arrangement in heap sorting algorithm;
• Small top heap: the value of each node is less than or equal to the value of its child nodes, which is used for descending arrangement in heap sorting algorithm;

The average time complexity of heap sorting is Ο (nlogn).

1. Algorithm steps

• Create a heap H[0... n-1];
• Swap the head (maximum) and tail of the reactor;
• Reduce the size of the heap by 1 and call shift_down(0), the purpose is to adjust the data at the top of the new array to the corresponding position (which can be understood as heap);
• Repeat step 2 until the heap size is 1.

2. Animation demonstration

3. java code example 1 (recursive heap)

public class HeapSort {
    public int[] sort(int[] sourceArray) throws Exception {
        // Copy the arr without changing the parameters
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

        int len = arr.length;
        buildMaxHeap(arr, len);

        for (int i = len - 1; i > 0; i--) {
            swap(arr, 0, i);
            len--;
            heapify(arr, 0, len);
        }
        return arr;
    }

	//Bottom up stacking
    private void buildMaxHeap(int[] arr, int len) {
        for (int i = (int) Math.floor(len / 2); i >= 0; i--) {
            heapify(arr, i, len);
        }
    }

	//In fact, the properties of the parent node mentioned above are guaranteed to be satisfied
    private void heapify(int[] arr, int i, int len) {
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int largest = i;

        if (left < len && arr[left] > arr[largest]) largest = left;
        if (right < len && arr[right] > arr[largest]) largest = right;

        if (largest != i) {
            swap(arr, i, largest);
            heapify(arr, largest, len);
        }
    }

    private void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

java code example 2 (iterative heap)

public int[] heapSort(int[] sourceArray) {
    // Copy the arr without changing the parameters
    int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

    //Pile up from bottom to top
    for (int i = 1; i < arr.length; i++) {
        int child = i;
        int root = (child - 1) / 2;//Parent node
        while (arr[child] > arr[root]) {
            swap(arr, child, root);
            child = root;
            root = (child - 1) / 2;
        }
    }
    //The first element is exchanged backward and stacked from top to bottom
    for (int i = arr.length - 1; i > 0; i--) {
        swap(arr, 0, i);
        int root = 0;
        while (true) {
            int left = root * 2 + 1, right = root * 2 + 2;//Left and right children in principle
            int maxChild = root;
            if (left < i && arr[left] > arr[maxChild]) maxChild = left;
            if (right < i && arr[right] > arr[maxChild]) maxChild = right;
            if (maxChild != root) {
                swap(arr, root, maxChild);
                root = maxChild;
            } else break;
        }
    }
    return arr;
}

private void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

8, Count sort

   the core of counting and sorting is to convert the input data values into keys and store them in the additional array space. As a sort with linear time complexity, count sort requires that the input data must be integers with a certain range** Features: * * when the input element is n integers between 0 and K, its running time is Θ (n + k). Counting sorting is not a comparative sorting, and the sorting speed is faster than any comparative sorting algorithm.
   since the length of array C used for counting depends on the range of data in the array to be sorted (equal to the difference between the maximum and minimum values of the array to be sorted plus 1), counting sorting requires a lot of time and memory for arrays with large data range. For example, counting sorting is the best algorithm for sorting numbers between 0 and 100, but it is not suitable for sorting names alphabetically. However, counting sorting can be used in the algorithm of cardinality sorting to sort arrays with a large range of data.
   generally speaking, for example, there are 10 people of different ages. According to the statistics, 8 people are younger than A, and A's age ranks ninth. Using this method, we can get the position of everyone else, which is in good order. Of course, special treatment is required when there are repetitions of age (to ensure stability), which is why the target array should be backfilled and the statistics of each number should be subtracted by 1.

1. Algorithm steps

• Find the largest and smallest elements in the array to be sorted
• Count the number of occurrences of each element with value i in the array and store it in the ith item of array C
• All counts are accumulated (starting from the first element in C, and each item is added to the previous item)
• Reverse fill the target array: put each element i in item C(i) of the new array, and subtract 1 from C(i) for each element

2. Animation demonstration

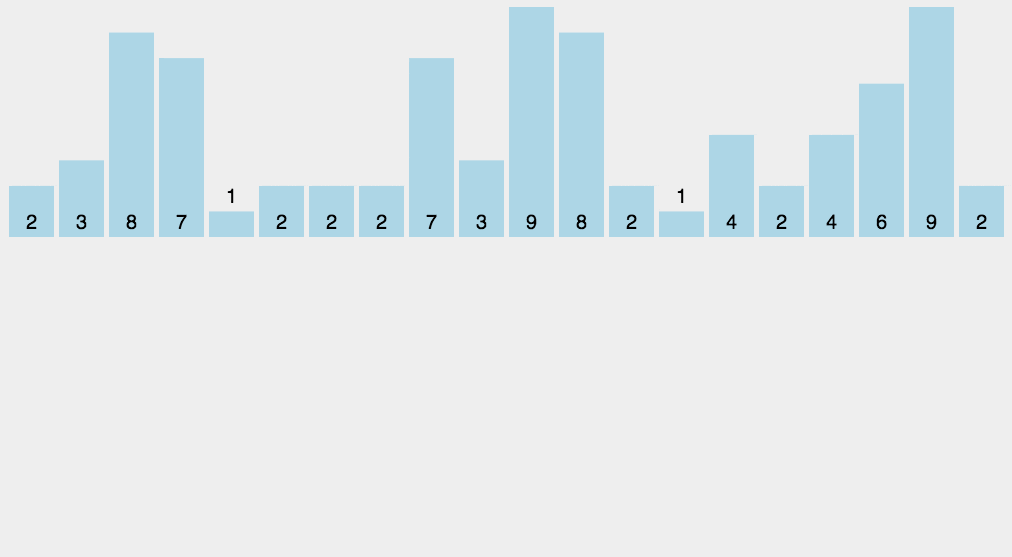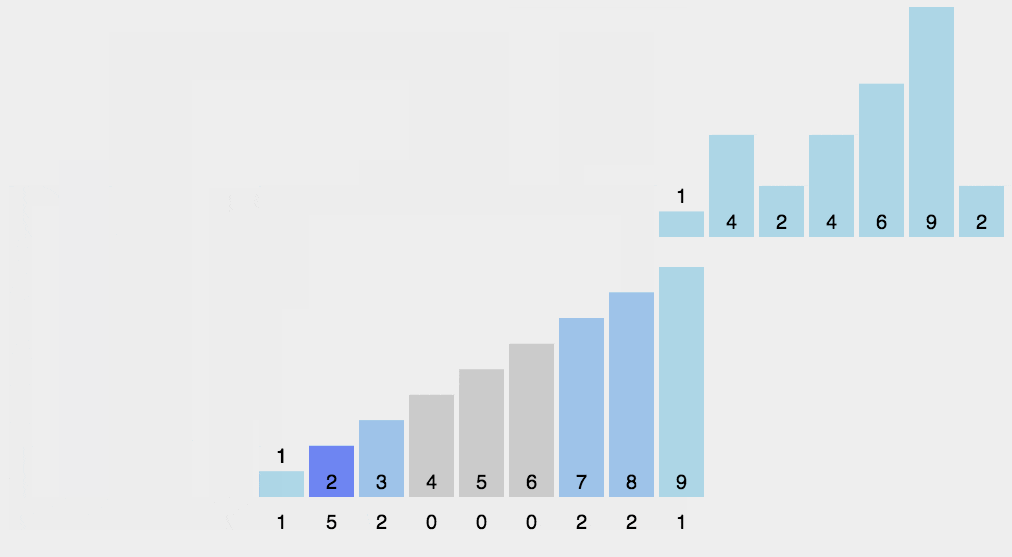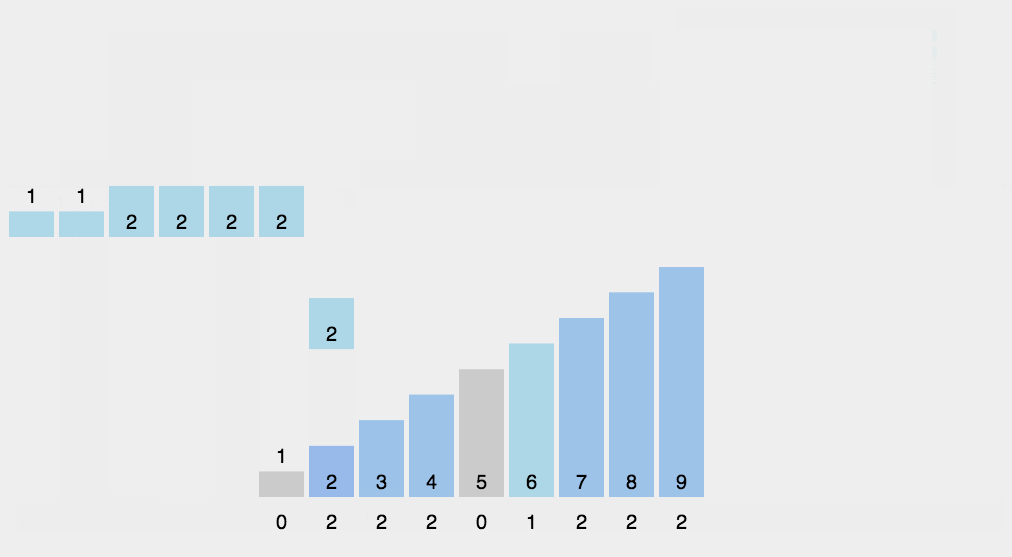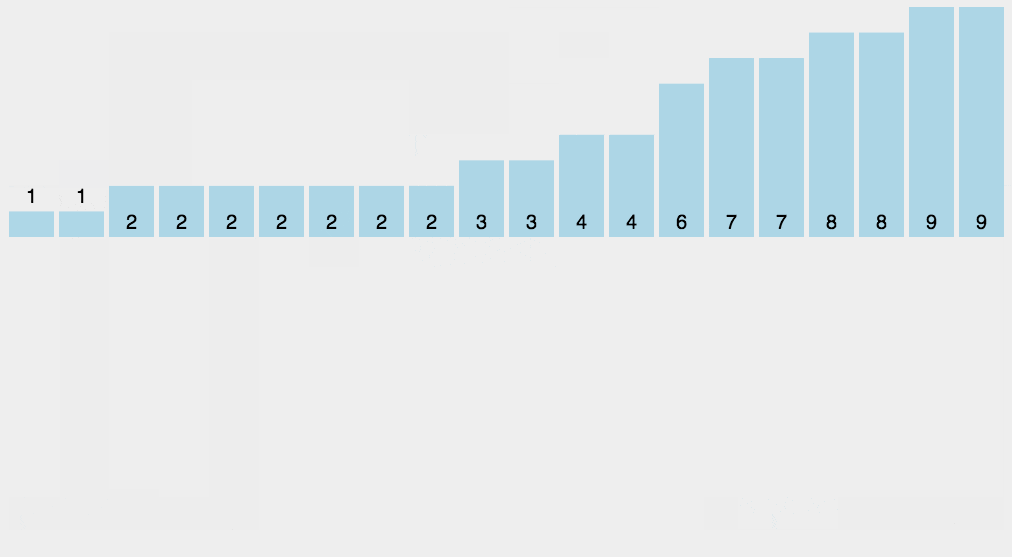
3. java code example

public int[] countingSort(int[]  sourceArray){
    // Do not change the parameters of arr
    int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

    // Find the maximum and minimum value
    int min = arr[0], max = arr[0];
    for (int num : arr) {
        if (num < min) min = num;
        if (num > max) max = num;
    }

    // count
    int[] count = new int[max - min + 1];
    for (int num : arr) count[num - min]++;

    int sortedIndex = 0;
    for (int i = 0; i < count.length; i++) {
        while (count[i]-- > 0) {
            arr[sortedIndex++] = min + i;
        }
    }
    return arr;
}

9, Bucket sorting

Bucket sorting is an upgraded version of counting sorting. It makes use of the mapping relationship of the function. The key to efficiency lies in the determination of the mapping function. In order to make bucket sorting more efficient, we need to do these two things:

• When there is enough extra space, try to increase the number of barrels
• The mapping function used can evenly distribute the input N data into K buckets

  at the same time, for the sorting of elements in the bucket, it is very important to choose a comparison sorting algorithm for performance** When is the fastest: * * when the input data can be evenly distributed into each bucket** When is the slowest: * * when the input data is allocated to the same bucket.

1. Animation demonstration

Elements are distributed in the bucket	Elements are sorted in each bucket

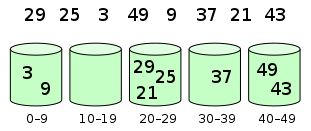2. java code example

public int[] bucketSort(int[]  sourceArray, int bucketSize){
    // Do not change the parameters of arr
    int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

    // Find the maximum and minimum value
    int min = arr[0], max = arr[0];
    for (int num : arr) {
        if (num < min) min = num;
        if (num > max) max = num;
    }

    int bucketCount = (int) Math.floor((max - min) / bucketSize) + 1;
    int[][] buckets = new int[bucketCount][0];

    // The mapping function is used to allocate the data to each bucket
    for (int i = 0; i < arr.length; i++) {
        int index = (int) Math.floor((arr[i] - min) / bucketSize);
        buckets[index] = arrAppend(buckets[index], arr[i]);
    }

    int arrIndex = 0;
    for (int[] bucket : buckets) {
        if (bucket.length <= 0) continue;
        bucket = insertSort(bucket);// Sort each bucket. Insert sort is used here
        for (int value : bucket) {
            arr[arrIndex++] = value;
        }
    }

    return arr;
}

// Automatically expand capacity and save data
private int[] arrAppend(int[] arr, int value){
    arr = Arrays.copyOf(arr, arr.length + 1);
    arr[arr.length - 1] = value;
    return arr;
}

// Insert sort
private int[] insertSort(int[] sourceArray){
    int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
    for (int i = 1; i < arr.length; i++) {
        int temp = arr[i]; //Record the data to be inserted
        // Compare from the rightmost side of the sorted sequence to find a smaller number
        int j = i;
        while (j > 0 && arr[j - 1] > temp) {
            arr[j] = arr[j - 1];
            j--;
        }
        if (j != i) arr[j] = temp;
    }
    return arr;
}

10, Cardinality sort

   Radix sorting is a non comparative integer sorting algorithm. Its principle is to cut integers into different numbers according to the number of digits, and then compare them respectively according to each number of digits. Since integers can also express strings (such as names or dates) and floating-point numbers in a specific format, cardinality sorting is not limited to integers.
**Cardinality sorting vs counting sorting vs bucket sorting: * * these three sorting algorithms all use the concept of bucket, but there are obvious differences in the use of bucket:

• Cardinality sorting: allocate buckets according to each number of key value;
• Counting and sorting: only one key value is stored in each bucket;
• Bucket sorting: each bucket stores a certain range of values;

There are two methods of cardinality sorting:
   most significant digital first method (MSD method for short): first sort and group the records according to k1, and the key codes k1 are equal in the same group, then sort each group according to k2 and divide them into subgroups, and then continue to sort and group the following key codes until the subgroups are sorted according to the lowest key code kd. Then connect the groups to get an ordered sequence.
   least significant digital first method (LSD method for short): first sort from kd, then sort kd-1, repeat in turn, and get an ordered sequence after sorting k1.
   the cardinality sorting of LSD is applicable to the sequence with small digits. If there are many digits, the efficiency of using MSD will be better. In contrast to LSD, MSD is allocated from the high-order number as the base, but it is not merged back into an array immediately after allocation. Instead, a "sub bucket" is established in each "bucket", and the value in each bucket is allocated to the "sub bucket" according to the value of the next digit. After the allocation of the lowest digits is completed, it will be merged into the array of receipt 1.

1. Animation demonstration

2. java code example

public class RadixSort {
    public int[] sort(int[] sourceArray) {
        // Do not change the parameters of arr
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

        int maxDigit = getMaxDigit(arr);
        return radixSort(arr, maxDigit);
    }

    // Get the highest number of digits
    private int getMaxDigit(int[] arr) {
        int maxValue = getMaxValue(arr);
        return getNumLenght(maxValue);
    }

    private int getMaxValue(int[] arr) {
        int maxValue = arr[0];
        for (int value : arr) {
            if (maxValue < value) maxValue = value;
        }
        return maxValue;
    }

    protected int getNumLenght(long num) {
        if (num == 0) return 1;
        int lenght = 0;
        for (long temp = num; temp != 0; temp /= 10) {
            lenght++;
        }
        return lenght;
    }

    private int[] radixSort(int[] arr, int maxDigit) {
        int mod = 10;
        int dev = 1;

        for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
            // Considering the negative number, the number of queues is doubled here, where [0-9] corresponds to a negative number and [10-19] corresponds to a positive number (bucket + 10)
            int[][] counter = new int[mod * 2][0];

            for (int j = 0; j < arr.length; j++) {
                int bucket = ((arr[j] % mod) / dev) + mod;
                counter[bucket] = arrayAppend(counter[bucket], arr[j]);
            }

            int pos = 0;
            for (int[] bucket : counter) {
                for (int value : bucket) {
                    arr[pos++] = value;
                }
            }
        }

        return arr;
    }

    // Automatically expand capacity and save data
    private int[] arrayAppend(int[] arr, int value) {
        arr = Arrays.copyOf(arr, arr.length + 1);
        arr[arr.length - 1] = value;
        return arr;
    }
}