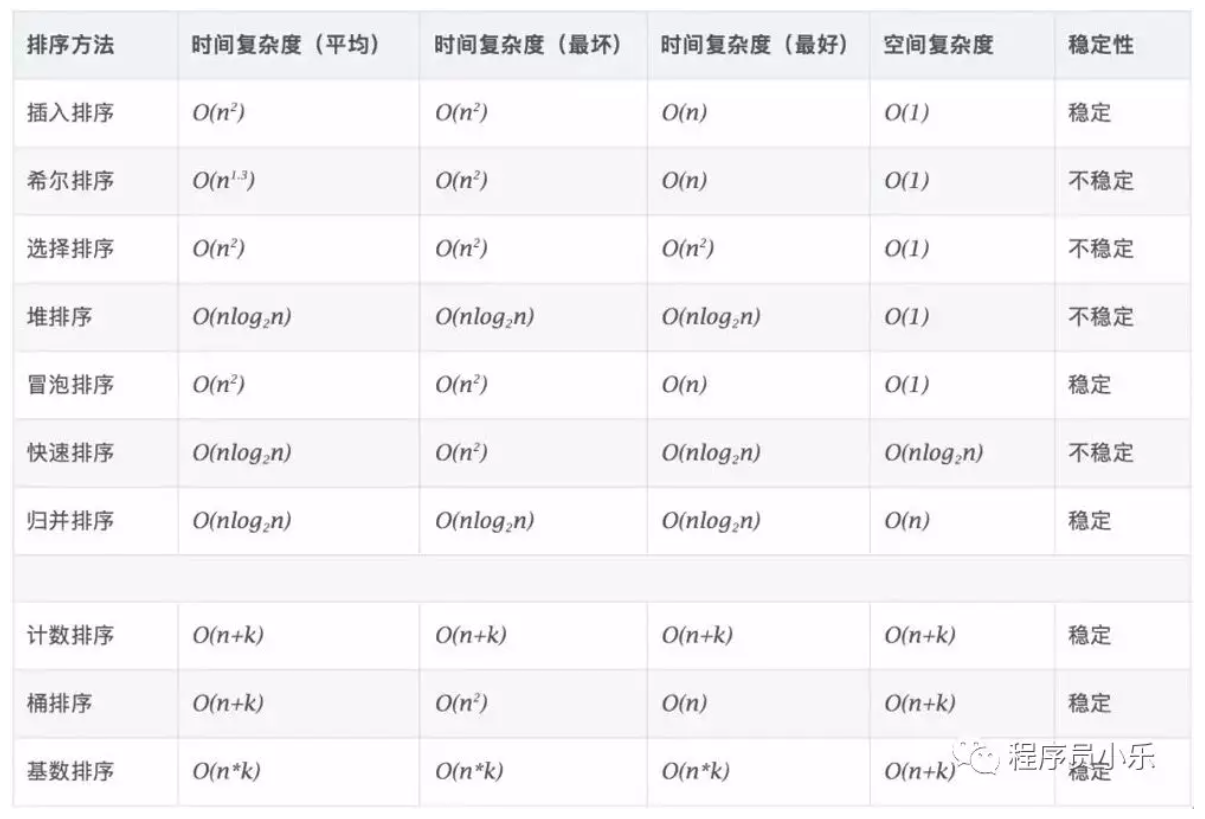
Top ten sorting algorithms
Properties of sorting algorithm
OI Wiki: introduction to sorting
- Stability: whether the relative order * * of equal elements has changed after sorting.
- Time complexity: time complexity is divided into optimal time complexity, average time complexity and worst time complexity.
Select sort
Algorithm idea
The algorithm idea of selecting sorting is to find out the smallest (or largest) element of the remaining elements each time and put it in the front position in order (the specific operation is to exchange with the front elements).
stability
Due to the existence of swap (exchange two elements) operation, selective sorting is an unstable sorting algorithm.
For example, when the array [6, 7, 6, 2, 8] is cycled for the first time, the 6 in the first position will be exchanged with the following 2. At this time, the relative front and rear positions of the two 6 have been changed.
Time complexity
The optimal time complexity, average time complexity and worst time complexity of the selected sorting are O(n^2).
code implementation
// Java Version
public void selectionSort(int[] arr) {
int len = arr.length;
for (int i = 0; i < len - 1; i++) {
int idx = i;
// Find the smallest of the remaining elements
for (int j = i + 1; j < len; j++) {
if (arr[j] < arr[idx]) {
idx = j;
}
}
// Exchange element
int temp = arr[i];
arr[i] = arr[idx];
arr[idx] = temp;
}
}
Bubble sorting
Algorithm idea
The algorithm idea of bubble sorting is to check two adjacent elements each time. If the front element and the rear element meet the given sorting conditions, the two adjacent elements will be exchanged. When no adjacent elements need to be exchanged, the sorting is completed.
After i scans, the i item at the end of the sequence must be the largest i item, so bubble sorting can be completed by scanning the array n - 1 times at most.
stability
Bubble sorting is a stable sorting algorithm.
Time complexity
- The best case: when the sequence is completely ordered, bubble sorting only needs to traverse the array once without performing any exchange operation, and the time complexity is O(n).
- In the worst case, bubble sorting needs to perform n * (n - 1) / 2 exchange operations, and the time complexity is O(n^2).
- The average time complexity of bubble sorting is O(n^2).
code implementation
// Java Version
public void bubbleSort(int[] arr) {
int len = arr.length;
boolean flag = true;
while (flag) {
flag = false;
for (int i = 0; i < len - 1; i++) {
if (arr[i] > arr[i + 1]) {
flag = true;
int temp = arr[i];
arr[i] = arr[i + 1];
arr[i + 1] = temp;
}
}
}
}
Insert sort
Algorithm idea
The algorithm idea of insertion sorting is to divide the elements to be arranged into "sorted" and "unordered", and select one of the "unordered" elements to insert into the correct position in the "sorted" element each time.
stability
Insertion sort is a stable sort algorithm.
Time complexity
The optimal time complexity of insertion sorting is O(n), which is very efficient when the sequence is almost ordered.
The worst time complexity and average time complexity of insertion sort are O(n^2).
Algorithm implementation
// Java Version
public void InsertionSort(int[] arr) {
int len = arr.length;
for (int i = 1; i < len; i++) {
int now = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > now) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = now;
}
}
Shell Sort
Little gray cartoon: what is Hill sort
Algorithm idea
Hill sort (English: Shell sort), also known as reduced incremental sorting, is Insert sort An improved version of. Hill sort is named after its inventor, Donald Shell.
Sorting compares and moves non adjacent records:
- The sequence to be sorted is divided into several subsequences (the elements of each subsequence are the same in the middle distance of the original array);
- Insert sorting in subsequence;
- Reduce the spacing between elements in each subsequence and repeat the above process until the spacing is reduced to 1.
The group spacing, known as the increment of Hill sort, is a simple method proposed by Donald Shell when inventing Hill sort, which is called Hill increment.
stability
Hill sorting is an unstable sorting algorithm.
Time complexity
The optimal time complexity of hill sorting is O(n).
The average time complexity and worst-case time complexity of hill sorting are related to the selection of spacing sequence (that is, how to reduce the spacing to 1). For example, the time complexity of hill sorting with "spacing divided by k every time" is O(n^(k/2)). It is known that the best and worst time complexity is O(n(logn)^2).
code implementation
// Java Version
/**
* Shell Increment: 1, 2, 4 len / 2
* General term formula: 2^k
* The worst time complexity is still O(n^2), sometimes even slower than using insert sorting directly.
* The reason is that each round of hill sorting is proportional, resulting in a blind area in hill increment.
* @param arr Array to be sorted
*/
public void shellSort(int[] arr) {
int len = arr.length;
// Division: divisor, interval: interval
int divisor = 2, interval = len / 2;
while (interval >= 1) {
for (int i = interval; i < len; i++) {
for (int j = i; j >= interval && arr[j] < arr[j - interval]; j -= interval) {
swap(arr, j, j - interval);
}
}
interval /= divisor;
}
}
// Java Version
/**
* Hibbard Increment: 1, 3, 7
* General term formula: 2^k - 1
* @param arr Array to be sorted
*/
public void shellSort2(int[] arr) {
int len = arr.length;
// Division: divisor, interval: interval
int interval = 1, k = 1;
while (1 << k - 1 < len) {
k++;
}
interval = 1 << k - 1;
while (interval >= 1) {
for (int i = interval; i < len; i++) {
for (int j = i; j >= interval && arr[j] < arr[j - interval]; j -= interval) {
swap(arr, j, j - interval);
}
}
k--;
interval = 1 << k - 1;
}
}
// Java Version
/**
* Hibbard Another way to write increment
* General term formula: 2^k - 1
* @param arr Array to be sorted
*/
public void shellSort3(int[] arr) {
int len = arr.length;
// Division: divisor, interval: interval
int divisor = 2, interval = 1;
while (interval < len / divisor) {
interval *= divisor;
interval += 1;
}
while (interval >= 1) {
for (int i = interval; i < len; i++) {
for (int j = i; j >= interval && arr[j] < arr[j - interval]; j -= interval) {
swap(arr, j, j - interval);
}
}
interval /= divisor;
}
}
// Java Version
/**
* Sedgewick Increment: 1, 5, 19, 41
* General term formula: 9 * 4^i − 9 * 2^i + 1 or 4^i - 3 * 2^i + 1, the worst time complexity is O(n^(4/3)), and the average time complexity is O(n^(7/6)).
* @param arr Array to be sorted
*/
public void shellSort3(int[] arr) {
int len = arr.length;
// Division: divisor, interval: interval
int interval = 1, k = 1;
while (9 * ((1 << 2 * k) - (1 << k)) + 1 < len) {
k++;
}
interval = 9 * ((1 << 2 * k) - (1 << k)) + 1;
while (interval >= 1) {
for (int i = interval; i < len; i++) {
for (int j = i; j >= interval && arr[j] < arr[j - interval]; j -= interval) {
swap(arr, j, j - interval);
}
}
k--;
interval = 9 * ((1 << 2 * k) - (1 << k)) + 1;
}
}
Quick sort
Algorithm idea
Quick sort (English: Quicksort), also known as partition exchange sort (English: partition exchange sort).
The algorithm idea of quick sorting is through Divide and conquer To sort an array.
Quick sort is divided into three processes:
- Divide the guarantee relationship into two parts (relative size);
- Recursion to two subsequences for quick sorting;
- There is no need to merge, because the sequence is completely ordered at this time.
The specific process is:
- The first step is to divide the sequence into two parts, and then ensure that the number in the former sub sequence is less than that in the latter sub sequence. In order to ensure the average time complexity, a number m is generally randomly selected as the boundary between the two subsequences.
- After that, maintain the two pointers p and q, and consider whether the current number is placed in the position it should be placed (front or back). If the current number is not right, for example, if the following pointer q encounters a number smaller than m, you can exchange the numbers at p and q, and then move p back one bit. After all the positions of the current number are aligned, move the pointer to continue processing until the two pointers meet.
- At this time, the sequence has been ordered separately, and the number in the first sequence is less than the second number, so it's good to splice it directly.
It should be noted that, in fact, quick sort does not specify how to implement the first step. There are more than one implementation method in both the process of selecting m and the process of dividing.
stability
Quick sort is an unstable sort algorithm.
Time complexity
The optimal time complexity and average time complexity are O(nlogn) and the worst time complexity is (n^2).
code implementation
// Java Version
/**
* Quick sort, also known as partition exchange sort
* @param arr Array to be sorted
*/
public void quickSort(int[] arr) {
quickSort(arr, 0, arr.length - 1);
}
/**
* Update low every time it is executed to ensure that the number in the left column of the element with the subscript position of low is less than or equal to the number in the right column
* @param arr Array to be sorted
* @param left Left boundary
* @param right Right boundary
*/
public void quickSort(int[] arr, int left, int right) {
// Recursive end condition
if (left >= right) {
return;
}
// Based on the leftmost element,
int midValue = arr[left];
int low = left, high = right;
while (low < high) {
// The positions of the two while cannot be exchanged. You must update the high pointer first and then the low pointer
while (low < high && arr[high] >= midValue) {
high--;
}
while (low < high && arr[low] <= midValue) {
low++;
}
if (low < high) {
swap(arr, low, high);
}
}
swap(arr, left, low);
quickSort(arr, left, low - 1);
quickSort(arr, low + 1, right);
}
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
optimization
Heap sort
Algorithm idea
Heap sort (English: Heapsort) refers to the use of Binary reactor This data structure is designed by a sort algorithm.
The sorting process is as follows (take ascending sorting as an example):
-
Firstly, the large top heap is established, and then the elements at the top of the heap are taken out as the maximum value, exchanged with the elements at the end of the array, and the nature of the residual heap is maintained;
-
Then take out the elements at the top of the heap as the next largest value, exchange with the penultimate element of the array, and maintain the nature of the residual heap;
-
By analogy, after the n - 1 operation, the entire array is sorted.
stability
Like selective sorting, it is an unstable sorting algorithm because it includes the operation of exchanging positions.
Time complexity
The optimal time complexity, average time complexity and worst time complexity of heap sorting are O(nlogn).
code implementation
/**
* Heap sort is a kind of selective sort. Its worst and best, average time complexity is O(nlogn), and it is also an unstable sort.
* In ascending order, the maximum heap is used; In descending order, the smallest heap is used
* @param arr Array to be sorted
*/
public void heapSort(int[] arr) {
int len = arr.length;
// Start heap from the last parent node (from bottom to top) and sift down to complete heap (heap, construct the maximum heap)
// If i is the subscript value of the parent node, the subscript values of the left and right nodes are [i * 2 + 1] and [i * 2 + 2] respectively
// If the array size is an odd value, the maximum subscript value (len - 1) is an even number [i * 2 + 2]. At this time, i can be obtained from (len - 1 - 1) / 2
// If the array size is an even value, the maximum subscript value (len - 1) is an odd number [i * 2 + 1]. At this time, i can also be obtained from (len - 1 - 1) / 2
for (int i = (len - 2) / 2; i >= 0; i--) {
siftDown(arr, i, len - 1);
}
// At this point: arr [i] > = arr [I * 2 + 1] & & arr [i] > = arr [I * 2 + 2]
// First, exchange the first element with the previous element that has been arranged, and then readjust (the element before the element just adjusted) until sorting is completed
for (int i = len - 1; i > 0; i--) {
// Swap the heap top element arr[0] with the following element arr[i], so that arr[i] is the maximum value in the unordered part arr[0...i]
swap(arr, 0, i);
// Update the heap top element, even if the heap top element is the maximum value in the unsorted part arr[0...i]
siftDown(arr, 0, i - 1);
}
}
private void siftDown(int arr[], int start, int end) {
// Calculate the subscript of the parent node and the left child node
int parent = start;
int child = parent * 2 + 1;
// Only when the subscript of the child node is within the range can the comparison be made
while (child <= end) {
// First, compare the size of the two child nodes and select the largest one
if (child + 1 <= end && arr[child] < arr[child + 1]) {
child++;
}
// If the parent node is larger than the child node, it means that the adjustment is completed and the function will jump out directly
if (arr[parent] >= arr[child]) {
return;
}
// Otherwise, the parent-child content is exchanged, and the child nodes are compared with the grandchildren
else {
swap(arr, parent, child);
parent = child;
child = parent * 2 + 1;
}
}
}
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
Merge sort
Algorithm idea
Merge sort (English: merge sort) is a kind of Divide and conquer Thought sorting algorithm.
Merging and sorting is divided into three steps:
- Divide the sequence into several groups. At first, each number is a group;
- Merge several groups in pairs and ensure that the merged groups are orderly;
- Recursively proceed to the second step until the last group is left.
The first two steps of merging and sorting are well realized. The key is how to merge the two subsequences. Note that the two subsequences have been guaranteed to be orderly in the second step. In the third step, we actually want to combine the two ordered sequences.
The difference between merge sort and quick sort is that quick sort is performed recursively after sorting in a large range. Merge sort is performed recursively after sorting in the minimum range. The difference in code is that the recursion of quick sort is written behind the sorting logic, and the recursion of merge sort is written in front of the sorting logic.
stability
Merge sort is a stable sort algorithm.
Time complexity
The optimal time complexity, average time complexity and worst time complexity of merging and sorting are O(nlogn).
Spatial complexity
The space complexity of merging and sorting is O(n).
code implementation
/**
* Merge sort
* Its optimal time complexity, average time complexity and worst time complexity are O(nlogn); The space complexity is O(n).
* @param arr Array to be sorted
*/
public void mergeSort(int[] arr) {
int len = arr.length;
mergeSort(arr, 0, len - 1, new int[len]);
}
/**
* The real implementation part of merge sort is used to sort the number of the interval of arr array [left, right].
* @param arr Array to be sorted
* @param left Left boundary
* @param right Right boundary
* @param temp Auxiliary array is used to temporarily store ordered versions. It is created at one time and reused indefinitely.
*/
private void mergeSort(int[] arr, int left, int right, int[] temp) {
// Recursion does not begin to perform merge sorting until each number is a group
if (right <= left) {
return;
}
// Mid is the right boundary of the left array, and mid + 1 is the left boundary of the right array
int mid = left + (right - left >> 1);
mergeSort(arr, left, mid, temp);
mergeSort(arr, mid + 1, right, temp);
// p: Pointer in left array, q: pointer in right array, s: pointer in auxiliary array
int p = left, q = mid + 1, s = left;
while (s <= right) {
// If the elements of the right array are selected or the elements of the left array are smaller than those of the right array
if (q > right || (p <= mid && arr[p] < arr[q])) {
// Select the elements in the left array
temp[s++] = arr[p++];
} else {
// Select the element in the array on the right
temp[s++] = arr[q++];
}
}
for (int i = left; i <= right; i++) {
arr[i] = temp[i];
}
}
Count sort
Algorithm principle
Counting sort (English: counting sort) is a linear time sorting algorithm, which is suitable for the case where the value range of the data to be sorted is small.
The working principle of counting sorting is to use an additional array C, where the ith element is the number of elements with A value equal to i in the array A to be sorted, and then arrange the elements in A to the correct position according to array C.
Its working process is divided into three steps:
- Each number is calculated several times;
- Find the number of occurrences of each number Prefix and;
- Using the prefix sum of the number of occurrences, the ranking of each number is calculated from right to left.
stability
Counting sorting is a stable sorting algorithm.
Time complexity
The time complexity of counting sorting is O(n + w), where w represents the value range size of the data to be sorted.
Spatial complexity
The spatial complexity of counting sorting is O(w), where w represents the size of the value range of the data to be sorted.
code implementation
/**
* Count sort
* The time complexity of counting sorting is O(n + w), where w represents the value range size of the data to be sorted.
* The spatial complexity of counting sorting is O(w), where w represents the size of the value range of the data to be sorted.
* @param arr Array to be sorted
*/
public void countingSort(int[] arr) {
int len = arr.length;
int maxValue = Integer.MIN_VALUE, minValue = Integer.MAX_VALUE;
// Find the maximum and minimum values in the array to be sorted
for (int i = 0; i < len; i++) {
maxValue = Math.max(maxValue, arr[i]);
minValue = Math.min(minValue, arr[i]);
}
// The range of cnt storage is [minValue, maxValue]
int[] cnt = new int[maxValue - minValue + 1], temp = new int[len];
for (int i = 0; i < len; i++) {
cnt[arr[i] - minValue]++;
}
// Prefix and number of occurrences
for (int i = 1; i <= maxValue - minValue; i++) {
cnt[i] += cnt[i - 1];
}
for (int i = 0; i < len; i++) {
// cnt[arr[i] - minValue] indicates the prefix and number of occurrences corresponding to the subscript value
temp[--cnt[arr[i] - minValue]] = arr[i];
}
for (int i = 0; i < len; i++) {
arr[i] = temp[i];
}
}
Bucket sorting
Algorithm principle
Bucket sort (English: bucket sort) is a sort algorithm, which is suitable for the situation that the value range of the data to be sorted is large but the distribution is relatively uniform.
Bucket sorting is carried out according to the following steps:
- Newly created (maxValue - minValue) / len + 1 array as empty bucket;
- Traverse the sequence and put the elements into the corresponding bucket one by one;
- Sort each bucket that is not empty;
- Put the elements back into the original sequence from the bucket that is not empty.
stability
The stability of bucket sorting depends on the stability of inner sorting.
Since there are few elements in each block, insertion sorting is generally used. At this time, bucket sorting is a stable sorting algorithm.
Time complexity
The average time complexity of bucket sorting is O(n + n^2 / k + k) (dividing the value range into n blocks + sorting + re merging elements). When k ≈ n, it is O(n).
The worst time complexity of bucket sorting is O(n^2).
code implementation
/**
* Bucket sorting
* @param arr Array to be sorted
*/
public void bucketSort(int[] arr) {
int len = arr.length;
int minValue = Integer.MAX_VALUE, maxValue = Integer.MIN_VALUE;
// Find the maximum and minimum values in the array to be sorted
for (int i = 0; i < len; i++) {
maxValue = Math.max(maxValue, arr[i]);
minValue = Math.min(minValue, arr[i]);
}
// Calculate the number of barrels
int bucketSize = (maxValue - minValue) / len + 1;
List<List<Integer>> buckets = new ArrayList<>(bucketSize);
// Initialize each bucket
for (int i = 0; i < bucketSize; i++) {
buckets.add(new ArrayList<>());
}
//Put the corresponding element into the bucket
for (int i = 0; i < len; i++) {
int diffValue = arr[i] - minValue;
buckets.get(diffValue / len).add(arr[i]);
}
int idx = 0;
for (int i = 0; i < bucketSize; i++) {
// Insert and sort each bucket in turn
insertionSort(buckets.get(i));
// Update the sorted bucket elements to the original array
for (int j = 0; j < buckets.get(i).size(); j++) {
arr[idx++] = buckets.get(i).get(j);
}
}
}
/**
* Insert sort
* @param bucket Bucket to be sorted
*/
private void insertionSort(List<Integer> bucket) {
for (int i = 1; i < bucket.size(); i++) {
int key = bucket.get(i);
int j = i - 1;
while (j >= 0 && bucket.get(j) > key) {
bucket.set(j + 1, bucket.get(j));
j--;
}
bucket.set(j + 1, key);
}
}
Cardinality sort
Algorithm implementation
Radix sort is a non comparative sort algorithm, which was first used to solve the problem of card sorting.
Its working principle is to split the elements to be sorted into k keywords (when comparing two elements, first compare the first keyword, if the same, then compare the second keyword...), then sort the K keyword stably, and then sort the k - 1 keyword stably, Then sort the k - 2 keyword stably... Finally sort the first keyword stably, so as to complete the stable sorting of the whole sequence to be sorted.
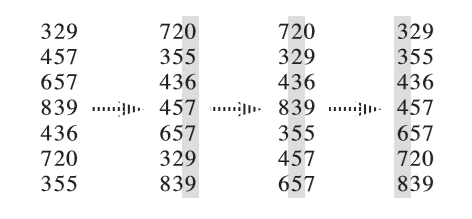
Cardinality sorting needs a stable algorithm to complete the internal sorting of keywords.
In general, cardinal sorting is faster than comparison based sorting algorithms, such as quick sorting. However, due to the need for additional memory space, when memory space is scarce, in-situ replacement algorithm (such as quick sorting) may be a better choice.
stability
Cardinality sorting is a stable sorting algorithm.
Time complexity
Generally speaking, if the value range of each keyword is not large, it can be used Count sort As an inner layer sort, the complexity at this time is 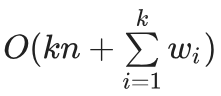
Where wi is the value range size of the ith keyword. If the keyword value range is large, you can directly use comparison based O(nklogn) sorting instead of cardinality sorting.
Spatial complexity
The spatial complexity of cardinality sorting is O(n + k).
code implementation
/**
* Cardinality sort
* @param arr Array to be sorted
*/
public void radixSort(int[] arr) {
int len = arr.length;
int maxValue = Integer.MIN_VALUE;
// Find the maximum and minimum values in the array to be sorted
for (int i = 0; i < len; i++) {
maxValue = Math.max(maxValue, arr[i]);
}
for (int exp = 0; maxValue / exp == 0; exp *= 10) {
// A temporary array that stores elements to be queued
int[] temp = new int[len];
// Number of barrels
int[] buckets = new int[10];
// Store the number of data occurrences in buckets
for (int value : arr) {
// (value / exp)% 10: bottom of value
buckets[(value / exp) % 10]++;
}
// The "value range" of the elements in each bucket is small, and the internal sorting uses counting sorting
countingSort(arr, buckets, temp, exp);
// Assign the ordered element temp to arr
System.arraycopy(temp, 0, arr, 0, len);
}
}
private void countingSort(int[] arr, int[] buckets, int[] temp, int exp) {
// Change buckets[i],
for (int i = 1; i < 10; i++) {
buckets[i] += buckets[i - 1];
}
// Store the data in the temporary array temp
for (int i = arr.length - 1; i >= 0; i--) {
temp[buckets[(arr[i] / exp) % 10] - 1] = arr[i];
buckets[(arr[i] / exp) % 10]--;
}
}