✨ Algorithm series recommended:
- LeetCode clearance: I heard that the linked list is the threshold, so I raised my foot and crossed the door
- Interview brush algorithm, these APIs can not be known!
- LeetCode clearance: array seventeen, really not simple
- LeetCode clearance: Brush 39 binary trees, crazy!
Hello, I'm the third, a programmer who can't brush the algorithm. Although there are not many questions related to sorting algorithm in the force buckle, you have to tear them up in the interview. Next, let's take a look at the ten basic sorts.
Sorting basis
Stability of sorting algorithm
What is the stability of sorting algorithm?
When the keywords of the records to be sorted are different, the sorting result is unique, otherwise the sorting result is not unique [1].
If there are multiple records with the same keyword in the file to be sorted, the relative order between these records with the same keyword remains unchanged after sorting, and the sorting method is stable:
If the relative order of records with the same keyword changes, this sorting method is said to be unstable.
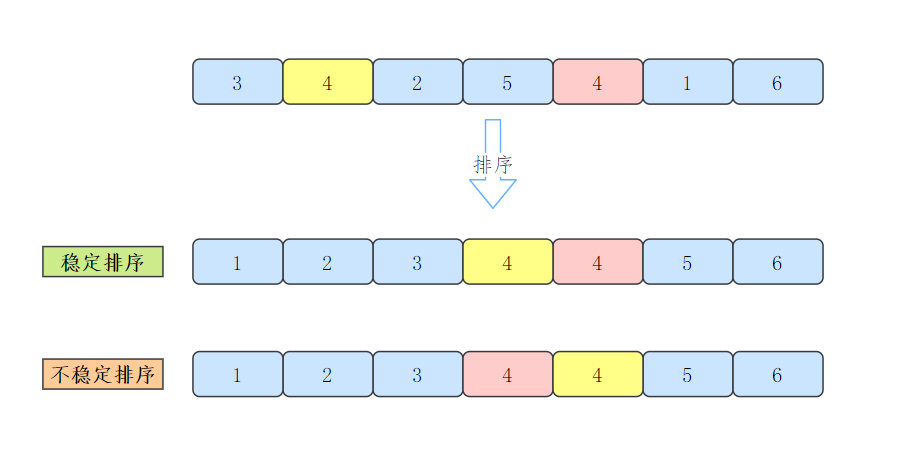
The stability of the sorting algorithm is for all input instances. That is, in all possible input instances, as long as one instance makes the algorithm not meet the stability requirements, the sorting algorithm is unstable.
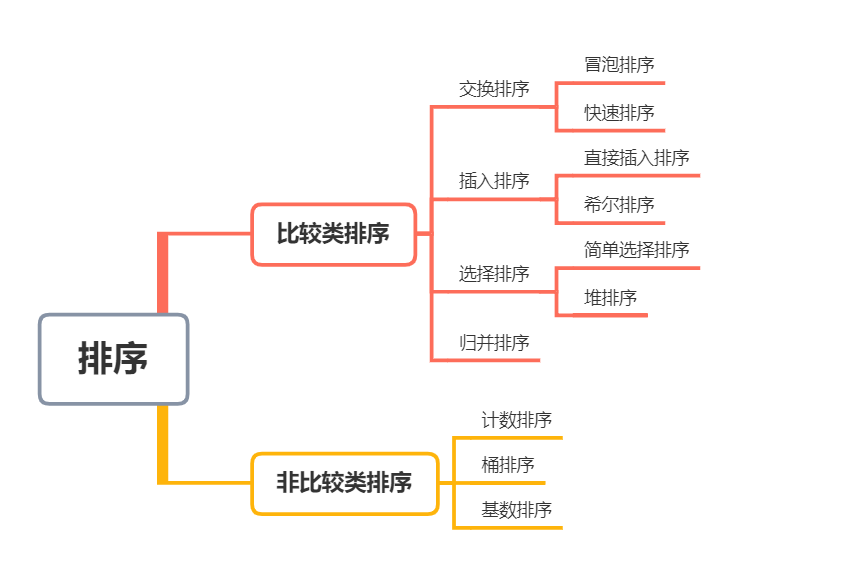
Sorted classification
Sorting can be divided into two categories: internal sorting and external sorting.
According to whether the relative order between elements is determined by comparison, sorting can be divided into comparison sort and non comparison sort.
Bubble sorting
Bubble sorting principle
Persimmon pick soft pinch, first from the simplest start.
Bubble sorting has a nice name and the best understanding idea.
The basic idea of bubble sorting is to traverse from one end to the other, compare the sizes of adjacent elements, and exchange if it is in reverse order.
The dynamic diagram is as follows (source reference [4]):
Simple code implementation
First, simply implement the following, very simple, two-layer loop and comparison of adjacent elements:
public void sort(int[] nums) {
for (int i = 0; i < nums.length; i++) {
for (int j = i + 1; j < nums.length; j++) {
//Ascending order
if (nums[i] > nums[j]) {
//exchange
int temp = nums[i];
nums[j] = nums[i];
nums[i] = temp;
}
}
}
}
Bubble sorting optimization
There is still a problem with the above code implementation. What is the problem?
Even if the array is ordered, it will continue to traverse.
Therefore, a flag bit can be used to mark whether the array is orderly. If it is orderly, it will jump out of traversal.
public void sort(int[] nums) {
//Flag bit
boolean flag = true;
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < nums.length - i - 1; j++) {
//Ascending order
if (nums[j] > nums[j + 1]) {
//exchange
int temp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = temp;
}
}
//If ordered, end the loop
if (flag) {
break;
}
}
}
Performance analysis of bubble sorting
Elements of the same size do not exchange positions, so bubble sorting is stable.
| Algorithm name | Best time complexity | Worst time complexity | Average time complexity | Spatial complexity | Is it stable |
|---|---|---|---|---|---|
| Bubble sorting | O(n) | O(n²) | O(n²) | O(1) | stable |
Select sort
Selective sorting principle
Why is selective sorting called selective sorting? What is the principle?
Its idea: first find the smallest or largest element in the unordered sequence and put it at the beginning of the sorted sequence, then relay from the unordered sequence to continue to find the smallest or largest element, and then put it at the end of the sorted sequence. And so on until all elements are sorted.
The dynamic diagram is as follows (source reference [4]):
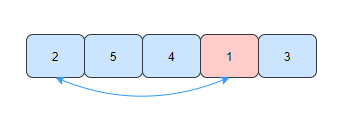
Let's take an example to sort the array by selective sorting [2,5,4,1,3].
- For the first time, find the smallest element 1 in the array and exchange its position with the first element of the array.
- The second time, find the smallest element 2 in the unordered elements and exchange positions with the second element of the array.
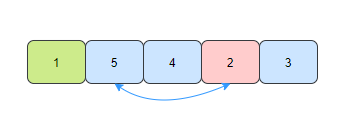
- The third time, find the smallest element 3 in the unordered elements, and exchange positions with the third element of the array.
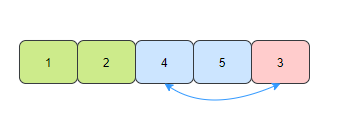
- The fourth time, find the smallest element 4 in the unordered elements, and exchange positions with the fourth element of the array.
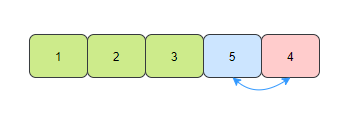
So here, our array is ordered.
Select Sorting code implementation
The idea of selecting sorting is very simple and not difficult to implement.
public void sort(int[] nums) {
int min = 0;
for (int i = 0; i < nums.length - 1; i++) {
for (int j = i + 1; j < nums.length; j++) {
//Find the smallest number
if (nums[j] < min) {
min = j;
}
}
//exchange
int temp = nums[i];
nums[i] = nums[min];
nums[min] = temp;
}
}
Select sort performance analysis
Is the sorting stable?
The answer is unstable because after finding the minimum value in the unordered sequence, it is exchanged with the end element of the sorted sequence.
| Algorithm name | Best time complexity | Worst time complexity | Average time complexity | Spatial complexity | Is it stable |
|---|---|---|---|---|---|
| Select sort | O(n²) | O(n²) | O(n²) | O(1) | instable |
Insert sort
Insert sort principle
There is a very vivid metaphor for insertion sorting. Landlords - the cards we touch are chaotic. We will insert the cards we touch in the right place.
Its idea: insert an element into the ordered sequence, so as to get a new ordered sequence.
The dynamic diagram is as follows (source reference 3):
Take the array [2,5,4,1,3] as an example:
- First pass: insert element 5 into the appropriate position of the sorted sequence from the unordered sequence

- The second time: then insert element 4 into the sorted sequence in the unordered sequence. You need to traverse the ordered sequence to find the appropriate position

- Third trip: continue, insert 1 into the appropriate position

- Fifth trip: continue, insert 3 into the appropriate position

OK, the sorting is over.
Insert sort code implementation
Find the location of the inserted element and move other elements.
public void sort(int[] nums) {
//The unordered sequence starts with 1
for (int i = 1; i < nums.length; i++) {
//An ordered sequence of elements needs to be inserted
int value = nums[i];
int j = 0;
for (j = i - 1; j >= 0; j--) {
//mobile data
if (nums[j] > value) {
nums[j + 1] = nums[j];
} else {
break;
}
}
//Insert element
nums[j + 1] = value;
}
}
Insert sort performance analysis
Insert sort moves elements larger than insert elements, so the relative position of the same elements remains unchanged and is stable.
From the code, we can see that if the appropriate location is found, there will be no comparison, so the best time complexity is O(n).
| Algorithm name | Best time complexity | Worst time complexity | Average time complexity | Spatial complexity | Is it stable |
|---|---|---|---|---|---|
| Insert sort | O(n) | O(n²) | O(n²) | O(1) | stable |
Shell Sort
Hill sorting principle
Hill sort, the name comes from its inventor Shell. It is an improved version of direct insertion sorting.
The idea of hill sorting is to divide the whole record sequence to be sorted into several subsequences for insertion sorting.
We know that direct insertion sort is not ideal in the face of a large number of disordered data. Hill sort is to achieve the basic order of array elements by jumping, and then use direct insertion sort.
Hill sort dynamic chart (dynamic chart source reference [1]):

Let's take the array [2,5,6,1,7,9,3,8,4] as an example to see the hill sorting process:
- The number of array elements is 9, and 7 / 2 = 4 is taken as the subscript difference. The elements with subscript difference of 4 are divided into a group

- Insert and sort within the group to form an ordered sequence
- Then take 4 / 2 = 2 as the subscript difference, and divide the elements with subscript difference of 2 into a group

- Insert sorting within the group to form an ordered sequence
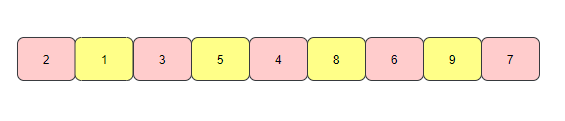
- Subscript difference = 2 / 2 = 1, insert the remaining elements into the sort
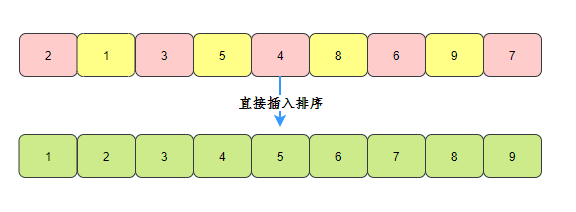
Hill sorting code implementation
You can look at the previous insert sort, Hill sort
Just a direct insertion sort with step size.
public void sort(int[] nums){
//Subscript difference
int step=nums.length;
while (step>0){
//This is optional or 3
step=step/2;
//Group for insertion sort
for (int i=0;i<step;i++){
//Elements within a group, starting with the second
for (int j=i+step;j<nums.length;j+=step){
//Element to insert
int value=nums[j];
int k;
for (k=j-step;k>=0;k-=step){
if (nums[k]>value){
//Move elements within a group
nums[k+step]=nums[k];
}else {
break;
}
}
//Insert element
nums[k+step]=value;
}
}
}
}
Hill sorting performance analysis
- Stability analysis
Hill sort is a deformation of direct insertion sort, but unlike direct insertion sort, it is grouped, so the relative positions of the same elements in different groups may change, so it is unstable.
- Time complexity analysis
The time complexity of hill sorting is related to the selection of incremental sequence. The range is O(n^(1.3-2)). The time complexity of previous sorting algorithms is basically O(n) ²), Hill sorting is one of the first algorithms to break through this time complexity.
| Algorithm name | Time complexity | Spatial complexity | Is it stable |
|---|---|---|---|
| Shell Sort | O(n^(1.3-2)) | O(1) | instable |
Merge sort
Merge sort principle
Merge sort is an effective sort algorithm based on merge operation. Merge means merge. The definition of data structure is to merge several ordered sequences into a new ordered sequence.
Merge sort is a typical application of divide and conquer. What does divide and conquer mean? It is to decompose a big problem into several small problems to solve.
The step of merging and sorting is to divide an array into two, then recurse until a single element, and then merge. A single element is merged into a small array, and the decimals are combined into a large array.
The dynamic diagram is as follows (source reference [4]):
Let's take the array [2,5,6,1,7,3,8,4] as an example to see the merging and sorting process:
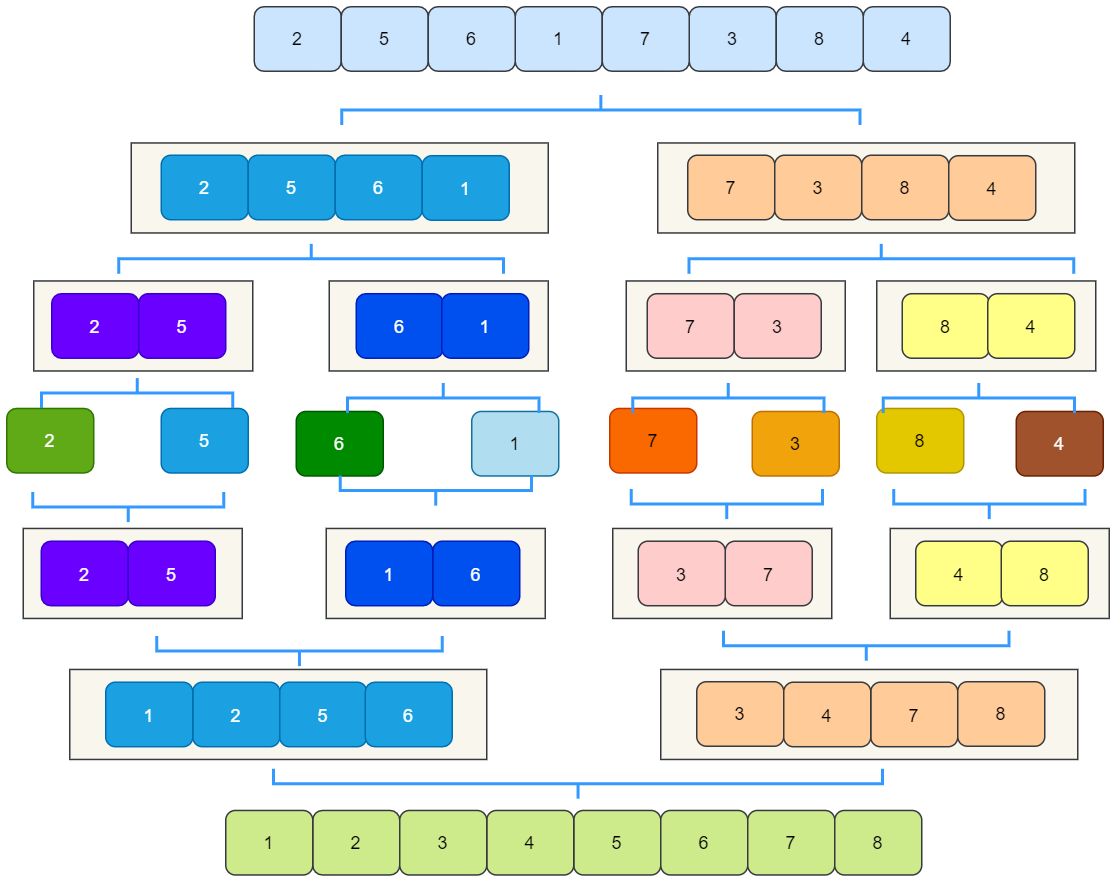
There's no need to talk about splitting. Let's see how to merge.
Merge sort code implementation
Here, recursive sorting is used to realize merging and sorting:
- Recursive termination condition
Recursive start position is less than end position
- Recursive return result
The array sequence passed in is sorted directly, so there is no return value
- Recursive logic
Divide the current array into two groups, decompose them respectively, and finally merge them
The code is as follows:
public class MergeSort {
public void sortArray(int[] nums) {
sort(nums, 0, nums.length - 1);
}
/**
* Merge sort
*
* @param nums
* @param left
* @param right
*/
public void sort(int[] nums, int left, int right) {
//Recursive end condition
if (left >= right) {
return;
}
int mid = left + (right - left) / 2;
//Recursive left half of current sequence
sort(nums, left, mid);
//Recursion of the right half of the current sequence
sort(nums, mid + 1, right);
//Merging result
merge(nums, left, mid, right);
}
/**
* Merge
*
* @param arr
* @param left
* @param mid
* @param right
*/
public void merge(int[] arr, int left, int mid, int right) {
int[] tempArr = new int[right - left + 1];
//Left first subscript and right first subscript
int l = left, r = mid + 1;
int index = 0;
//Move the smaller number to the new array first
while (l <= mid && r <= right) {
if (arr[l] <= arr[r]) {
tempArr[index++] = arr[l++];
} else {
tempArr[index++] = arr[r++];
}
}
//Move the remaining number of the left array into the array
while (l <= mid) {
tempArr[index++] = arr[l++];
}
//Move the remaining number on the right into the array
while (r <= right) {
tempArr[index++] = arr[r++];
}
//Assign the value of the new array to the original array
for (int i = 0; i < tempArr.length; i++) {
arr[i+left] = tempArr[i];
}
}
}
Performance analysis of merge sort
- Time complexity
For a merge, we need to traverse the sequence to be sorted, and the time complexity is O(n).
In the process of merging and sorting, the array needs to be continuously divided into two parts. The time complexity is O(logn).
Therefore, the time complexity of merge sorting is O(nlogn).
- Spatial complexity
A temporary array is used to store the merged elements, with space complexity O(n).
- stability
Merge sort is a stable sort method.
| Algorithm name | Best time complexity | Worst time complexity | Average time complexity | Spatial complexity | Is it stable |
|---|---|---|---|---|---|
| Merge sort | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | stable |
Quick sort
Quick sort principle
Quick sorting is the most frequent sorting algorithm for interview.
Like the merge sort above, quick sort is based on the idea of partition and rule. The general process is as follows:
- Select a reference number, and the reference value generally takes the leftmost element of the sequence
- Reorder the sequence. Those smaller than the benchmark value are placed on the left of the benchmark value and those larger than the benchmark value are placed on the right of the benchmark value. This is the so-called partition
The quick sort dynamic diagram is as follows:
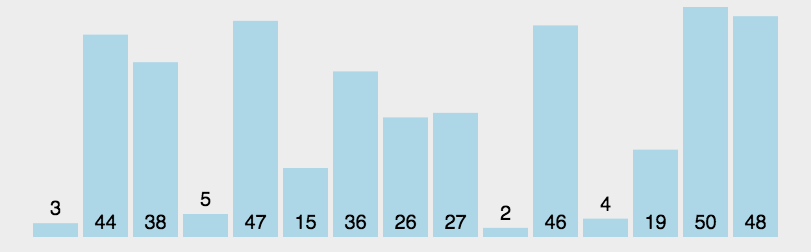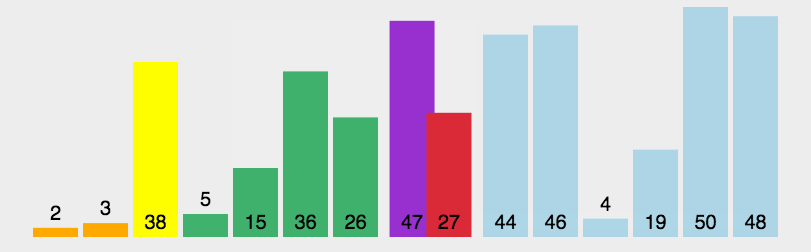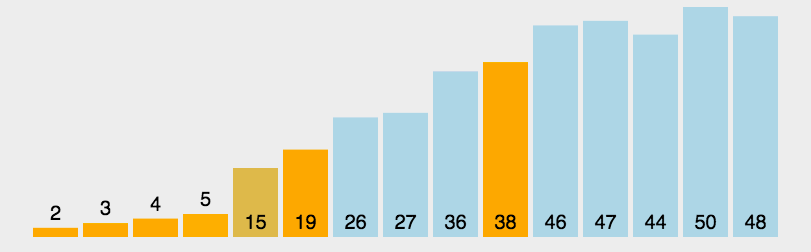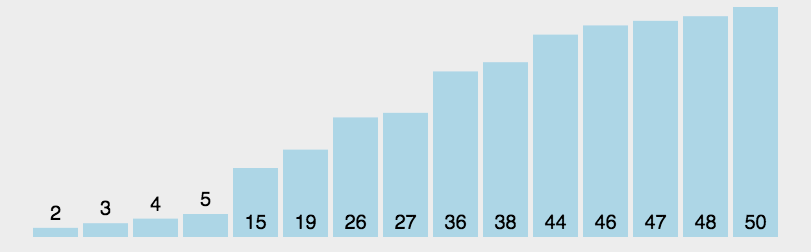
Let's look at a complete quick sort diagram:
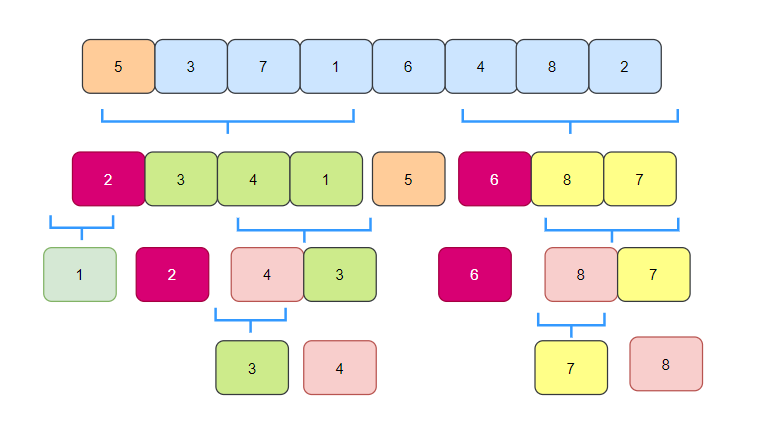
Quick sort code implementation
Single side scan quick sort
Select a number as the reference number pivot, and set a mark mark to represent the rightmost subscript position of the left sequence. Then traverse the array. If the element is greater than the reference value, there is no operation, and continue to traverse. If the element is less than the reference value, mark + 1, and then exchange the element where the mark is located with the element traversed, Mark stores data smaller than the reference value. After traversal, the reference value is exchanged with the element where mark is located.
public class QuickSort0 {
public void sort(int[] nums) {
quickSort(nums, 0, nums.length - 1);
}
public void quickSort(int[] nums, int left, int right) {
//End condition
if (left >= right) {
return;
}
//partition
int partitonIndex = partion(nums, left, right);
//Recursive left partition
quickSort(nums, left, partitonIndex - 1);
//Recursive right partition
quickSort(nums, partitonIndex + 1, right);
}
//partition
public int partion(int[] nums, int left, int right) {
//Reference value
int pivot = nums[left];
//Mark mark initial subscript
int mark = left;
for (int i = left + 1; i <= right; i++) {
if (nums[i] < pivot) {
//If it is less than the reference value, mark+1 and exchange positions
mark++;
int temp = nums[mark];
nums[mark] = nums[i];
nums[i] = temp;
}
}
//Exchange position between reference value and corresponding element of mark
nums[left] = nums[mark];
nums[mark] = pivot;
return mark;
}
}
Bilateral scan quick sort
There is another method of bilateral scanning.
Select a number as the reference value, and then scan from the left and right sides of the array. First find an element greater than the reference value from left to right, fill it in the right pointer position, and then turn to scan from right to left, find an element less than the reference value, and fill it in the left pointer position.
public class QuickSort1 {
public int[] sort(int[] nums) {
quickSort(nums, 0, nums.length - 1);
return nums;
}
public void quickSort(int[] nums, int low, int high) {
if (low < high) {
int index = partition(nums, low, high);
quickSort(nums, low, index - 1);
quickSort(nums, index + 1, high);
}
}
public int partition(int[] nums, int left, int right) {
//Reference value
int pivot = nums[left];
while (left < right) {
//Scan right to left
while (left < right && nums[right] >= pivot) {
right--;
}
//Find the first element smaller than pivot
if (left < right) nums[left] = nums[right];
//Scan from left to right
while (left < right && nums[left] <= pivot) {
left++;
}
//Find the first element larger than pivot
if (left < right) nums[right] = nums[left];
}
//Place the reference number in the appropriate position
nums[left] = pivot;
return left;
}
}
Performance analysis of quick sort
- Time complexity
The time complexity of quick sort is the same as merge sort, which is O(nlogn), but this is the optimal case, that is, the array can be divided into two sub arrays of similar size every time.
If an extreme case occurs, such as an ordered sequence [5,4,3,2,1], and the benchmark value is 5, it needs to be segmented n-1 times to complete the whole quick sorting process. In this case, the time complexity degrades to O(n) ²).
- Spatial complexity
Quick sort is a sort in place algorithm, and the spatial complexity is O(1).
- stability
The comparison and exchange of fast scheduling are performed by jumping, so fast scheduling is an unstable sorting algorithm.
| Algorithm name | Best time complexity | Worst time complexity | Average time complexity | Spatial complexity | Is it stable |
|---|---|---|---|---|---|
| Quick sort | O(nlogn) | O(n²) | O(nlogn) | O(1) | instable |
Heap sort
Heap sorting principle
Remember our previous simple selection sorting? Heap sort is an upgraded version of simple selection sort.
Before learning heap sorting, what is heap?
Complete binary tree is a classic heap implementation of heap.
Let's first understand what a complete binary tree is.
In short, if the node is dissatisfied, the dissatisfied part can only be on the right side of the last layer.
Let's look at a few examples.
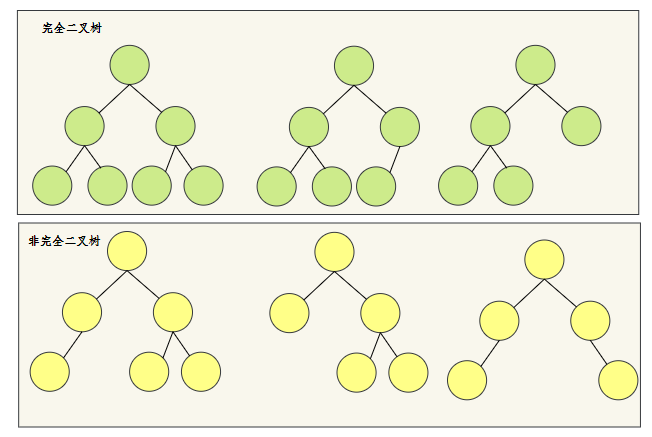
I believe that after reading these examples, we can know what is a complete binary tree and what is a non complete binary tree.
What's that pile?
- Must be a complete binary tree
- The value of any node must be the maximum or minimum value of its subtree
- The maximum value is called "maximum heap", also known as large top heap;
- The minimum value is called "minimum heap", also known as small top heap.
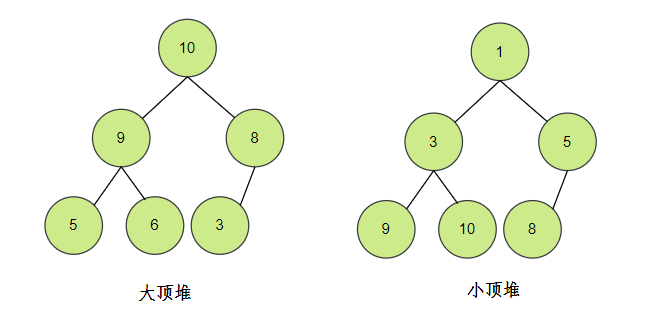
Because the heap is a complete binary tree, the heap can be stored in an array.
The elements are stored in the corresponding position of the array by layer, starting from the subscript 1. Some calculations can be omitted.
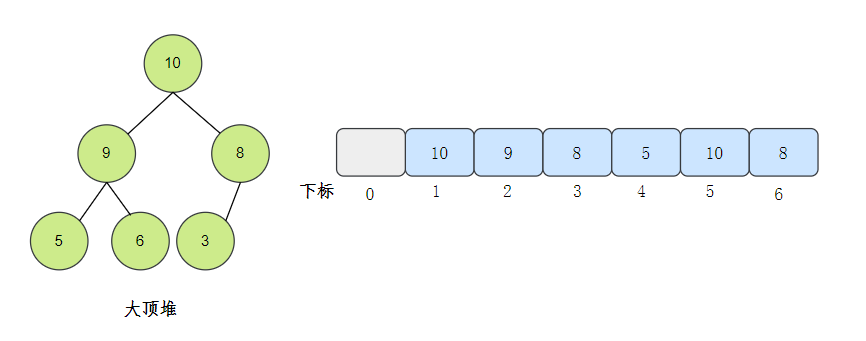
Well, now that we know something about heap, let's take a look at what sort of heap is like? [2]
- Build a large top pile
- Inserts the top of heap element (maximum) at the end of the array
- Let the new largest element float up to the top of the heap
- Repeat the process until the sorting is complete
The dynamic diagram is as follows (source reference [1]):

There are two ways to build a pile, one is to float up and the other is to sink.
What is floating? Is to float the child nodes to the appropriate position layer by layer.
What is sinking? Is to sink the top elements layer by layer to the right position.
The moving picture above uses the way of sinking.
Heap sorting code implementation
public class HeapSort {
public void sort(int[] nums) {
int len = nums.length;
//Build pile
buildHeap(nums, len);
for (int i = len - 1; i > 0; i--) {
//Exchange top and end elements
swap(nums, 0, i);
//Array count length minus 1, hide heap tail element
len--;
//Sink the top element so that the largest element floats to the top
sink(nums, 0, len);
}
}
/**
* Build pile
*
* @param nums
* @param len
*/
public void buildHeap(int[] nums, int len) {
for (int i = len / 2; i >= 1; i--) {
//sink
sink(nums, i, len);
}
}
/**
* Sinking operation
*
* @param nums
* @param index
* @param end
*/
public void sink(int[] nums, int index, int end) {
//Left child node subscript
int leftChild = 2 * index + 1;
//Right child node subscript
int rightChild = 2 * index + 2;
//Node subscript to adjust
int current = index;
//Sinking left subtree
if (leftChild < end && nums[leftChild] > nums[current]) {
current = leftChild;
}
//Sinking right subtree
if (rightChild < end && nums[rightChild] > nums[current]) {
current = rightChild;
}
//If the subscripts are not equal, it proves that they have been exchanged
if (current!=index){
//Exchange value
swap(nums,index,current);
//Continue to sink
sink(nums,current,end);
}
}
public void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
Heap sorting performance analysis
- Time complexity
The time complexity of heap scheduling is the same as that of fast scheduling, which is O(nlogn).
- Spatial complexity
Heap arrangement does not introduce new space, in-situ sorting, and spatial complexity O(1).
- stability
The continuous sinking and exchange of elements at the top of the heap will change the relative position of the same elements, so the heap is unstable.
| Algorithm name | Time complexity | Spatial complexity | Is it stable |
|---|---|---|---|
| Heap sort | O(nlogn) | O(1) | instable |
Count sort
At the beginning of the article, we said that sorting is divided into comparison and non comparison. Counting sorting is a sort method of non comparison.
Counting sort is a sort with linear time complexity. Use space to change time. Let's see how counting sort is realized.
Counting sorting principle
Approximate process of counting sorting [4]:
- Find the largest and smallest elements in the array to be sorted
- Count the number of occurrences of each element with value i in the array and store it in item i of array arr;
- All counts are accumulated (starting from the first element in the arr, and each item is added to the previous item);
- Reverse fill the target array: put each element i in the arr(i) item of the new array, and subtract 1 from arr(i) for each element.
Let's take a look at the dynamic diagram demonstration (from reference [4]):
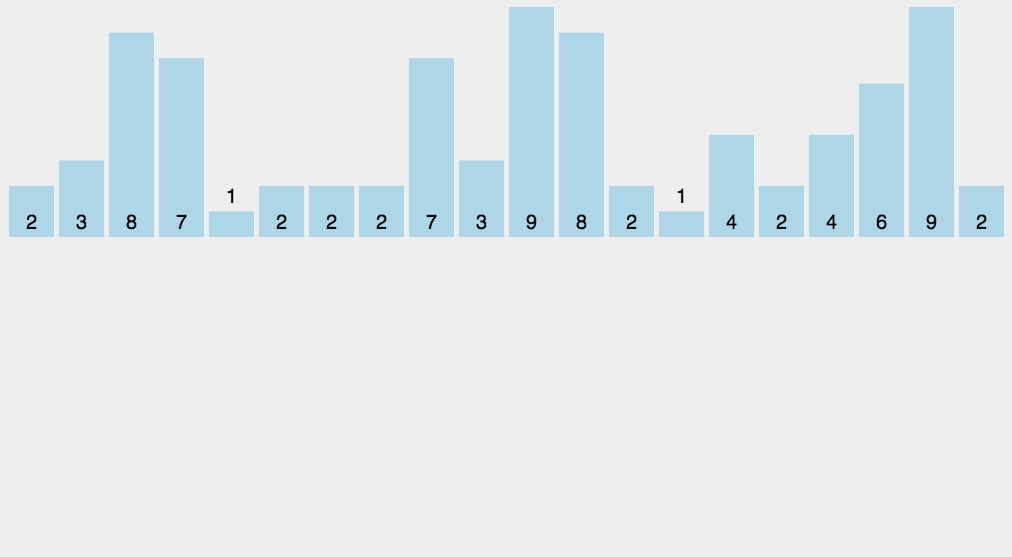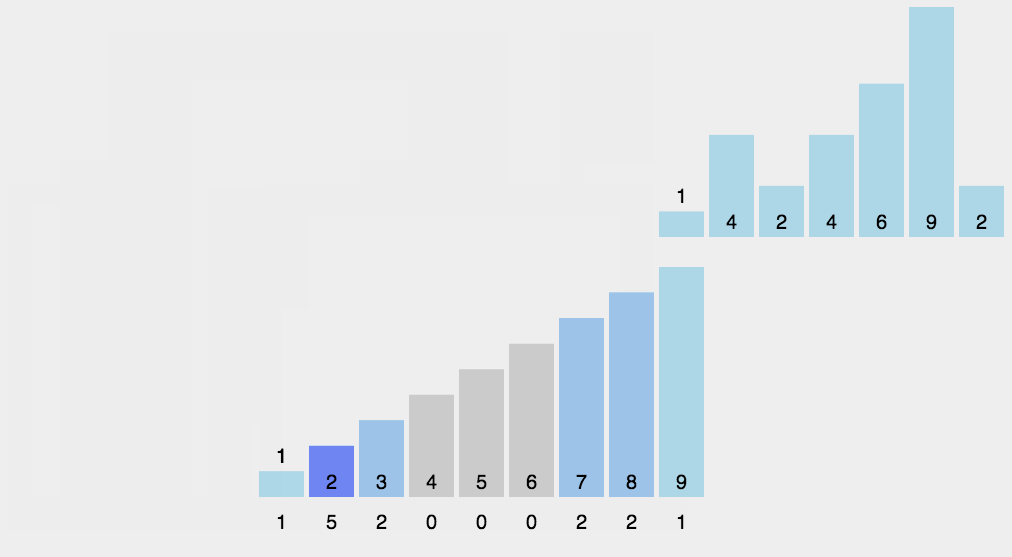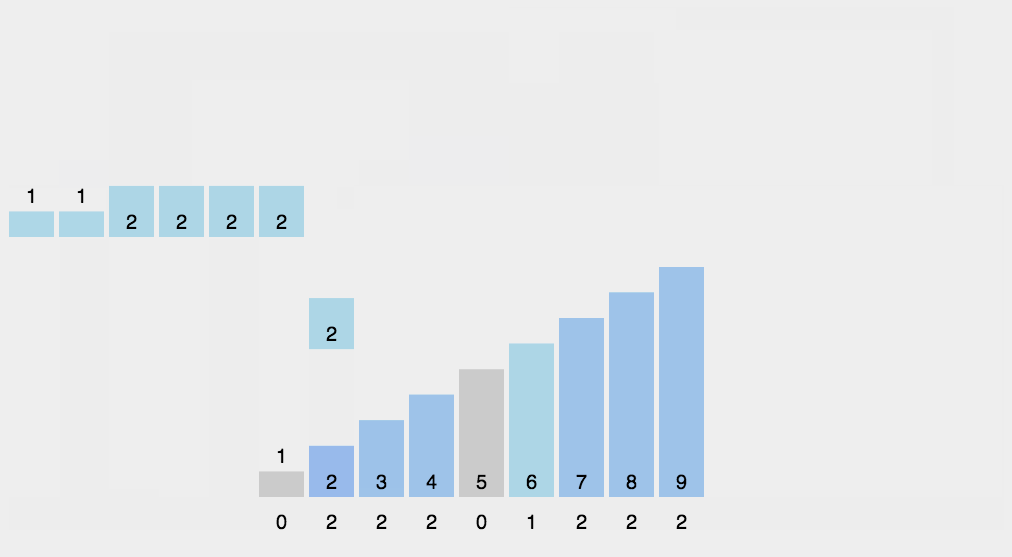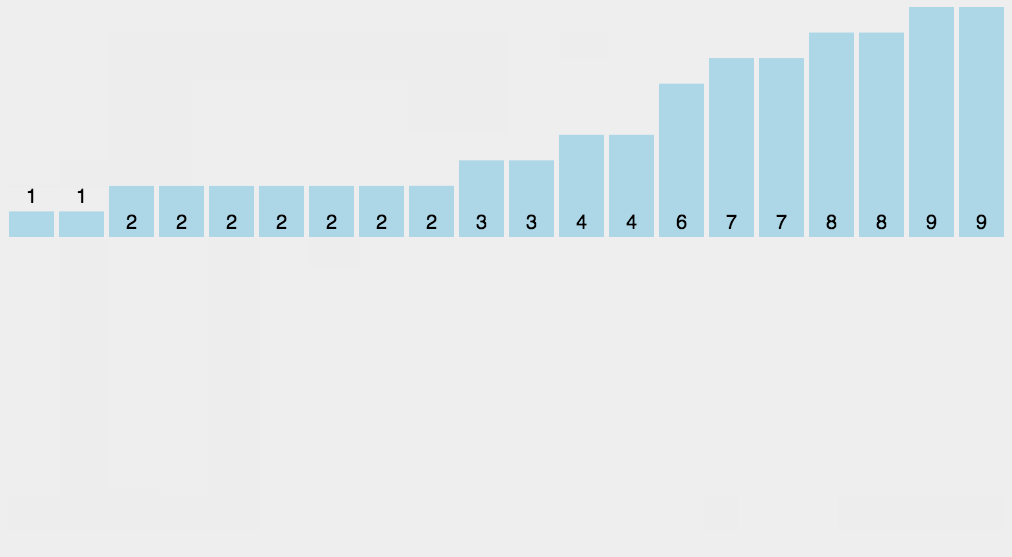
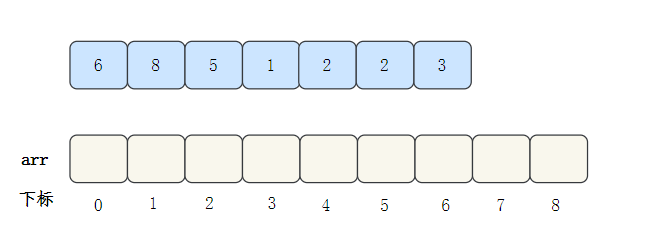
Let's take an array to see the whole process: [6,8,5,1,2,2,3]
- First, find the largest number in the array, that is, 8, and create an empty array arr with a maximum subscript of 8
- Traverse the data and fill the occurrence times of the data into the subscript position corresponding to arr
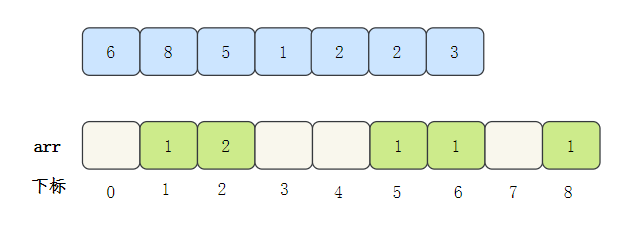
- Then output the subscript value of the array element. If the value of the element is, output it several times
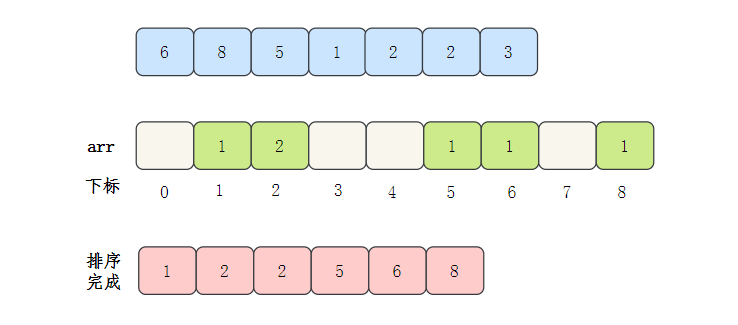
Count sort code implementation
public class CountSort {
public void sort(int[] nums) {
//Find maximum
int max = findMax(nums);
//Create a new array of Statistics
int[] countNums = new int[max + 1];
//Store the number of occurrences of the num element in the corresponding subscript
for (int i = 0; i < nums.length; i++) {
int num = nums[i];
countNums[num]++;
nums[i] = 0;
}
//sort
int index = 0;
for (int i = 0; i < countNums.length; i++) {
while (countNums[i] > 0) {
nums[index++] = i;
countNums[i]--;
}
}
}
public int findMax(int[] nums) {
int max = nums[0];
for (int i = 0; i < nums.length; i++) {
if (nums[i] > max) {
max = nums[i];
}
}
return max;
}
}
OK, at first glance, there is no problem, but when you think about it, there are still some problems. What's the problem?
-
What if the element we want to sort has 0? For example [0,0,5,2,1,3,4], arr is initially 0. How to arrange it?
This is difficult to solve. One way is to add 10 to the original array when counting [- 1,0,2], and then reduce it when sorting and writing back. However, if you happen to encounter the element of - 10, it will be cool.
-
What if the range of elements is large? For example, [9999999999999999], can we apply for an array of 10000 elements?
This can be solved by offset. Find the largest and smallest elements and calculate the offset. For example, [99929999999999], offset = 9999-9992 = 7. We only need to create an array with a capacity of 8.
The version to solve the second problem is as follows:
public class CountSort1 {
public void sort(int[] nums) {
//Find maximum
int max = findMax(nums);
//Find minimum
int min = findMin(nums);
//Offset
int gap = max - min;
//Create a new array of Statistics
int[] countNums = new int[gap + 1];
//Store the number of occurrences of the num element in the corresponding subscript
for (int i = 0; i < nums.length; i++) {
int num = nums[i];
countNums[num - min]++;
nums[i] = 0;
}
//sort
int index = 0;
for (int i = 0; i < countNums.length; i++) {
while (countNums[i] > 0) {
nums[index++] = min + i;
countNums[i]--;
}
}
}
public int findMax(int[] nums) {
int max = nums[0];
for (int i = 0; i < nums.length; i++) {
if (nums[i] > max) {
max = nums[i];
}
}
return max;
}
public int findMin(int[] nums) {
int min = nums[0];
for (int i = 0; i < nums.length; i++) {
if (nums[i] < min) {
min = nums[i];
}
}
return min;
}
}
Performance analysis of counting and sorting
- Time complexity
Our overall number of operations is n+n+n+k=3n+k, so the effort complexity is O(n+k).
- Spatial complexity
The auxiliary array is introduced, and the space complexity is O(n).
- stability
Our implementation is actually unstable, but counting sorting has a stable implementation. You can see reference [1].
At the same time, we also found that count sorting is not suitable for arrays with negative numbers and large element offset values.
Bucket sorting
Bucket array can be regarded as an upgraded version of counting sorting. It divides the elements into several buckets, and the elements in each bucket are sorted separately.
Bucket sorting principle
General process of bucket sorting:
- Set a quantitative array as an empty bucket;
- Traverse the input data and put the elements into the corresponding bucket one by one;
- Sort each bucket that is not empty;
- Splice the ordered data from a bucket that is not empty.
The bucket sorting diagram is as follows (refer to [1] for the source of the diagram):

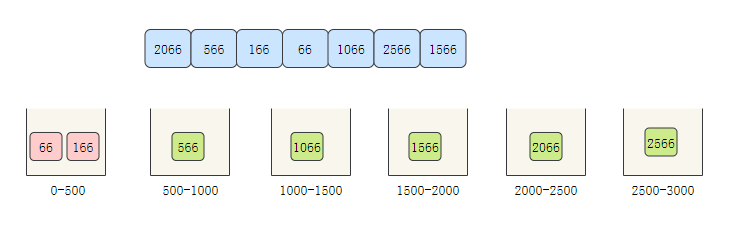
As mentioned above, counting sorting is not suitable for arrays with too large offset. Let's take an array with very large offset [2066566166, 66106625661566] as an example to see the bucket sorting process.
- Create 6 buckets to store 0-500500-10001000-15001500-20002000-25002500-3000 elements respectively
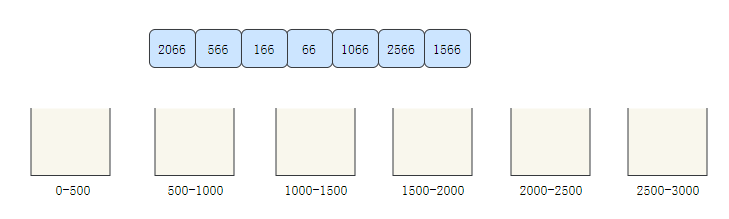
- Traverse the array and allocate the elements to the corresponding bucket
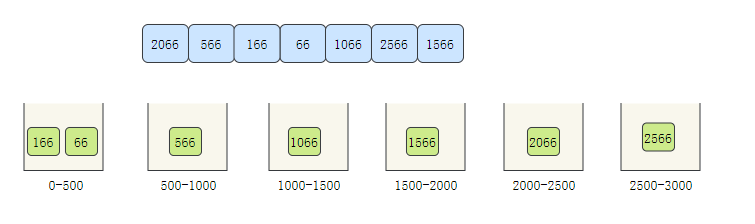
- The elements in the bucket are sorted. Here we obviously only sort the first bucket
- Take out the elements in the bucket in turn, and the elements taken out are orderly
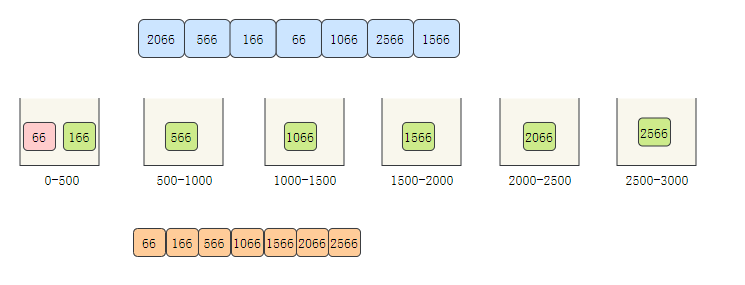
Bucket sorting code implementation
Several problems should be considered for the implementation of bucket sorting:
- How should a bucket be represented?
- How to determine the number of barrels?
- What method is used for sorting in the bucket?
Let's look at the code:
public class BucketSort {
public void sort(int[] nums) {
int len = nums.length;
int max = nums[0];
int min = nums[0];
//Get maximum and minimum values
for (int i = 1; i < len; i++) {
if (nums[i] > max) {
max = nums[i];
}
if (nums[i] < min) {
min = nums[i];
}
}
//time step
int gap = max - min;
//Use list as bucket
List<List<Integer>> buckets = new ArrayList<>();
//Initialization bucket
for (int i = 0; i < gap; i++) {
buckets.add(new ArrayList<>());
}
//Determine the storage range of the bucket
int section = gap / len - 1;
//Array bucket
for (int i = 0; i < len; i++) {
//Determine which bucket the element should be in
int index = nums[i] / section - 1;
if (index < 0) {
index = 0;
}
//Add element to corresponding bucket
buckets.get(index).add(nums[i]);
}
//Sort the elements in the bucket
for (int i = 0; i < buckets.size(); i++) {
//The underlying call is arrays sort
// This api may use three sorts under different circumstances: insert sort, quick sort and merge sort. See [5] for details
Collections.sort(buckets.get(i));
}
//Writes the elements in the bucket to the original array
int index = 0;
for (List<Integer> bucket : buckets) {
for (Integer num : bucket) {
nums[index] = num;
index++;
}
}
}
}
Performance analysis of bucket sorting
- Time complexity
The best case of bucket sorting is that the elements are evenly distributed to each bucket, and the time complexity is O(n). The worst case is that all elements are allocated to one bucket, and the time complexity is O(n) ²). The average time complexity is O(n+k), which is the same as the technical ranking.
- Spatial complexity
For bucket sorting, n additional buckets need to be stored, and k elements need to be stored in the bucket, so the spatial complexity is O(n+k).
- stability
Stability depends on what sort algorithm is used for sorting in the bucket. If the stable sort algorithm is used in the bucket, it is stable. The unstable sorting algorithm is unstable.
Cardinality sort
Cardinality sorting principle
Cardinal sort is a non comparative sort method.
Its basic principle is to cut the elements into different numbers according to the number of bits, and then compare them according to each number of bits.
General process:
- Get the maximum number in the array and get the number of bits;
- arr is the original array, and each bit is taken from the lowest bit to form a radix array
- Count and sort the radix (using the characteristics that count sorting is suitable for a small range of numbers)
The dynamic diagram is as follows (source reference [1]):

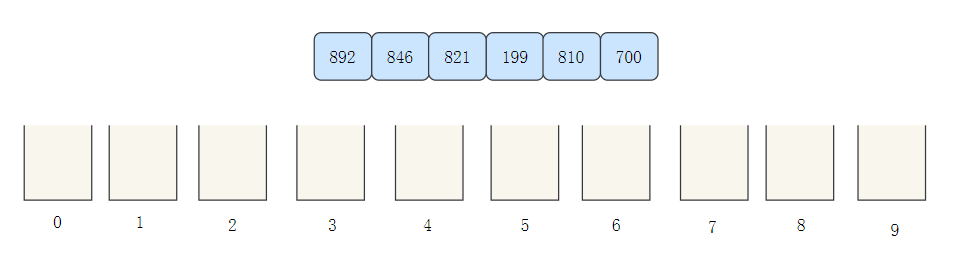
Cardinality sorting can be said to be an evolution of bucket sorting. Let's take [892846821199810700] to see the cardinality sorting process:
- Create ten buckets to store elements
- The elements are allocated to different buckets according to the number of bits
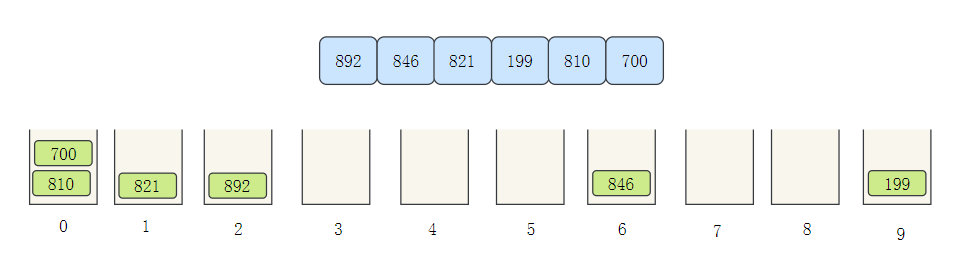
- Then take out the elements in the bucket in turn
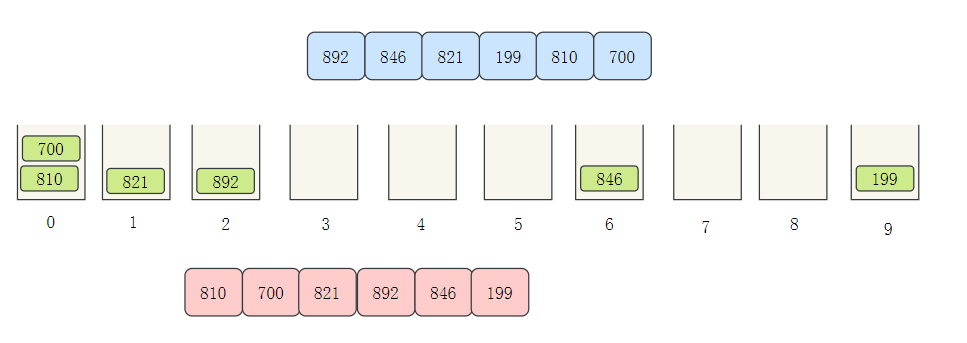
- Next, row ten digits, allocate buckets according to the ten digits, and then take them out in turn
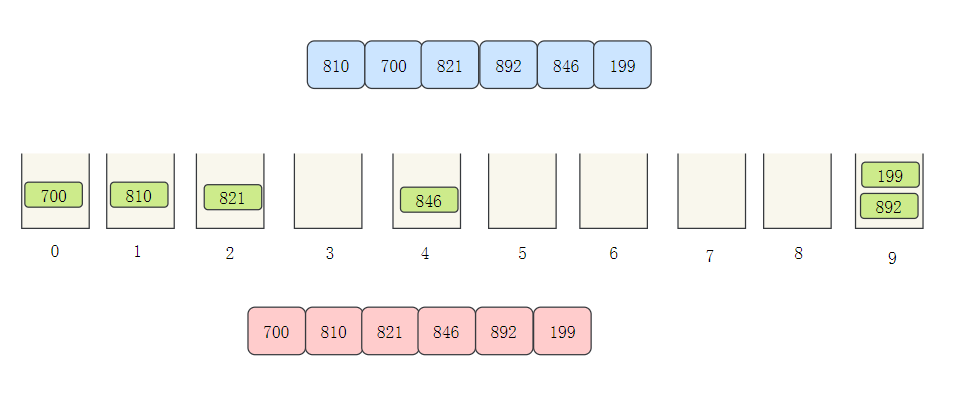
- Next hundred digits
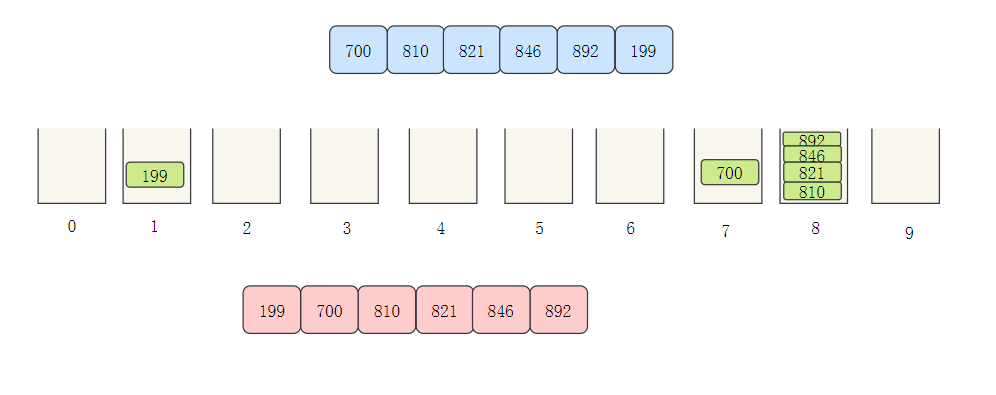
Implementation of cardinality sorting code
public class RadixSort {
public void sort(int[] nums) {
int len = nums.length;
//Maximum
int max = nums[0];
for (int i = 0; i < len; i++) {
if (nums[i] > max) {
max = nums[i];
}
}
//Current sort position
int location = 1;
//Implement bucket with list
List<List<Integer>> buckets = new ArrayList<>();
//Initialize a bucket with size 10
for (int i = 0; i < 10; i++) {
buckets.add(new ArrayList<>());
}
while (true) {
//Maximum number of elements
int d = (int) Math.pow(10, (location - 1));
//Judge whether it is finished
if (max < d) {
break;
}
//Data in bucket
for (int i = 0; i < len; i++) {
//Calculate the remainder and put it into the corresponding bucket
int number = ((nums[i] / d) % 10);
buckets.get(number).add(nums[i]);
}
//Writeback array
int nn = 0;
for (int i = 0; i < 10; i++) {
int size = buckets.get(i).size();
for (int ii = 0; ii < size; ii++) {
nums[nn++] = buckets.get(i).get(ii);
}
buckets.get(i).clear();
}
location++;
}
}
}
Performance analysis of Radix sorting
- Time complexity
Time complexity O(n+k), where n is the number of array elements, and K is the highest number of array elements.
- Spatial complexity
Like bucket sorting, because the storage space of bucket is introduced, the space complexity is O(n+k).
- stability
In the cardinality sorting process, the elements with the same value as the current digit are uniformly allocated to the bucket each time, and the positions are not exchanged, so the cardinality sorting is stable.
summary
In this article, we have learned ten basic sorting to briefly summarize.
First, the simplest bubble sorting: two-layer circulation, adjacent exchange;
Select sort: unsorted and sorted. Find the smallest element in the unsorted sequence and put it at the end of the sorted sequence;
Insertion sort: the landlords touch the card thinking, and insert an element into the appropriate position of the ordered sequence;
Hill sort: insert sort plus, first divide the sequence, and then insert sorting respectively;
Merge sort: the first bullet of divide and conquer idea is to cut the sequence first, and then sort in the merging process;
Quick sort: the second bullet of divide and conquer idea, the benchmark number partitions the original sequence, the small one on the left and the large one on the right;
Heap sort: select sort plus, create a large top heap, insert the top element (maximum value) into the end of the sequence, and then float the new element.
Counting and sorting: the first bullet of space for time, count the occurrence times of corresponding elements by using the new array, output the subscript of the new array, and sort the original array;
Bucket sorting: the second bullet of space for time, divide the elements of the original array into several buckets, sort each bucket separately, and then spell the elements in the bucket;
Cardinality sorting: the third bullet of space for time, bucket sorting plus, divide the elements into buckets according to the digits, and then compare them according to each digit.
Summary of top ten basic sorting performance:
| Sorting method | Time complexity (average) | Time complexity (worst case) | Time complexity (best) | Spatial complexity | stability |
|---|---|---|---|---|---|
| Bubble sorting | O(n²) | O(n²) | O(n) | O(1) | stable |
| Select sort | O(n²) | O(n²) | O(n²) | O(1) | instable |
| Insert sort | O(n²) | O(n²) | O(n) | O(1) | stable |
| Shell Sort | O(n^(1.3-2)) | O(n²) | O(n) | O(1) | instable |
| Merge sort | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | stable |
| Quick sort | O(nlogn) | O(n²) | O(nlogn) | O(nlogn) | instable |
| Heap sort | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | instable |
| Count sort | O(n+k) | O(n+k) | O(n+k) | O(n) | stable |
| Bucket sorting | O(n+k) | O(n²) | O(n) | O(n+k) | stable |
| Cardinality sort | O(n*k) | O(n*k) | O(n*k) | O(n+k) | stable |
Do simple things repeatedly, do repeated things seriously, and do serious things creatively.
I am three evil, a full stack development capable of writing and martial arts.
Praise, pay attention and don't get lost. I'll see you next time!
reference resources:
[1].This is perhaps the best article to analyze the top ten sorting algorithms in the eastern hemisphere
[2]. https://github.com/chefyuan/algorithm-base
[2]. Data structure and algorithm analysis
[3]. Interview frequency: the eight commonly used sorting algorithms in Java are caught in a net!
[4]. Ten classical sorting algorithms (dynamic graph demonstration)
[5]. Analyzing arrays. In JDK8 The underlying principle of sort and the selection of sorting algorithm