summary
List, set and Map are all interfaces. The first two are inherited from the Collection interface, and Map is an independent interface
There are ArrayList, Vector and LinkedList under List
Under Set, there are HashSet, LinkedHashSet and TreeSet
There are Hashtable, LinkedHashMap, HashMap and TreeMap under the Map
There is also a Queue interface under the Collection interface, with the PriorityQueue class
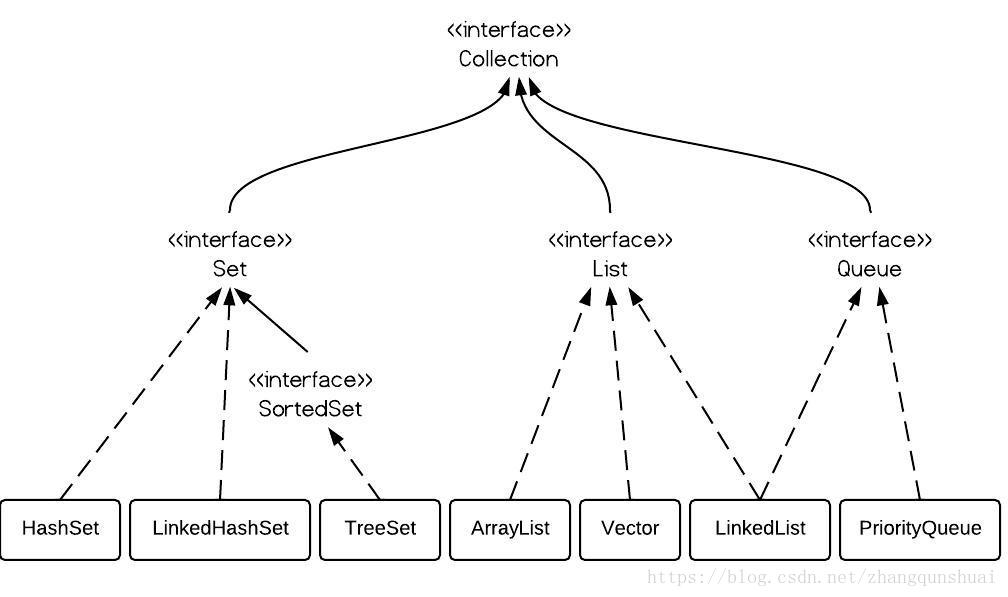
The Queue interface is at the same level as List and Set, and both inherit the Collection interface. Looking at the figure, you will find that LinkedList can implement both Queue interface and List interface. However, LinkedList implements the Queue interface. The Queue interface narrows the access rights to LinkedList methods (that is, if the parameter type in the method is Queue, it can only access the methods defined by the Queue interface, but not the non Queue methods of LinkedList directly), so that only appropriate methods can be used.
SortedSet is an interface, and the elements in it (only the implementation of TreeSet is available) must be ordered.
Collection interface
List: ordered and repeatable
ArraysList
Advantages: the underlying data structure is array, fast query and slow addition and deletion.
Disadvantages: unsafe thread and high efficiency
Vector
Advantages: the underlying data structure is array, fast query and slow addition and deletion.
Disadvantages: thread safety and low efficiency
LinkedList
Advantages: the underlying data structure is linked list, with slow query and fast addition and deletion.
Disadvantages: unsafe thread and high efficiency
Set: unordered, unique
HashSet
The underlying data structure is a hash table. (unordered, unique)
How to ensure element uniqueness?
Rely on two methods: hashCode() and equals()
LinkedHashSet
The underlying data structure is linked list and hash table. (FIFO insertion is orderly and unique)
1. Ensure element order by linked list
2. The hash table ensures the uniqueness of elements
Tree Set
The underlying data structure is a red black tree. (orderly, unique)
1. How to ensure element sorting? Natural sorting and comparator sorting
2. How to ensure the uniqueness of elements? It is determined according to whether the return value of the comparison is 0
Map interface
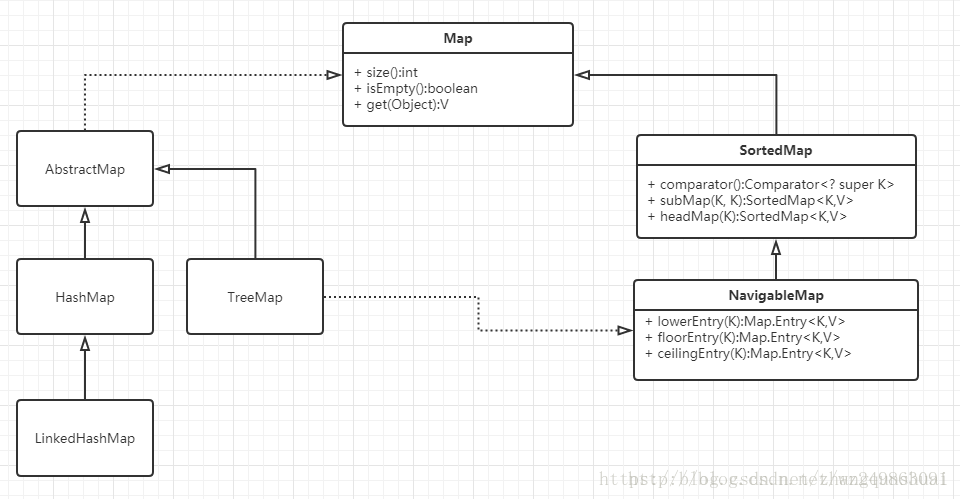
Map interface has three important implementation classes, namely HashMap, TreeMap and HashTable.
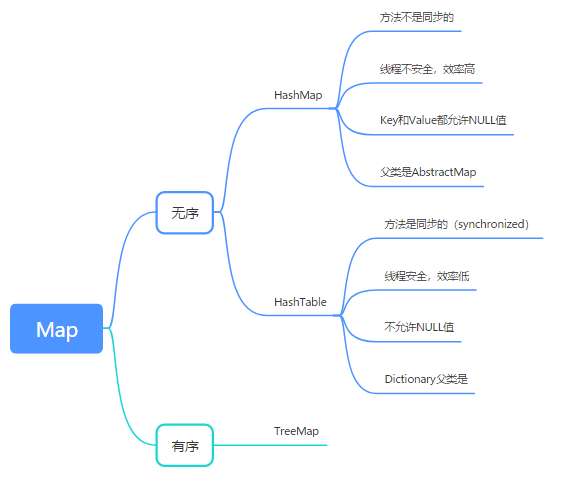
- HashMap and HashTable are disordered, and TreeMap is ordered
- The Hashtable method is synchronous, but the HashMap method is not synchronous. This is the main difference between the two.
This means:
- Hashtable is thread safe, and HashMap is not thread safe.
- Hashtable is less efficient and HashMap is more efficient.
- If there are no requirements for synchronization or compatibility with legacy code, HashMap is recommended.
- Looking at the source code of Hashtable, you can find that except for the constructor, all public method declarations of Hashtable have the synchronized keyword, while the source code of HashMap does not.
- Hashtable does not allow null values, and HashMap allows null values (both key and value are allowed)
- The parent class is different: the parent class of Hashtable is Dictionary, and the parent class of HashMap is AbstractMap
The difference between TreeSet, HashSet and linkedhashset
1. Introduction
TreeSet, LinkedHashSet and HashSet are data structures that implement Set in java
- The main function of TreeSet is to sort
- The main function of LinkedHashSet is to ensure that FIFO is an ordered set (first in first out)
- HashSet is just a general collection of stored data
2. Similarities
- Duplicates elements: because all three implement Set interface, they do not contain the same elements
- Thread safety: none of the three is thread safe. If you want to use thread safety, you can use collections synchronizedSet()
3. Differences
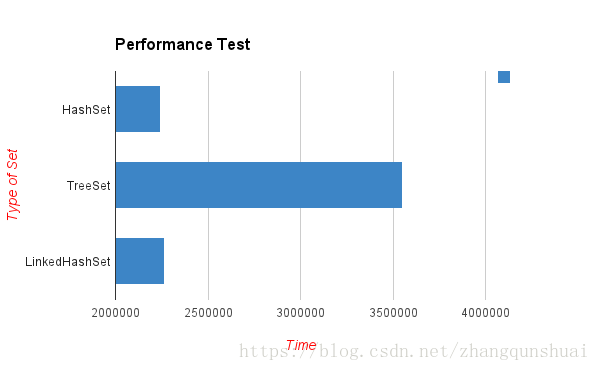
- Performance and Speed: HashSet is the fastest to insert data, followed by LinkHashSet, and TreeSet is the slowest because sorting is implemented internally
- Ordering: HashSet does not guarantee order. LinkHashSet guarantees that FIFO is sorted according to the insertion order. TreeSet can implement sorting internally or customize the sorting rules
- Null: null data is allowed in HashSet and LinkHashSet, but NullPointerException will be reported when null data is inserted in TreeSet
4. Code comparison
public static void main(String args[]) {
HashSet<String> hashSet = new HashSet<>();
LinkedHashSet<String> linkedHashSet = new LinkedHashSet<>();
TreeSet<String> treeSet = new TreeSet<>();
for (String data : Arrays.asList("B", "E", "D", "C", "A")) {
hashSet.add(data);
linkedHashSet.add(data);
treeSet.add(data);
}
//Order is not guaranteed
System.out.println("Ordering in HashSet :" + hashSet);
//FIFO ensures the order of installation and insertion
System.out.println("Order of element in LinkedHashSet :" + linkedHashSet);
//Internal implementation sorting
System.out.println("Order of objects in TreeSet :" + treeSet);
}
Operation results: Ordering in HashSet :[A, B, C, D, E] (lack order) Order of element in LinkedHashSet :[B, E, D, C, A] (FIFO Insert order) Order of objects in TreeSet :[A, B, C, D, E] (sort)
Comparison of two sorting methods of TreeSet
1. Introduction of sorting (taking sorting of basic data types as an example)
Because TreeSet can sort elements according to certain rules, for example, the following example
public class MyClass {
public static void main(String[] args) {
// Object collection creation
// Sort in natural order
TreeSet<Integer> ts = new TreeSet<Integer>();
// Create elements and add
// 20,18,23,22,17,24,19,18,24
ts.add(20);
ts.add(18);
ts.add(23);
ts.add(22);
ts.add(17);
ts.add(24);
ts.add(19);
ts.add(18);
ts.add(24);
// ergodic
for (Integer i : ts) {
System.out.println(i);
}
}
}
Operation results: 17 18 19 20 22 23 24
2. If it is a reference data type, such as a user-defined object, how to sort it?
public class MyClass {
public static void main(String[] args) {
TreeSet<Student> ts=new TreeSet<Student>();
//Create element object
Student s1=new Student("zhangsan",20);
Student s2=new Student("lis",22);
Student s3=new Student("wangwu",24);
Student s4=new Student("chenliu",26);
Student s5=new Student("zhangsan",22);
Student s6=new Student("qianqi",24);
//Adds an element object to a collection object
ts.add(s1);
ts.add(s2);
ts.add(s3);
ts.add(s4);
ts.add(s5);
ts.add(s6);
//ergodic
for(Student s:ts){
System.out.println(s.getName()+"-----------"+s.getAge());
}
}
}
public class Student {
private String name;
private int age;
public Student() {
super();
// TODO Auto-generated constructor stub
}
public Student(String name, int age) {
super();
this.name = name;
this.age = age;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
}
Cause analysis:
Because I don't know which sort method to follow, an error will be reported.
resolvent:
1. Natural sorting
2. Comparator sorting
(1). Natural sorting
Natural sorting requires the following operations:
1. Implement the Comparable interface in the student class
2. Rewrite the Compareto method in the Comparable interface
compareTo(T o) Compares the order of this object with the specified object.
public class Student implements Comparable<Student>{
private String name;
private int age;
public Student() {
super();
// TODO Auto-generated constructor stub
}
public Student(String name, int age) {
super();
this.name = name;
this.age = age;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
@Override
public int compareTo(Student s) {
//return -1; //-1 means to put it on the left of the red black tree, that is, output in reverse order
//return 1; //1 indicates that it is placed on the right side of the red black tree, that is, sequential output
//return o; // Indicates that the elements are the same, and only the first element is stored
//The main condition is the length of the name. If the length of the name is small, it will be placed in the left subtree, otherwise it will be placed in the right subtree
int num=this.name.length()-s.name.length();
//The same length of the name does not mean the same content. If this String object precedes the parameter String in dictionary order, the comparison result is a negative integer.
//If this String object follows the parameter String in dictionary order, the comparison result is a positive integer.
//If the two strings are equal, the result is 0
int num1=num==0?this.name.compareTo(s.name):num;
//The same length and content of the name does not mean the same age, so we should judge the age
int num2=num1==0?this.age-s.age:num1;
return num2;
}
}
Operation results:
lis-----------22 qianqi-----------24 wangwu-----------24 chenliu-----------26 zhangsan-----------20 zhangsan-----------22
(2). Comparator sort
Comparator sorting steps:
1. Create a comparison class separately. Take MyComparator as an example and let it inherit the Comparator interface
2. Rewrite the Compare method in the Comparator interface
compare(T o1,T o2) Compare the two parameters used to sort.
3. Use the following construction method in the main class
TreeSet(Comparator<? superE> comparator) //Construct a new empty TreeSet that sorts according to the specified comparator.
public class MyClass {
public static void main(String[] args) {
//Object collection creation
//TreeSet (comparator <? Super E > comparator) constructs a new empty TreeSet, which sorts according to the specified comparator.
TreeSet<Student> ts=new TreeSet<Student>(new MyComparator());
//Create element object
Student s1=new Student("zhangsan",20);
Student s2=new Student("lis",22);
Student s3=new Student("wangwu",24);
Student s4=new Student("chenliu",26);
Student s5=new Student("zhangsan",22);
Student s6=new Student("qianqi",24);
//Adds an element object to a collection object
ts.add(s1);
ts.add(s2);
ts.add(s3);
ts.add(s4);
ts.add(s5);
ts.add(s6);
//ergodic
for(Student s:ts){
System.out.println(s.getName()+"-----------"+s.getAge());
}
}
}
public class Student {
private String name;
private int age;
public Student() {
super();
// TODO Auto-generated constructor stub
}
public Student(String name, int age) {
super();
this.name = name;
this.age = age;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
}
public class MyComparator implements Comparator<Student> {
@Override
public int compare(Student s1,Student s2) {
// Name length
int num = s1.getName().length() - s2.getName().length();
// Name content
int num2 = num == 0 ? s1.getName().compareTo(s2.getName()) : num;
// Age
int num3 = num2 == 0 ? s1.getAge() - s2.getAge() : num2;
return num3;
}
}
Operation results:
lis-----------22 qianqi-----------24 wangwu-----------24 chenliu-----------26 zhangsan-----------20 zhangsan-----------22
(3) Performance test
class Dog implements Comparable<Dog> {
int size;
public Dog(int s) {
size = s;
}
public String toString() {
return size + "";
}
@Override
public int compareTo(Dog o) {
//Value size comparison
return size - o.size;
}
}
public class MyClass {
public static void main(String[] args) {
Random r = new Random();
HashSet<Dog> hashSet = new HashSet<Dog>();
TreeSet<Dog> treeSet = new TreeSet<Dog>();
LinkedHashSet<Dog> linkedSet = new LinkedHashSet<Dog>();
// start time
long startTime = System.nanoTime();
for (int i = 0; i < 1000; i++) {
int x = r.nextInt(1000 - 10) + 10;
hashSet.add(new Dog(x));
}
// end time
long endTime = System.nanoTime();
long duration = endTime - startTime;
System.out.println("HashSet: " + duration);
// start time
startTime = System.nanoTime();
for (int i = 0; i < 1000; i++) {
int x = r.nextInt(1000 - 10) + 10;
treeSet.add(new Dog(x));
}
// end time
endTime = System.nanoTime();
duration = endTime - startTime;
System.out.println("TreeSet: " + duration);
// start time
startTime = System.nanoTime();
for (int i = 0; i < 1000; i++) {
int x = r.nextInt(1000 - 10) + 10;
linkedSet.add(new Dog(x));
}
// end time
endTime = System.nanoTime();
duration = endTime - startTime;
System.out.println("LinkedHashSet: " + duration);
}
}
Default size and capacity expansion mechanism of common Java collections
During the background development of the interview, the collection is a hot topic in the interview. We should not only know the different usage of each collection, but also know the capacity expansion mechanism of the collection. Today, let's talk about the default size and capacity expansion mechanism of ArrayList and HashMap.
In Java 8, you can see from the source code: the default size of ArrayList is 10 elements, and the default size of HashMap is 16 elements (it must be a power of 2, why??? It is explained below). This is the code fragment of ArrayList and HashMap classes in Java 8:
// from ArrayList.java JDK 1.7 private static final int DEFAULT_CAPACITY = 10; //from HashMap.java JDK 7 static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
The reasons for these commonly used default initial capacity and expansion are as follows:
When the underlying implementation involves capacity expansion, the container needs to reallocate a larger continuous memory (if it is a discrete allocation, it does not need to reallocate. The discrete allocation is to dynamically allocate memory when new elements are inserted). It is necessary to copy all the original data of the container to the new memory, which undoubtedly greatly reduces the efficiency. The coefficient of loading factor is less than or equal to 1, which means that when the number of elements exceeds the coefficient of capacity length * loading factor, capacity expansion is carried out. In addition, the capacity expansion also has a default multiple, and the capacity expansion of different containers is different.
List: elements are ordered and repeatable
The default initial capacity of ArrayList and Vector is 10
Vector: thread safe, slow, capacity expansion 10 – > 20
The underlying data structure is an array structure
The loading factor is 1: that is, when the number of elements exceeds the capacity length, the capacity will be expanded
Capacity expansion increment: 1 time of the original capacity
If the capacity of Vector is 10, the capacity after one expansion is 20
ArrayList: thread unsafe, fast, capacity expansion 10 – > 16
The underlying data structure is an array structure
Capacity expansion increment: 0.5 times of the original capacity + 1
For example, the capacity of ArrayList is 10, and the capacity after one expansion is 16
Set: elements are out of order and cannot be repeated
HashSet: thread unsafe, fast access speed, capacity expansion 16 – > 32
The underlying implementation is a HashMap (save data), which implements the Set interface
The default initial capacity is 16 (see the description of HashMap below for why it is 16)
The loading factor is 0.75: that is, when the number of elements exceeds 0.75 times the capacity length, the capacity will be expanded
Capacity expansion increment: 1 time of the original capacity
For example, the capacity of HashSet is 16, and the capacity after one expansion is 32
Map: two column set
HashMap: the default initial capacity is 16 and the one-time expansion capacity is 32
(why 16:16 is 2 ^ 4, which can improve the query efficiency. In addition, 32 = 16 < < 1)
The loading factor is 0.75: that is, when the number of elements exceeds 0.75 times the capacity length, the capacity will be expanded
Capacity expansion increment: 1 time of the original capacity
For example, the capacity of HashSet is 16, and the capacity after one expansion is 32
Why is the length of HashMap array to the power of 2?
The array length of hashMap must maintain the power of 2. For example, if the binary representation of 16 is 10000, then the length-1 is 15 and the binary representation is 01111. Similarly, the array length after capacity expansion is 32, the binary representation is 100000, the length-1 is 31 and the binary representation is 01111.
This will ensure that all the low bits are 1, and there is only one bit difference after capacity expansion, that is, there is an extra 1 in the leftmost bit. In this way, when passing through H & (length-1), as long as the leftmost difference corresponding to h is 0, it can ensure that the new array index is consistent with the old array index (greatly reducing the data position re exchange of the old array with good hashing). In addition, The array length is kept to the power of 2, and the low order of length-1 is 1, which will make the obtained array index more uniform.
static int indexFor(int h, int length) {
return h & (length-1);
}
First, calculate the hashcode value of the key, and then perform an and operation (&) with the length of the array - 1. It looks very simple, but in fact it has a mystery. For ex amp le, if the length of the array is the fourth power of 2, hashcode will do an "and" operation with the fourth power of 2 - 1.
Why is HashMap most efficient when its array initialization is to the power of 2?
Many people have this question. Why is hashmap the most efficient when the array initialization size of hashmap is the power of 2? Let me take the power of 2 as an example to explain why hashmap has the highest access performance when the array size is the power of 2.
Look at the figure below. The two groups on the left have an array length of 16 (the fourth power of 2), and the two groups on the right have an array length of 15. The hashcode s of the two groups are 8 and 9, but obviously, when they are "and" with 1110, they produce the same result, that is, they will be located at the same position in the array, which leads to collision. 8 and 9 will be placed on the same linked list, so it is necessary to traverse the linked list to get 8 or 9 during query, which reduces the efficiency of query.
At the same time, we can also find that when the array length is 15, the value of hashcode will be "and" with 14 (1110), so the last bit will always be 0, and 00010011011001101111101 can never store elements, which wastes a lot of space. What's worse, in this case, The position where the array can be used is much smaller than the length of the array, which means that it further increases the probability of collision and slows down the efficiency of query!
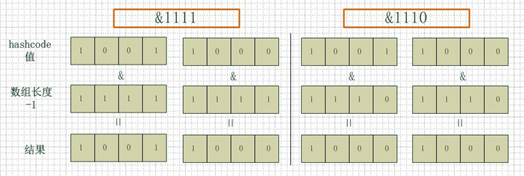
Therefore, when the array length is the n-th power of 2, the probability of the same index calculated by different key s is small, so the data is evenly distributed on the array, that is, the probability of collision is small. In contrast, when querying, you don't have to traverse the chain table at a certain position, so the query efficiency is higher.
At this point, let's look back at the default array size in hashmap. Looking at the source code, we can see that it is 16. Why is it 16 instead of 15 or 20? After seeing the above explanation, we will be clear. Obviously, it is because 16 is an integer power of 2,
In the case of small amount of data, 16 can reduce the collision between key s and speed up the efficiency of query than 15 and 20.