In deep learning, we often need to do four rules, linear transformation and activation of tensors.
1. Function operation of single tensor
t = torch.rand(2, 2) # Generate a 3x3 tensor print(t) print(t.sqrt()) # Square root of tensor, tensor internal method print(torch.sqrt(t)) # Square root of tensor, functional form print(t.sqrt_()) # Square root in place operation print(torch.sum(t)) # Sum all elements print(torch.sum(t, 0)) # Summation of elements in the 0th dimension print(torch.sum(t, [0, 1])) # Sum 0,1-dimensional elements print(torch.mean(t, [0, 1])) # Averaging 0,1-dimensional elements

2. Function operation of multiple tensors
In pytorch, the operators of addition, subtraction, multiplication and division can be used for the operation between tensors, and the methods of add, sub, mul and div can also be used for the operation.
t1 = torch.rand(2, 2)
t2 = torch.rand(2, 2)
# Element addition
print(t1.add(t2))
print(t1+t2)
print('=' * 50)
# Element subtraction
print(t1.sub(t2))
print(t1-t2)
print('=' * 50)
# Element multiplication
print(t1.mul(t2))
print(t1*t2)
print('=' * 50)
# Element division
print(t1.div(t2))
print(t1/t2)
print('=' * 50)

3. Extremum and ordering of tensors
t = torch.randn(3, 3)
print(t)
print('=' * 50)
print(torch.max(t, 0)) # Maximum value along dimension 0
print(torch.argmax(t, 0)) # The maximum value of the index position 0 along the dimension
print('=' * 50)
print(torch.min(t, 0)) # Minimum value along dimension 0
print(torch.argmin(t, 0)) # Minimum index position along dimension 0
print('=' * 50)
print(t.sort(-1)) # Sorting along the last dimension returns the sorted tensor and the original position of tensor elements in the changed dimension

4. Multiplication of matrix and contraction and union of tensor
4.1 matrix multiplication of pytorch tensor
torch can be used for Matrix Multiplication Mm (mm stands for Matrix Multiplication). You can also use the built-in MM method for Matrix Multiplication, or use the @ operator.
t1 = torch.randn(3, 4) # Establish a 3x4 tensor
t2 = torch.randn(4, 3) # Establish a 4x3 tensor
# Matrix multiplication
print(torch.mm(t1, t2)) # Matrix multiplication
print(t1.mm(t2))
print(t1@t2)
print('=' * 50)
a1 = torch.randn(2, 3, 4)
a2 = torch.randn(2, 4, 3)
print(torch.bmm(a1, a2)) # (mini) batch matrix multiplication, and the return result is 2x3x3
print(a1.bmm(a2))
print(a1@a2)

4.2 torch. Use of einsum function
When calculating the product of larger dimensions, it is usually necessary to determine which dimensions the multiplication results of respective tensor elements are summed. This operation is called contraction and requires the introduction of Einstein summation convention.
c
i
j
k
a
b
c
=
∑
l
1
l
2
.
.
.
l
n
=
A
i
j
k
.
.
.
m
l
1
l
2
.
.
.
l
n
B
a
b
c
.
.
.
m
l
1
l
2
.
.
.
l
n
c_{ijkabc}=\sum_{l_1l_2...l_n}=A_{ijk...ml_1l_2...l_n}B_{abc...ml_1l_2...l_n}
cijkabc=l1l2...ln∑=Aijk...ml1l2...lnBabc...ml1l2...ln
Among them, there are two tensors involved in the operation, which are recorded as A and B respectively, and the output result is C. here, the corresponding dimensional subscripts are divided into three categories: they appear in A, B and C, which means that A series of elements corresponding to the two subscripts do pairwise product (i.e. tensor product); If it appears in A and B but not in C, it means that some column elements corresponding to two subscripts are summed by product (similar to inner product); It appears in A and B and only once in C, and the dimensions corresponding to these two indicators are the same, which means that the two dimensions are multiplied by position.
t1 = torch.randn(2, 3, 4)
t2 = torch.randn(2, 4, 3)
print(t1.bmm(t2)) # Results of batch matrix multiplication
print('=' * 50)
print(torch.einsum('bnk,bkl -> bnl', t1, t2)) # einsum calculation

torch. When using the einsum function, you need to pass in the shape corresponding to the subscript of the two tensors, distinguish them with different letters (the letters can be selected arbitrarily, just obey the previous rules), and the final shape, connect them with the - > symbol, and finally pass in the two input tensors to get the output result. It should be noted that the dimension of the summation indicator must be the same, otherwise an error will be reported.
5. Splicing and segmentation of tensors
t1 = torch.randn(3, 4)
t2 = torch.randn(3, 4)
t3 = torch.randn(3, 4)
print(torch.stack([t1,t2,t3], -1).shape) #Stack along the last dimension and return a tensor with a size of 3x4x3
print('=' * 50)
t = torch.randn(3, 6)
print(t.split([1,2,3], -1)) # The tensor is divided into three tensors along the last dimension
print('=' * 50)
print(t.split(3, -1)) # Zhang Liang is divided along the last dimension, the segmentation size is 3, and the output tensor size is 3x2
print('=' * 50)
print(t.chunk(3, -1)) # Zhang Liang is divided along the last dimension, the segmentation size is 3, and the output tensor size is 3x2

6. Expansion and compression of tensor dimension
t = torch.rand(3, 4)
print(t.shape)
print(t.unsqueeze(-1).shape) # Amplify the last dimension
print(t.unsqueeze(-1).unsqueeze(-1).shape) # Continue to expand the last dimension
print('=' * 50)
t2 = torch.rand(1,3,4,1)
print(t.shape)
print(t.squeeze().shape) # Compress all dimensions of size 1
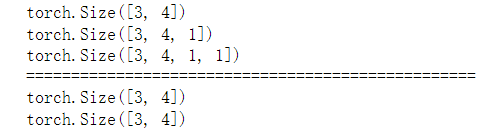
7. Tensor broadcasting
Suppose that the size of one tensor is 3x4x5 and the size of the other tensor is 3x5. In order to allow the two tensors to perform four operations, it is necessary to expand the shape of the second tensor into 3x1x5, so that the two tensors can control it. When two tensors are calculated, the 3x1x5 tensor will be copied four times along the second dimension to become a 3x4x5 tensor, so that the two tensors can be calculated.
t1 = torch.randn(3,4,5) t2 = torch.randn(3,5) t2 = t2.unsqueeze(1) # Change the shape of the tensor to 3x1x5 t3 = t1 + t2 # Broadcast summation, the final result is 3x4x5 tensor print(t3) print(t3.shape)