Catalog
G:POJ-2752 Seek the Name, Seek the Fame
Explanation of Algorithms KMP algorithm in detail)
It took a long time to understand that the most important thing for KMP is the understanding of next array. You can watch the video first. KMP algorithm video.
KMP algorithm is one of the most well-known algorithms that should be talked about in every book of Data Structure, but unfortunately, I didn't understand it at all in my sophomore year.~~~
After that, I often see articles explaining KMP algorithm in many places. After reading for a long time, I seem to know what is going on, but I always feel that there are some places I still do not fully understand. These two days spent a little time to sum up, a little experience, I hope I can use my own language to sort out some details of this algorithm, it is also a test that I really understand this algorithm.
What is KMP algorithm?
KMP was discovered by three bulls: D.E.Knuth, J.H.Morris and V.R.Pratt. The first one is the author of Art of Computer Programming!!
The problem to be solved by KMP algorithm is the pattern location problem in the string (also known as the main string). To put it simply, we usually say keyword search. A pattern string is a keyword (next called P), and if it appears in a main string (next called T), it returns to its specific location or - 1 (commonly used means).
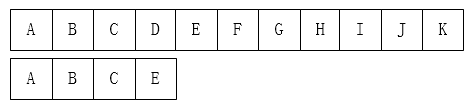
First of all, there is a very simple idea for this problem: matching from left to right, if there is a character mismatch in the process, jump back and move the pattern string one bit to the right. What's the difficulty?
We can initialize it like this:
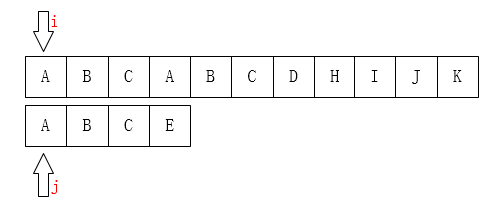
Then we just need to compare whether the character pointed by the i pointer is the same as the character pointed by the j pointer. If they are consistent, they all move backwards. If they are not, the following is the picture:
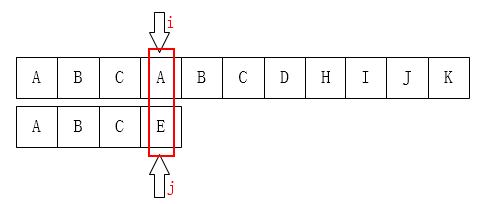
If A and E are not equal, then move the i pointer back to the first place (assuming the subscript starts at 0), j to the zero place of the pattern string, and then start the step again:
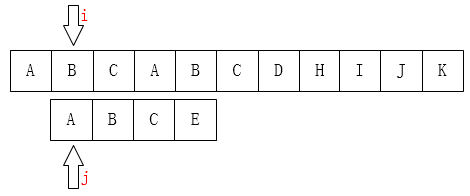
Based on this idea, we can get the following procedures:
/**
* brute-force attack
* @param ts Main string
* @param ps Pattern string
* @return If found, return the subscript of the first character in the main string, otherwise - 1
*/
public static int bf(String ts, String ps) {
char[] t = ts.toCharArray();
char[] p = ps.toCharArray();
int i = 0; // Location of main string
int j = 0; // Location of pattern strings
while (i < t.length && j < p.length) {
if (t[i] == p[j]) { // When two characters are the same, compare the next
i++;
j++;
} else {
i = i - j + 1; // Once the mismatch occurs, i falls back
j = 0; // j return to 0
}
}
if (j == p.length) {
return i - j;
} else {
return -1;
}
}The above program is no problem, but not good enough! (Think of a sentence from my high school digital teacher: I can't say you're wrong, I can only say you're wrong ~)
If we are looking for it artificially, we will certainly not move i back to the first place, because there is no A in front of the failed matching position of the main string except the first A. Why can we know that there is only one A in front of the main string? Because we already know that the first three characters match! This is very important. Moving past certainly does not match! There's an idea that i can stay still, we just need to move j, as follows:
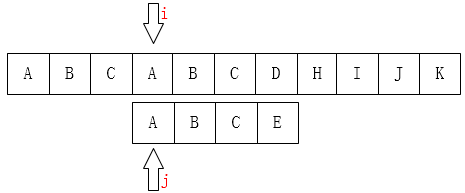
The above situation is still ideal, and we will compare it again at most. But if we look for "SS SSSSB" in the main string "SSSSSSSSSSSA", we will not know the mismatch until the last one, and then i traceback, this efficiency is obviously the lowest.
Daniels can't stand the inefficient means of "violent cracking", so they three developed KMP algorithm. The idea is just like what we saw above: "Using the valid information that has been partially matched, keep the i pointer from backtracking, and by modifying the j pointer, let the pattern string move to the valid position as far as possible."
So the whole point of KMP is that when a character does not match the main string, we should know where the j pointer is going to move.
Next, let's discover the law of j's movement by ourselves:
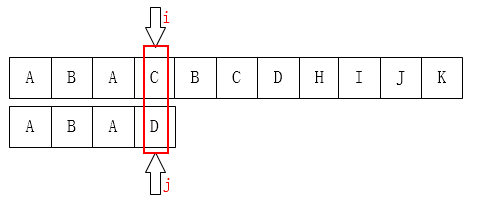
Figure: C and D don't match. Where do we move j? Apparently number one. Why? Because there is an A in front of it.
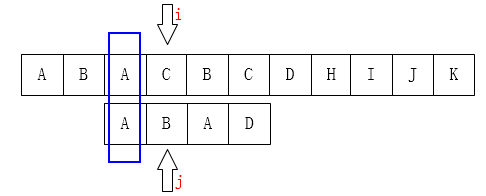
The same is true of the following figures:
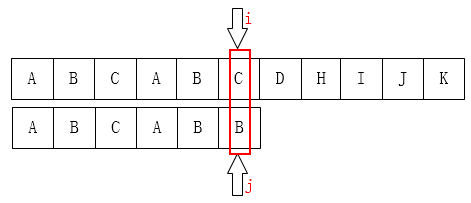
You can move the j pointer to the second place because the first two letters are the same:
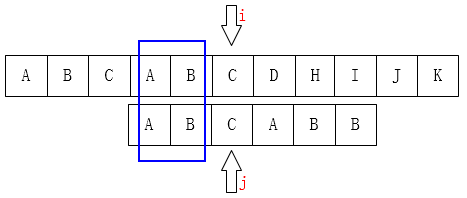
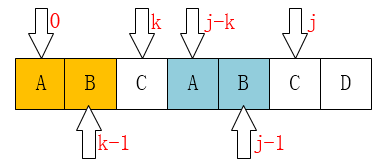
At this point, we can probably see a little bit of the end, when the match fails, j will move to the next position K. There is a property that the first k characters are the same as the last K characters before j.
If this is expressed in mathematical formulas
P[0 ~ k-1] == P[j-k ~ j-1]
This is quite important. If you find it difficult to remember, you can understand it by the following figure:
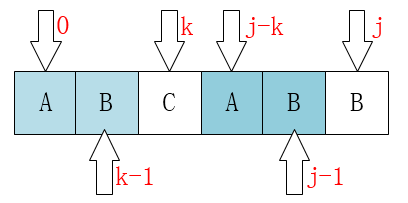
Understanding this should make it possible to understand why j can be moved directly to k.
Because:
When T[i]!= P[j]
There is T [i-j ~ i-1]== P [0 ~ j-1]
By P [0~k-1]=== P [j-k~j-1]
Necessity: T [i-k~i-1]== P [0~k-1]
The formula is boring. You can see it clearly. You don't need to remember it.
This paragraph is just to prove why we can move j directly to k without comparing the previous k characters.
Okay, so here's the point. How do I get this k? Because every position of P may mismatch, that is to say, we need to calculate the K corresponding to each position j, so we use an array next to save, next[j] = k, which means the next position of J pointer when T [i]!= P [j].
Many textbooks or blog posts in this place are vague or simply passed through, or even paste a piece of code, why is this? How can we do this? It's not clear at all. And this is the most critical part of the whole algorithm.
public static int[] getNext(String ps) {
char[] p = ps.toCharArray();
int[] next = new int[p.length];
next[0] = -1;
int j = 0;
int k = -1;
while (j < p.length - 1) {
if (k == -1 || p[j] == p[k]) {
next[++j] = ++k;
} else {
k = next[k];
}
}
return next;
}This version of the next array algorithm should be the most widely circulated, the code is very concise. But it's really hard to understand. What's the basis of this calculation?
Okay, let's put this aside and deduce the idea ourselves. Now let's always remember that the value of next[j] (i.e. k) represents the next move of the j pointer when P [j]!= T [i].
Let's start with the first one: When j is 0, what if it doesn't match?
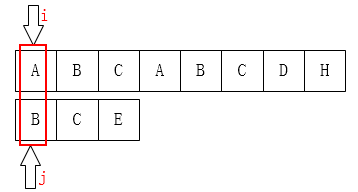
As shown above, j is already on the far left and can't move any more. It's time to move the i pointer backwards. So there's next [0]= - 1 in the code; this initialization.
What if j is 1?
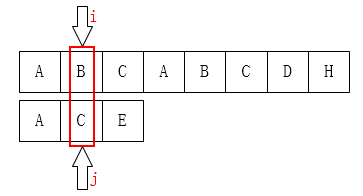
Obviously, the j pointer must be moved back to zero. Because that's the only place in front of it.~~~
The following is the most important one. See the following picture:
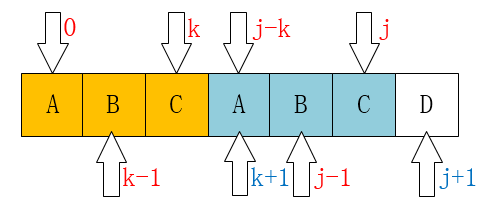
Please compare these two pictures carefully.
We find a rule:
When P [k]== P [j],
There is next [j + 1]== next [j] + 1
In fact, this can be proved:
Because before P[j], P [0-k-1]== P[j-k-j-1]. (next [j]== k)
At this time, the existing P [k]= P [j], can we get P [0 ~ k-1] + P [k]== P [j-k ~ j-1] + P [j].
That is, P [0-k]== P [j-k-j], that is, next [j+1]== k+1== next [j]+1.
The formula here is not very easy to understand, or it will be easier to understand by looking at the pictures.
What if P [k]!= P [j]? For example, the following figure shows:
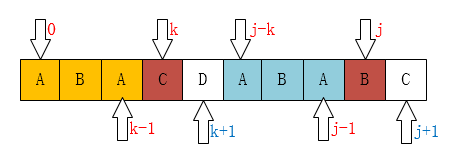
In this case, if you look at the code, it should be this sentence: k = next[k]; why? You should see below.
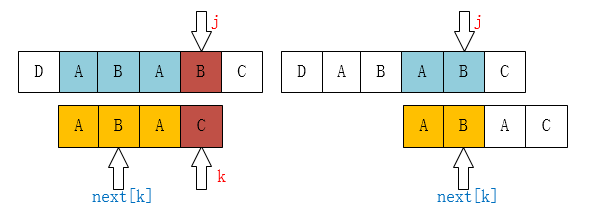
Now you should know why k = next[k]! Like the example above, we can't find the longest suffix string [A, B, A, B], but we can still find prefix string [A, B], [B]. So this process is not like locating the string [A, B, A, C]. When C is different from the main string (that is, K is different), of course, it moves the pointer to next[k].
With the next array, everything will be fine. We can write the KMP algorithm by hand.
public static int KMP(String ts, String ps) {
char[] t = ts.toCharArray();
char[] p = ps.toCharArray();
int i = 0; // Location of main string
int j = 0; // Location of pattern strings
int[] next = getNext(ps);
while (i < t.length && j < p.length) {
if (j == -1 || t[i] == p[j]) { // When j is - 1, the move is i, and of course j is 0.
i++;
j++;
} else {
// i don't need to go back.
// i = i - j + 1;
j = next[j]; // j goes back to the specified location
}
}
if (j == p.length) {
return i - j;
} else {
return -1;
}
}Compared with violent cracking, it has changed four places. One of the most important points is that i doesn't need to go back.
NEXT Array Explanation NEXT Array Explanation)
The next array method of KMP is not easy to understand, but also the most important part. I will use my own perception to deduce this article slowly. Make sure you know what you see and why.
If you don't know what KMP is, please read the link above and understand what KMP is about.
Now let's talk about the next array method of KMP.
The next array of KMP is simple, assuming that there are two strings, one is the strText to be matched, and the other is the keyword strKey to be looked up. Now let's look in strText to see if it contains strKey, which character strText traverses with i, and which character strKey matches with j.
If it is a violent search method, when strText[i] and strKey[j] fail to match, I and j all go back, and then start to re-match from the next character of i-j.
KMP ensures that i never goes back, and only j goes back to improve the matching efficiency. It uses strKey's mismatched J as a feature of previously successfully matched substrings to find where j should fall back. This substring is characterized by the same degree of prefix and suffix.
So the next array is actually to find out how many bits of the prefix and suffix of each preceding substring in strKey match, so as to determine where to go back when j mismatch occurs.
I know the above nonsense is hard to understand. Let's take a look at a color picture below.

The picture is strKey, the keyword string to be looked up. Suppose we have an empty next array, our job is to fill in the next array.
Next, we use mathematical induction to solve the problem of filling in values.
Here we draw on the three steps of mathematical induction (or dynamic programming?) :
1. Initial state
2. Let's assume that we have finished filling in the jth place and before the jth place.
3. How to Fill in Inference No. j+1
Let's talk about the initial state later. Let's just assume that we've filled it out before and after the jth position. That is to say, from the above figure, we have the following known conditions:
next[j] == k;
next[k]= = the index where the green color block is located;
next [index of green color block] = index of yellow color block;
Here's a note: The color blocks on the map are the same size (don't lie to me? Well, ignore the size of the color block, which represents only one of the arrays.
Let's look at the following chart for more information:

1. Under the condition of "next [j]= k;", we can get A1 substring== A2 substring (according to the definition of next array, prefix and suffix that).
2. By "next[k]= the index of the green color block;" under this condition, we can get B1 substring== B2 substring.
3. Under the condition of "next [index of green color block]== index of yellow color block"; we can get C1 substring== C2 substring.
4. From 1 and 2 (A1 = A2, B1 = B2), we can get B1 = B2 = B3.
5. From 2 and 3 (B1 = B2, C1 = C2), C1 = C2 = C3 can be obtained.
6.B2 = B3 yields C3 = C4 = C1 = C2
The above one is very simple geometric mathematics, you can read it carefully. Here I use the same color line segments to represent exactly the same subarray for easy observation.
Next, we begin to use the above conditions to derive how much we should fill in next[j+1] if the j+1 mismatch occurs.
next[j+1] is the largest prefix and suffix for strKey from 0 to j:
#:(#: Here is a tag, which will be used later) We know A1 = A2, so is A1 and A2 equal after adding a character back? We have to discuss the following points:
(1) If str [k]== str [j], it is obvious that our next[j+1] is directly equal to k+1.
To write in code is next[++ j]=+k;
(2) If str [k]!= str [j], then we can only use the longest B1, B3 prefix and suffix known except A1, A2 to do the article.
So is B1 and B3 equal after adding one character to the back?
Because next[k] = the index of the green color block, let's first move k = next[k] to the position of the green color block, so that we can recursively call the logic at the "#:" tag.
Since the next array before j+1 is assumed to have been solved, the above recursion will always end and the value of next[j+1] will be obtained.
The only thing we lack is the initial conditions.
next[0] = -1, k = -1, j = 0
Another special case is that when k is -1, the recursion can not continue. At this time, next[j+1] should be equal to 0, that is to say, J should be returned to the first place.
That is next[j+1] = 0; it can also be written as next [+ + j] = + k;
public static int[] getNext(String ps)
{
char[] strKey = ps.toCharArray();
int[] next = new int[strKey.length];
// initial condition
int j = 0;
int k = -1;
next[0] = -1;
// Inference of j+1 bit from known pre-j bits
while (j < strKey.length - 1)
{
if (k == -1 || strKey[j] == strKey[k])
{
next[++j] = ++k;
}
else
{
k = next[k];
}
}
return next;
}Now look at this code, there should be no problem.
Optimize:
Careful friends should find out that there is such a sentence on it:
(1) If str [k]== str [j], it is obvious that our next[j+1] is directly equal to k+1. Writing in code is next [++ j]= + K.
But we know that the j+1 is mismatched. If we retreat J and find that the new j (that is, the + + k at this time) is equal to the j before retreat, it must also be mismatched. So we have to move on and back.
public static int[] getNext(String ps)
{
char[] strKey = ps.toCharArray();
int[] next = new int[strKey.length];
// initial condition
int j = 0;
int k = -1;
next[0] = -1;
// Inference of j+1 bit from known pre-j bits
while (j < strKey.length - 1)
{
if (k == -1 || strKey[j] == strKey[k])
{
// If str [j + 1]== str [k + 1], regression still mismatches, so continue regression
if (str[j + 1] == str[k + 1])
{
next[++j] = next[++k];
}
else
{
next[++j] = ++k;
}
}
else
{
k = next[k];
}
}
return next;
}Template
#include <cstring>
#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
using namespace std;
const int maxn=1e7+7;
const int INF=0x3f3f3f3f;
#define M 50015
int next1[maxn];
char str[maxn],mo[maxn];
int ans;
void getnext()
{
int i=0,j=-1,m=strlen(mo);
while(i<m){
if(j==-1||mo[i]==mo[j])
next1[++i]=++j;
else
j=next1[j];
}
}
int kmp()
{
int i=0,j=0,n=strlen(str),m=strlen(mo);
while(i<n){
if(j==-1||str[i]==mo[j])
i++,j++;
else
j=next1[j];
if(j==m)
ans++;
}
return ans;
}
int main()
{
int t;
cin>>t;
while(t--){
ans=0;
scanf("%s%s",mo,str);
next1[0]=-1;
getnext();
printf("%d\n",kmp());
}
}Example
A:HDU-1711 Number Sequence kmp algorithm template can be tapped directly. Attention should be paid to the location of i-m+1, AC code:
#include <cstring>
#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
using namespace std;
const int maxn=1e7+7;
const int INF=0x3f3f3f3f;
#define M 50015
int next1[maxn];
int str[maxn],mo[maxn];
int ans;
int n,m;
void getnext()
{
int i=0,j=-1;
while(i<m){
if(j==-1||mo[i]==mo[j])
next1[++i]=++j;
else
j=next1[j];
}
}
int kmp()
{
int i=0,j=0;
while(i<n){
if(j==-1||str[i]==mo[j])
i++,j++;
else
j=next1[j];
if(j==m)
return i-m+1;
}
return -1;
}
int main()
{
int t;
cin>>t;
while(t--){
ans=0;
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++)
scanf("%d",&str[i]);
for(int i=0;i<m;i++)
scanf("%d",&mo[i]);
next1[0]=-1;
getnext();
printf("%d\n",kmp());
}
}B:HDU-1686 Oulipo No tragedy any impurities of the most pure template, AC code:
#include <cstring>
#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
using namespace std;
const int maxn=1e7+7;
const int INF=0x3f3f3f3f;
#define M 50015
int next1[maxn];
char str[maxn],mo[maxn];
int ans;
void getnext()
{
int i=0,j=-1,m=strlen(mo);
while(i<m){
if(j==-1||mo[i]==mo[j])
next1[++i]=++j;
else
j=next1[j];
}
}
int kmp()
{
int i=0,j=0,n=strlen(str),m=strlen(mo);
while(i<n){
if(j==-1||str[i]==mo[j])
i++,j++;
else
j=next1[j];
if(j==m)
ans++;
}
return ans;
}
int main()
{
int t;
cin>>t;
while(t--){
ans=0;
scanf("%s%s",mo,str);
next1[0]=-1;
getnext();
printf("%d\n",kmp());
}
}C:HDU-2087 cut strip Ask for the number of substrings without overlapping parts in the parent string. Examine the understanding of mismatched arrays in KMP algorithm. If you want to "get rid" of the previous matching field completely and make it not overlapping with the next field, you only need to transfer the last matching point to 0 after mismatching, AC code:
#include <cstring>
#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
using namespace std;
const int maxn=1e7+7;
const int INF=0x3f3f3f3f;
#define M 50015
int next1[maxn];
char str[maxn],mo[maxn];
int ans;
void getnext()
{
int i=0,j=-1,m=strlen(mo);
while(i<m){
if(j==-1||mo[i]==mo[j])
next1[++i]=++j;
else
j=next1[j];
}
}
int kmp()
{
int i=0,j=0,n=strlen(str),m=strlen(mo);
while(i<n){
if(j==-1||str[i]==mo[j])
i++,j++;
else
j=next1[j];
if(j==m){
ans++;
j=0;
}
}
return ans;
}
int main()
{
while(1){
ans=0;
scanf("%s",str);
if(str[0]=='#')
break;
scanf("%s",mo);
next1[0]=-1;
getnext();
printf("%d\n",kmp());
}
return 0;
}D:HDU-3746 Cyclic Nacklace Minimum cyclic string problem. The main reason is to know that the length of a minimum loop string is len - next[len]. If len%(len - nxt[len])==0 and its len/(len - nxt[len])!=1, it means that it is already a cyclic string without the need for beads to output 0 directly. Otherwise, you need to add len - nxt[len] - (len - (len/(len - nxt[len])*(len - nxt[len]) * (len - NXT [len]) beads, which means that the total string length minus the number of cycles multiplied by the length of the cycle section is the number of beads remaining in the cycle section, minus the length of the rest of the cycle section by the minimum length of the beads added. . If you don't understand it, you can refer to it.( Cyclic Necklace The AC code:
#include <cstring>
#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
using namespace std;
const int maxn=1e7+7;
const int INF=0x3f3f3f3f;
#define M 50015
int next1[maxn];
char str[maxn],mo[maxn];
int ans;
void getnext()
{
int i=0,j=-1,m=strlen(mo);
while(i<m){
if(j==-1||mo[i]==mo[j])
next1[++i]=++j;
else
j=next1[j];
}
}
/*int kmp()
{
int i=0,j=0,n=strlen(str),m=strlen(mo);
while(i<n){
if(j==-1||str[i]==mo[j])
i++,j++;
else
j=next1[j];
if(j==m){
ans++;
}
}
return ans;
}*/
int main()
{
int t;
cin>>t;
while(t--){
ans=0;
scanf("%s",mo);
next1[0]=-1;
getnext();
int m=strlen(mo);
int x=m-next1[m];
if(x!=m&&m%x==0)
cout<<'0'<<endl;
else
cout<<x-(m%x)<<endl;
}
return 0;
}E:HDU-1358 Period i-next[i]== 0 and next[i]!=0, then i-next[i] and i/(i-next[i]) are required. AC code:
#include <cstring>
#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
using namespace std;
const int maxn=1e7+7;
const int INF=0x3f3f3f3f;
#define M 50015
int next1[maxn];
char str[maxn],mo[maxn];
int ans;
void getnext()
{
int i=0,j=-1,m=strlen(mo);
while(i<m){
if(j==-1||mo[i]==mo[j])
next1[++i]=++j;
else
j=next1[j];
}
}
/*int kmp()
{
int i=0,j=0,n=strlen(str),m=strlen(mo);
while(i<n){
if(j==-1||str[i]==mo[j])
i++,j++;
else
j=next1[j];
if(j==m){
ans++;
}
}
return ans;
}*/
int main()
{
int m,k=1;
while(cin>>m&&m!=0){
ans=0;
scanf("%s",mo);
next1[0]=-1;
getnext();
m=strlen(mo);
printf("Test case #%d\n",k++);
for(int i=1;i<=m;i++){
if(next1[i]!=0&&i%(i-next1[i])==0){
cout<<i<<' '<<i/(i-next1[i])<<endl;
}
}
cout<<endl;
}
return 0;
}F:POJ-2406 Power Strings The original intention of the question type is not much different from the first two questions. AC code:
#include <cstring>
#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
using namespace std;
const int maxn=1e7+7;
const int INF=0x3f3f3f3f;
#define M 50015
int next1[maxn];
char str[maxn],mo[maxn];
int ans;
void getnext()
{
int i=0,j=-1,m=strlen(mo);
while(i<m){
if(j==-1||mo[i]==mo[j])
next1[++i]=++j;
else
j=next1[j];
}
}
/*int kmp()
{
int i=0,j=0,n=strlen(str),m=strlen(mo);
while(i<n){
if(j==-1||str[i]==mo[j])
i++,j++;
else
j=next1[j];
if(j==m){
ans++;
j=0;
}
}
return ans;
}*/
int main()
{
while(cin>>mo&&mo[0]!='.'){
next1[0]=-1;
getnext();
int m=strlen(mo);
int x=m-next1[m];
if(m%x==0)
printf("%d\n",m/x);
else
cout<<1<<endl;
}
return 0;
}G:POJ-2752 Seek the Name, Seek the Fame The question is, given a string s, which length of s prefix is also the suffix of S. Firstly, the concepts of prefix and suffix are clarified. The prefix of the string s refers to the substring from the beginning character of s to any character of S. The suffix of the string s refers to the substring from any character of s to the last character of S. S is both its own prefix and its own suffix. This problem is solved by using the next [] array of KMP algorithm. First, for the input string s, the next [] array is computed. Then, further calculations are made based on the values of the next [] array. What you need to know is the definition of the next [] array. For the first character s[i], next[i] is defined as the maximum number of consecutive characters before the character s[i] and the character matching of the string s from the initial position. Match prefixes and suffixes from suffixes to prefixes. If the prefix matches the suffix, the next prefix matches the suffix string only in the prefix.
#include <cstring>
#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
using namespace std;
const int maxn=1e7+7;
const int INF=0x3f3f3f3f;
#define M 50015
int next1[maxn];
char str[maxn],mo[maxn];
int ans[maxn];
void getnext()
{
int i=0,j=-1,m=strlen(mo);
while(i<m){
if(j==-1||mo[i]==mo[j])
next1[++i]=++j;
else
j=next1[j];
}
}
/*int kmp()
{
int i=0,j=0,n=strlen(str),m=strlen(mo);
while(i<n){
if(j==-1||str[i]==mo[j])
i++,j++;
else
j=next1[j];
if(j==m){
ans++;
j=0;
}
}
return ans;
}*/
int main()
{
while(cin>>mo){
next1[0]=-1;
getnext();
int len=strlen(mo);
int p=0;
int t=next1[len];
while(t!=0){
ans[p++]=t;
t=next1[t];
}
for(int i=p-1;i>=0;i--)
cout<<ans[i]<<' ';
cout<<len<<endl;
}
return 0;
}H:POJ-3080 Blue Jeans Find the longest common continuous substring in multiple strings. If the length is the same, choose the one with the lowest dictionary order. Enumerates the length and start position of the string. Look again to see if the sequence exists in several strings. Simple KMP application questions, AC code:
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define N 150
char str[N][60];
int next[N];
void getnext(char a[],int n)
{
int i = 0,j = -1;
next[0] = -1;
while(i < n)
{
if(j == -1 || a[i] == a[j])
{
i++;
j++;
next[i] = j;
}
else
{
j = next[j];
}
}
}
int kmp(char a[],char b[],int n)
{
int i = 0,j = 0;
while(i < 60)
{
if(j == -1 || b[i] == a[j])
{
i++;j++;
}
else
{
j = next[j];
}
if(j == n)
return 1;
}
return 0;
}
int main()
{
int t,f;
scanf("%d",&t);
while(t--)
{
int n;
scanf("%d",&n);
char ans[N] = "Z";
for(int i = 0;i < n;i++)
{
scanf("%s",str[i]);
}
for(int len = 60;len >= 3;len--) //Length of strings
{
for(int i = 0;i <= 60 - len;i++) //The beginning character of a string
{
char sub[N] = {0};
strncpy(sub,str[0] + i,len); //Copy strings
int flag = 0;
getnext(sub,len);
for(int j = 1;j < n;j++)
{
if(!kmp(sub,str[j],len)) //kmp determines whether a string is in the current string
{
flag = 1;
break;
}
}
if(!flag && strcmp(ans,sub) > 0) //All have this common string, the dictionary order is the smallest.
{
strcpy(ans,sub);
}
}
f = 0;
if(ans[0] != 'Z')
{
printf("%s\n",ans);
f = 1;
break;
}
}
if(!f)
{
printf("no significant commonalities\n");
}
}
return 0;
}