The eleventh day of Python learning

aggregate

Hash

1. If an object cannot calculate the hash code, it cannot be put into the collection, and variable containers (list, collection, dictionary) cannot be put into the collection
2. The bottom layer of the set uses an efficient storage method: hash storage (hash storage). Therefore, the time efficiency of the set in element search is much higher than that of the list, which does not depend on the scale of the problem. It is a storage scheme with constant time complexity
3. List is not a hashable type
4. The storage mode of list tuple string is sequential storage. The advantage is that it can realize random access. The disadvantage is that it needs to judge whether the element exists, and the efficiency of searching the element is very low
5. Hash conflicts reduce efficiency
6. Baidu network disk speed second transmission principle: if there is no real upload, its server already has the file. Calculate the hash code locally. After uploading the hash code, after comparison, return the data: the user already has the file and changes the file name

Properties of sets

1. Dissimilarity, no duplicate elements in the set

2. Disorder. The order of elements in the set is determined by the hash code. The status of each element is the same, and the elements are disordered. Therefore, index operation cannot be supported

3. Certainty, an element, only belongs to and does not belong to the set, and there is no other ambiguity

4. The type of the collection is set

   Example:

   # The input strings are arranged randomly and duplicate elements are deleted
   set5 = set('hello')
   print(set5)
   # bool values also satisfy the set heterogeneity
   set2 = {True, False, True, True, False}
   print(set2)
   # Collections can store tuples
   set3 = {(1, 2, 3), 4, 5, 6)}
   print(set3)
   # Lists can store collections
   list4 = [set1, set2]
   print(list4)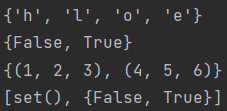
   

   

Creation of collections

A collection can be created by the literal syntax of {}, which consists of at least one element. If there is no element, it will not be an empty collection, but an empty dictionary

A collection can also be created by the built-in function set, which allows you to create an empty list

The elements in the collection must be of hashable type, that is, immutable type, which can calculate the type of hash code

Example:

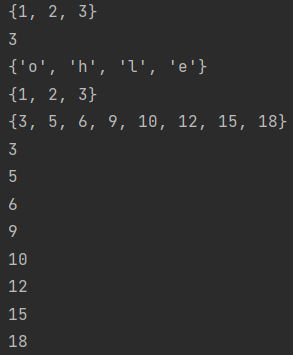
#Literal syntax for creating a collection (duplicate elements do not appear in the collection)

set1 = {1, 2, 3, 3, 3, 2}
print(set1)         # {1, 2, 3}
print(len(set1))    # 3

# Constructor syntax for creating collections (we'll talk about what constructors are later)

set2 = set('hello')
print(set2)         # {'h', 'l', 'o', 'e'}

# Convert a list into a collection (you can remove duplicate elements from the list)

set3 = set([1, 2, 3, 3, 2, 1])
print(set3)         # {1, 2, 3}

# Generative syntax for creating a collection (replace [] of list generative with {})

set4 = {num for num in range(1, 20) if num % 3 == 0 or num % 5 == 0}
print(set4)         # {3, 5, 6, 9, 10, 12, 15, 18}

# Loop traversal of collection elements

for elem in set4:
 print(elem)

Set operation

1. Member operation of set

   set1 = {1, 2, 3, 4, 5}
   set2 = {2, 4, 6, 8}
   print(1 in set1)
   print(1 not in set1)
   

   

2. Intersection union difference operation of sets

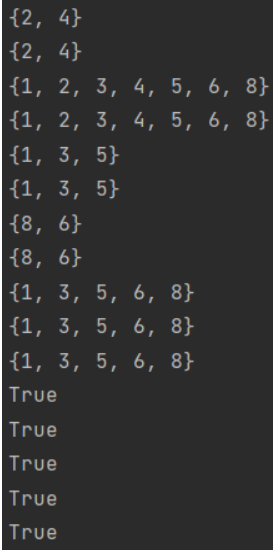
   set1 = {1, 2, 3, 4, 5}
   set2 = {2, 4, 6, 8}
   # intersection
   # Symbolic method
   print(set1 & set2)
   # Built in function method
   print(set1.intersection(set2))
   # Union
   # Symbolic method
   print(set1 | set2)
   # Built in function method
   print(set1.union(set2))
   # Difference set
   # The difference set does not satisfy the commutative law
   # Symbolic method
   print(set1 - set2)
   # Built in function method
   print(set1.difference(set2))
   # Symbolic method
   print(set2 - set1)
   # Built in function method
   print(set2.difference(set1))
   # Symmetry difference
   # Symmetric difference satisfies commutative law
   # Symbolic method
   print(set1 ^ set2)
   # Definition method
   print((set1 | set2) - (set1 & set2))
   # Built in function method
   print(set1.symmetric_difference(set2))
   
   set3 = {1, 2, 3, 4, 5, 6, 7, 8, 9}
   # Judge true subset
   # Symbolic method
   print(set1 < set3)
   # Built in function method
   print(set1.issubset(set3))
   # Judgment subset
   print(set1 <= set3)
   # Judgment superset
   # Symbolic method
   print(set3 > set2)
   # Built in function method
   print(set3.issuperset(set2))
   

Collection related operations

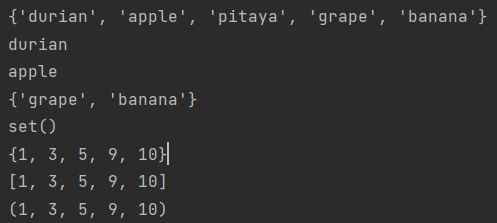
set1 = {'apple', 'banana', 'pitaya', 'apple'}

# Add element
# Due to the disorder of the collection, append and insert cannot be used, and the position of the element after adding is uncertain
set1.add('grape')
set1.add('durian')
print(set1)

# Delete element
# Deletes the specified element
set1.discard('pitaya')
# Randomly deletes the element, but returns the deleted value
print(set1.pop())
print(set1.pop())
print(set1)

# Empty element
set1.clear()
print(set1)

# Sets, tuples, and lists can be converted to each other
nums = [1, 1, 10, 10, 10, 5, 3, 9, 9]
# Convert list to collection
set2 = set(nums)
print(set2)
# Convert collection to list
list3 = list(set2)
print(list3)
# Convert list to tuple
tuple4 = tuple(list3)
print(tuple4)