Learning resources come from, Computer homework for a philosophy student (karenlyu21.github.io)

1. Background issues

The content of the previous section is mainly a static investigation of the social network, but the real social network is always evolving. One of the most important evolutionary phenomena is that some nodes that do not know each other may get to know each other at a certain point in time, corresponding to the establishment of a new edge in the network.

The acquaintance of two people has certain rules to follow, which is affected by "opportunity", "trust" and "motivation". When there is an intermediary (such as a common friend) between two strangers, this intermediary will greatly increase their chances of meeting, make it easier for them to trust each other, and sometimes have the motivation to get to know each other.

Two nodes get to know each other through the intermediary of their common friends, which is called "triadic closure". In class, Mr. Li introduced us a research based on big data, which verified the ternary closure principle with the help of e-mail exchange information in a University: the more common friends two people don't know each other, the higher the probability of their acquaintance after a period of time.

The class also mentioned that a refined version of the ternary closure principle is the "strong ternary closure principle". For a social network, we identify the edges into two categories, one indicating strong relationships and the other indicating weak relationships. If there is a strong relation between i and j, then there should be a strong relation between i and J.

The analysis here can also introduce the concept of "local bridge", that is, the nodes at both ends have no edges of "common friends". Based on the "strong ternary closure principle", we can deduce the "shortcut → weak relationship" theorem: in the network that identifies the strong weak relationship, if A node conforms to the strong ternary closure principle and has two strong friends (set as C and D), it must have A weak relationship with any shortcut connected friends (set as A and b). Otherwise, C or D must be the common friend of A and B, and the edge between A and B is no longer A shortcut.

One result of the evolution of social networks is "homogeneity": Friends (people close to each other) have some characteristic similarity, such as coming from the same place. We use "joining a 'Club' or 'Club' or" doing something "to describe a person's characteristics. When we consider the concept of "community" into the social network, the evolution of social network not only has the law of "ternary closure" principle, but also has two other laws:

• Principle of "social focal closure": two people get to know each other through a common community, which is called "community closure". In this closure, "birds of a feather flock together and people flock together", the homogeneity of social networks is strengthened.
• Principle of "membership closure": both community closure and ternary closure discuss the emergence of new friendship between two people. Besides, under what circumstances will a person join a club? Similar to the first two closures, when a person has several friends participating in a community, ta has more opportunities to know and trust the community and has more motivation to join it. In short, it is easier to join the community. This is the "member closure". In this kind of closure, "those who are close to each other are red and those who are close to each other are black", and the homogeneity of social networks can be strengthened.

2. Computing Practice: network evolution under the action of homogeneity

2.1 job description and algorithm ideas

The task of this assignment is to use programming to simulate the evolution of social networks based on the principle of three closures.

For the convenience of operation, we simplify the three closure principles into three threshold assumptions:

• Ternary closure: if two strangers have s or more common friends, they will become friends by the next point in time
• Community closure: if two strangers join f or more of the same clubs, they will become friends by the next point in time
• Member closure: if a person has m or more friends in a club, he will join the club before the next time point

Just as we can use adjacency matrix to represent the friend relationship in a social network, we can also use an attribution matrix to represent people's attribution relationship to social focus.

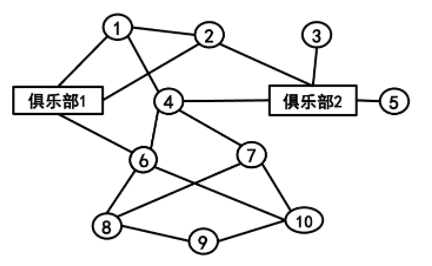
The above social network can be represented by the following two matrices:

• Adjacency matrix: represents the friend relationship between people;

• Attribution matrix: indicates the attribution relationship between people and associations. For example, the first row (1, 0) of the matrix indicates that person 1 joined community 1, but did not join community 2.

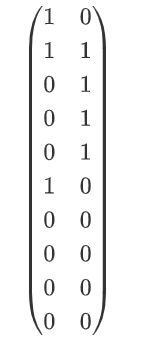
Based on the matrix of social network, the three closure principles can be expressed as the following mathematical relationship:

• Ternary closure: node i and node j establish an edge when A[i] ⋅ A[j] ≥ s;
• Community closure: node i and node j establish an edge when B[i] ⋅ B[j] ≥ f;
• Member closure: node i establishes an edge with community c when A[i] ⋅ B [] [c] ≥ m.

Given a social network, we investigate whether it meets the above three critical conditions, add the edges to generate the next round of social network, and then we do the same operation. So cycle until it is stable, and there is no new edge to add.

2.2 programming implementation and key points

Premise note: here, the adjacency matrix and attribution matrix adopt the social network matrix in the figure above.

First, we still need to call the function to read the data file and store the adjacency matrix and attribution matrix in numpy 2D arrays respectively. The former is A and the latter is B. s. The values of f and m are specified by the user.

def arrayGen_A(filename):
    f = open(filename, 'r')
    r_list = f.readlines()  
    f.close()
    A = []
    for line in r_list:
        if line == '\n':
            continue
        line = line.strip('\n')
        line = line.strip() 
        row_list = line.split() 
        for k in range(len(row_list)):
            row_list[k] = row_list[k].strip()
            row_list[k] = int(row_list[k])
        A.append(row_list)
    An = len(A[0])
    A = np.array(A)
    return A, An

def arrayGen_B(filename):
    f = open(filename, 'r')
    r_list = f.readlines() 
    f.close()
    B = []
    for line in r_list:
        if line == '\n':
            continue
        line = line.strip('\n')
        line = line.strip()  
        row_list = line.split()  
        for k in range(len(row_list)):
            row_list[k] = row_list[k].strip()
            row_list[k] = int(row_list[k])
        B.append(row_list)
    Bn = len(B[0])
    B = np.array(B)
    return B, Bn

filename_A = input('Please enter the file name of adjacency matrix:')
A, An = arrayGen_A(filename_A)
filename_B = input('Please enter the file name of the attribution matrix:')
B, Bn = arrayGen_B(filename_B)

s = int(input('Please enter the critical value of ternary closure (please enter an integer):'))
f = int(input('Please enter the critical value of community closure (please enter an integer):'))
m = int(input('Please enter the critical value of member closure (please enter an integer):'))

An example of an input value is as follows:

>>> Enter adjacency matrix file name:./a.txt
>>> Enter the file name of the attribution matrix:./b.txt
>>> Please enter the critical value of ternary closure (please enter an integer): 3
>>> Please enter the critical value of community closure (please enter an integer): 2
>>> Please enter the critical value of member closure (please enter an integer): 2

Then, I wrote the function edgeAdder to check the closure condition, which is convenient for repeated calling: input the data A, B and the values of s, f and m of the two matrices, and output the two matrices that meet the closure condition and add new edges.

def edgeAdder(A, B, an, bn, s, f, m):

Ternary closure: check the edges in the network one by one when A[i] × A[j] ≥ s, i.e. NP When dot (A[i], A[j]) > = s, node i establishes an edge with node j. At this time, I should not directly modify the adjacency matrix, otherwise it will affect the next test of member closure; I first store the edges that need to be added in a_ Alterers.

	A_alters = []
    B_alters = []
    for i in range(an):
        for j in range(i+1, an):
            if A[i][j] == 1:
                continue
            if np.dot(A[i], A[j]) >= s:  # Returns the dot product of two arrays
                A_alters.append([i, j])
                print('Ternary closure (person, person):\t%i %i' % (i, j))

Community closure: when NP When dot (B [i], B [J]) > = f, node i and node j establish an edge, which is stored in a_ Alterers.

    for i in range(an):
        for j in range(i+1, an):
            if A[i][j] == 1:
                continue
            if np.dot(B[i], B[j]) >=f:
                A_alters.append([i, j])
                print('Community closure (person, person):\t%i %i' % (i, j))

Member closure: when NP When dot (a [i], B [:, c]) > = m, node i establishes an edge with community c and stores it in B_ Alterers.

    for i in range(an):
        for c in range(bn):
            if B[i][c] == 1:
                continue
            if np.dot(A[i], B[:,c]) >= m:
                B_alters.append([i, c])
                print('Member closure (person, matter):\t%i %i' % (i, c))

According to a_ Alterers and B_alters, uniformly modify the matrix and add the edges.

    for item in A_alters:
        A[item[0]][item[1]] = 1
        A[item[1]][item[0]] = 1
    for item in B_alters:
        B[item[0]][item[1]] = 1
    return A, B, len(A_alters)+len(B_alters)

The content of the main program is to call the edgeAdder function round by round and add the edge of the addition until there is no edge to add and the evolution is over.

round = 1
print('Round 1:')
while True:
    A_new, B_new, alters = edgeAdder(A, B, An, Bn, s, f, m)
    if alters == 0:
        break
    else:
        A = A_new
        B = B_new
        round += 1
        print('The first %i Wheel:' % round)
print('Evolution is over!')

Round 1:
Ternary closure (person, person):    5 6
 Ternary closure (person, person):    7 9
 Member closure (person, matter):    0 1
 Member closure (person, matter):    3 0
 Round 2:
Community closure (person, person):    1 3
 Member closure (person, matter):    6 0
 Round 3:
Member closure (person, matter):    7 0
 Member closure (person, matter):    9 0
 Round 4:
Member closure (person, matter):    8 0
 Round 5:
Evolution is over!