catalogue
1. Introduction of red black tree
2. Basic properties of red black tree and definition of node
3. Rotation of red and black trees
4. Insertion of red black tree
Red black tree insertion summary:
7. Summary of red black tree and AVL tree
1. Introduction of red black tree
Red Black Tree is a self balancing binary search tree computer One used in science data structure , the typical use is to realize Associative array.
The red black tree was created by Rudolf Bayer It was called balanced binary B-trees at that time. Later, it was modified by Leo J. Guibas and Robert Sedgewick to today's "red black tree" in 1978.
Red black tree is a specialized AVL tree( balanced binary tree ), both maintain the balance of binary search tree through specific operations during insertion and deletion, so as to obtain high search performance.
Although it is complex, its worst-case running time is also very good, and it is efficient in practice: it can find, insert and delete in O(log n) time. Here n is the number of elements in the tree - from Baidu Encyclopedia
2. Basic properties of red black tree and definition of node
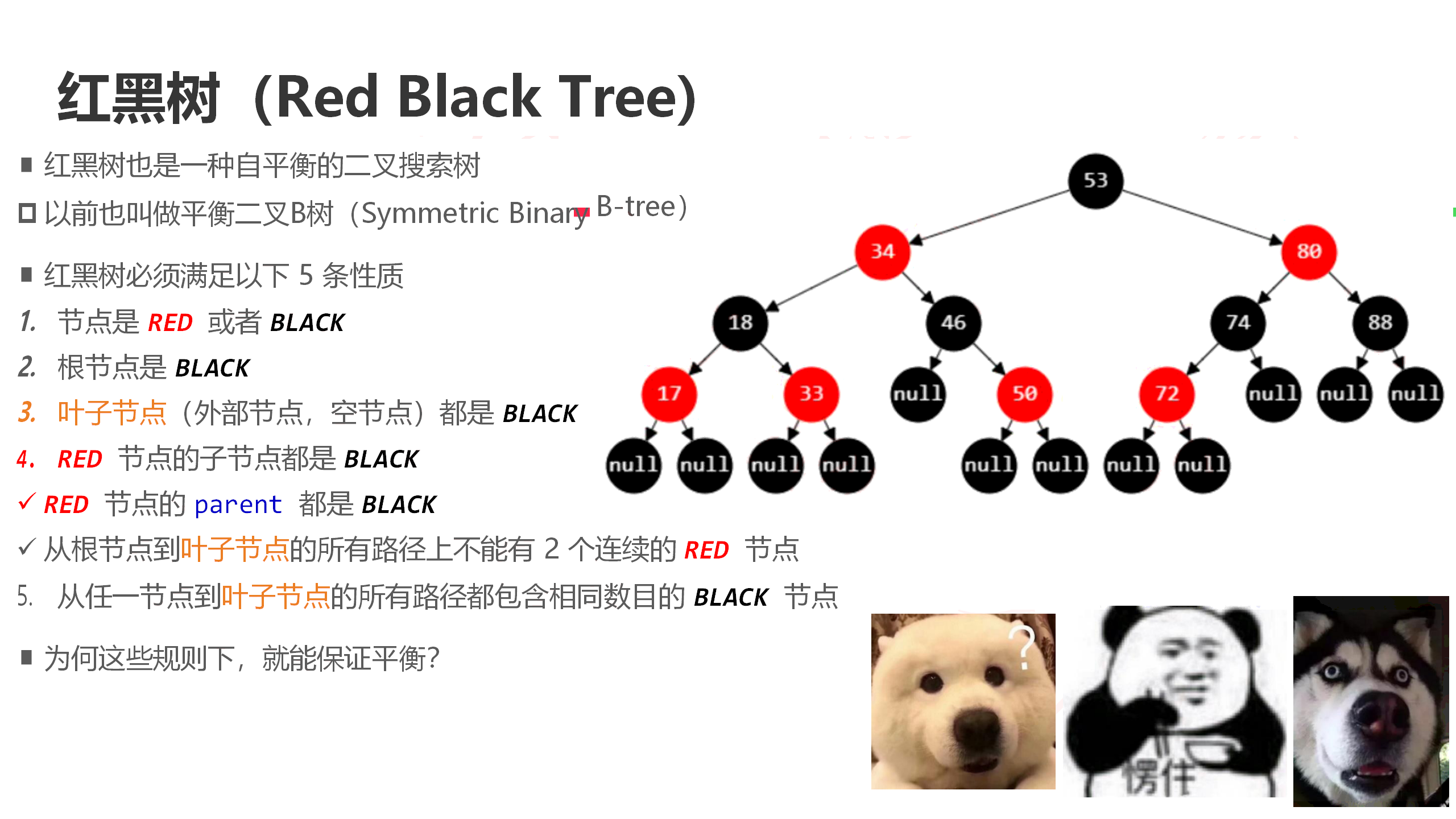
Red black tree is a binary search tree with red black nodes and self balancing. It must meet the following properties:
1. Each node is either red or black
2. The root node is black
3. If a node is red, its two child nodes are black
4. For each node, the simple path from this node to all its descendant leaf nodes contains the same number of black nodes
5. Each leaf node is black (the leaf node here refers to the empty node)
From property 5, we can infer that if a node has a sunspot node, then the node must have two children
Let's explain the problem in the picture:
From property 3, we can conclude that there are no continuous red nodes in the red black tree. According to property 4, we can conclude that the number of black nodes in all paths is the same.
We assume that the number from the root node to the leaf node is N, then the shortest path is all composed of black nodes, that is, the length is N
The longest path is composed of red and black alternately. In this path, the number of red nodes and black tree nodes is the same. According to property 4, we can get that the length of the longest path is 2N, so the longest path in the black tree will not exceed twice the shortest path, so an approximate balance is achieved.
Let's judge whether a tree is a red black tree:
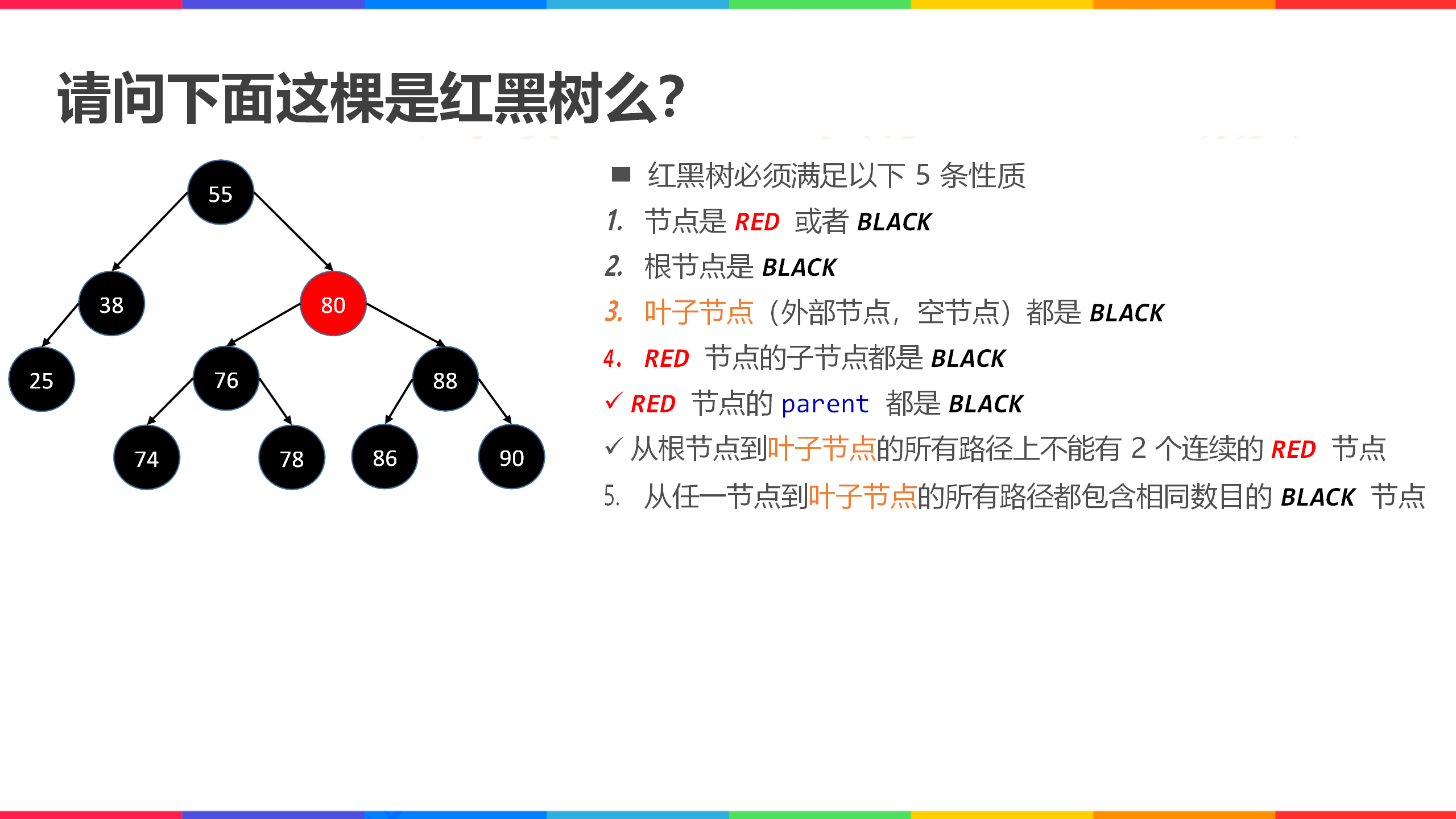
Obviously, this tree is not a red black tree. There are two paths from root node 55 to 38, one is to empty and the other is to 25. Obviously, the number of black nodes in the two paths is different, one is 3 and the other is 2 So this tree is not a red black tree
2.2
If we want to insert a node, do we want it to be a red node or a black tree node? Obviously, it is a red node. If a black node is inserted, it will destroy the same number of black nodes in any path in the red black tree. In response to this situation, it becomes very troublesome for us to adjust the red black tree. Therefore, we want the inserted node to be a red node.
Corresponding node code:
enum Colour
{
RED,
BLACK,
};
template<class K,class V>
struct RBTreeNode
{
RBTreeNode(const pair<K,V>&kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_col(RED)
{}
RBTreeNode<K, V>* _left;//Left pointer
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;//Father pointer
pair<K, V>_kv;
Colour _col;//Each node must have a color
};3. Rotation of red and black trees
1. Left hand rotation:
Firstly, disconnect the relationship between node PL and right child node g, and point the reference of its right child node to node C2; Then, disconnect the relationship between node g and left child node C2, and point the application of the left child node of G to node pl.

2. Right hand rotation
Firstly, disconnect the relationship between node g and left child node PL, and point the reference of its left child node to node C2; Then, disconnect the relationship between node PL and right child node C2, and point the application of the right child node of PL to node G.

Corresponding
void RotateR(Node* parent)
{
Node* cur = parent->_left;
Node* curR = cur->_right;//Right subtree of cur
Node* pparent = parent->_parent;//Save parent's parent node
//Link the cur right subtree to the left of the parent
parent->_left = curR;
if (curR)
curR->_parent = parent;
//Connect the parent to the right side of cur
cur->_right = parent;
parent->_parent = cur;
//Link cur to pparent
if (pparent == nullptr)//cur becomes a new root
{
_root = cur;
cur->_parent = nullptr;
}
else//pparent is not root
{
cur->_parent = pparent;
if (parent == pparent->_left)//Parent is on the left side of the parent node
{
pparent->_left = cur;
}
else
{
pparent->_right = cur;
}
}
}
//Sinistral
void RotateL(Node* parent)//Sinistral
{
Node* cur = parent->_right;//The right becomes higher and cannot be empty
Node* curL = cur->_left;
Node* pprent = parent->_parent;
//curL is connected to the parent
parent->_right = curL;
if (curL)
curL->_parent = parent;
//Connect parent to cur
cur->_left = parent;
parent->_parent = cur;
//cur link to pprent
if (pprent == nullptr)//root
{
_root = cur;
cur->_parent = nullptr;
}
else//Not root
{
cur->_parent = pprent;
//Determine which side the link is on
if (pprent->_left == parent)
{
pprent->_left = cur;
}
else
{
pprent->_right = cur;
}
}
}4. Insertion of red black tree
Let's take a look at a picture and learn some nouns
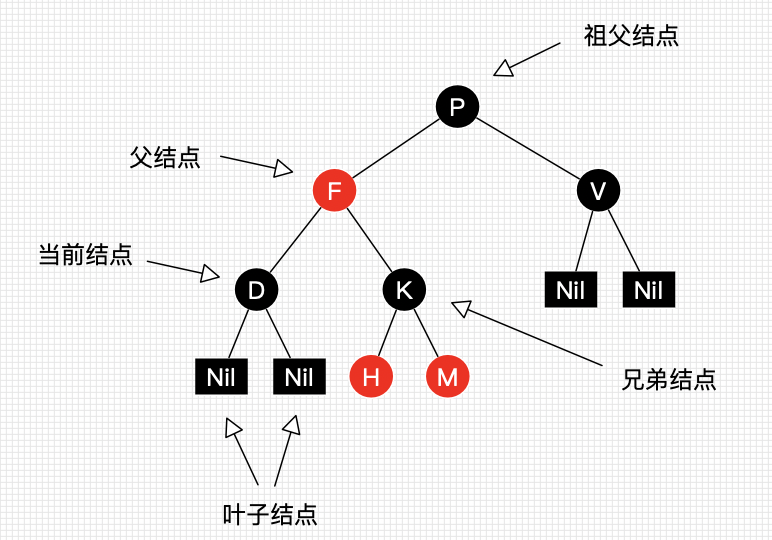
The idea of inserting red black tree is basically the same as that of searching binary tree, but there are more adjustment operations than searching binary tree.
1. Find the insertion position according to the size
2. Create the corresponding node and link with the parent
3. Adjust the red black tree
Insertion case I
The inserted is an empty tree, and the node is built directly and returned.
Insertion case II
The parent node of the inserted node is a black node: insert 66 this node
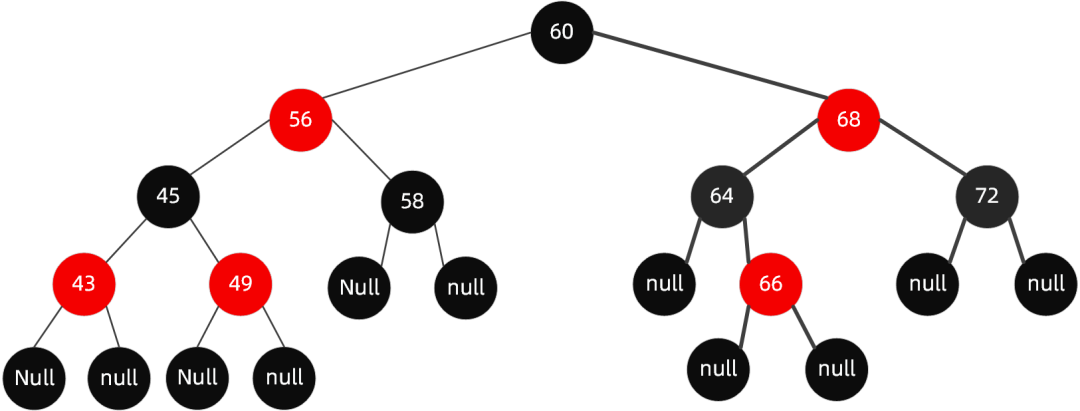
We found that his father was a black node. At this time, it did not violate the basic properties of black mangrove, and the insertion ended.
Insertion case III
After insertion, you need to change color without rotation, that is, the father of the inserted node is red and the uncle node is red.
Insert 51 this node
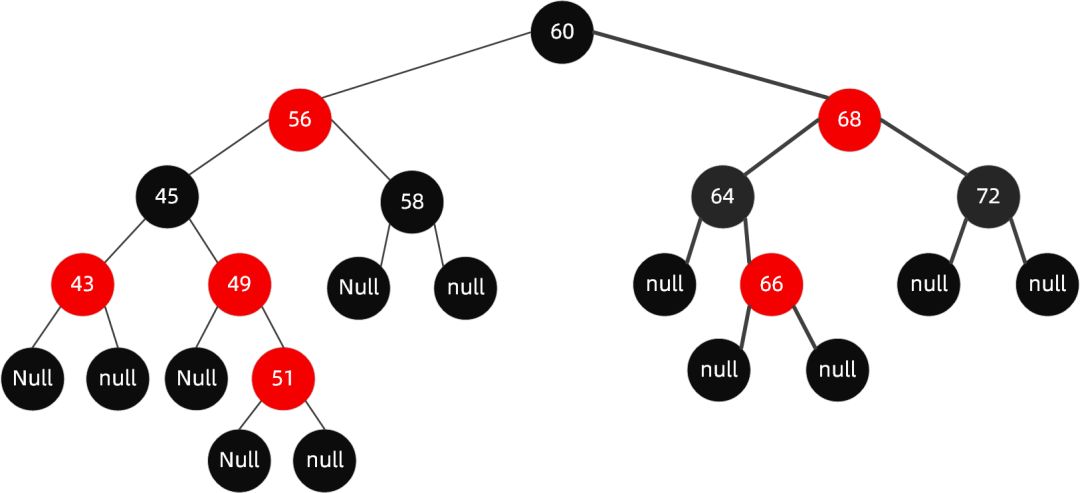
We find that his father node is red and his uncle node is red. At this time, we only need to turn the father node and uncle node black, turn the grandfather node red, and check whether it violates the rules of the red black tree from the grandfather node.
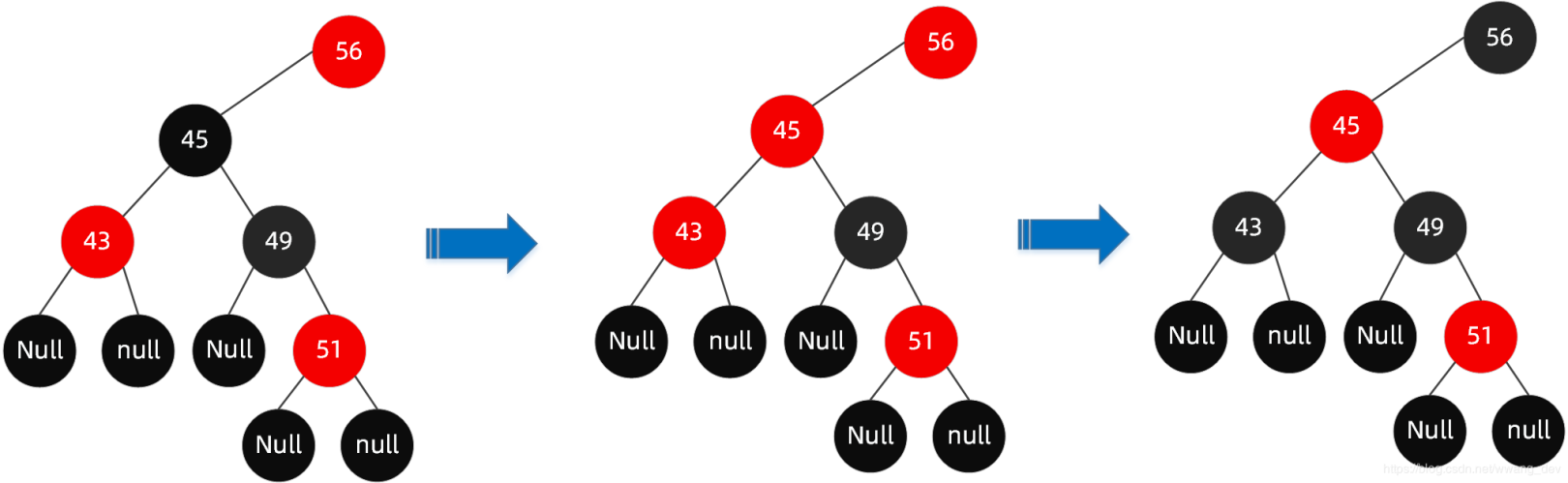
After the end, the whole tree is like this:
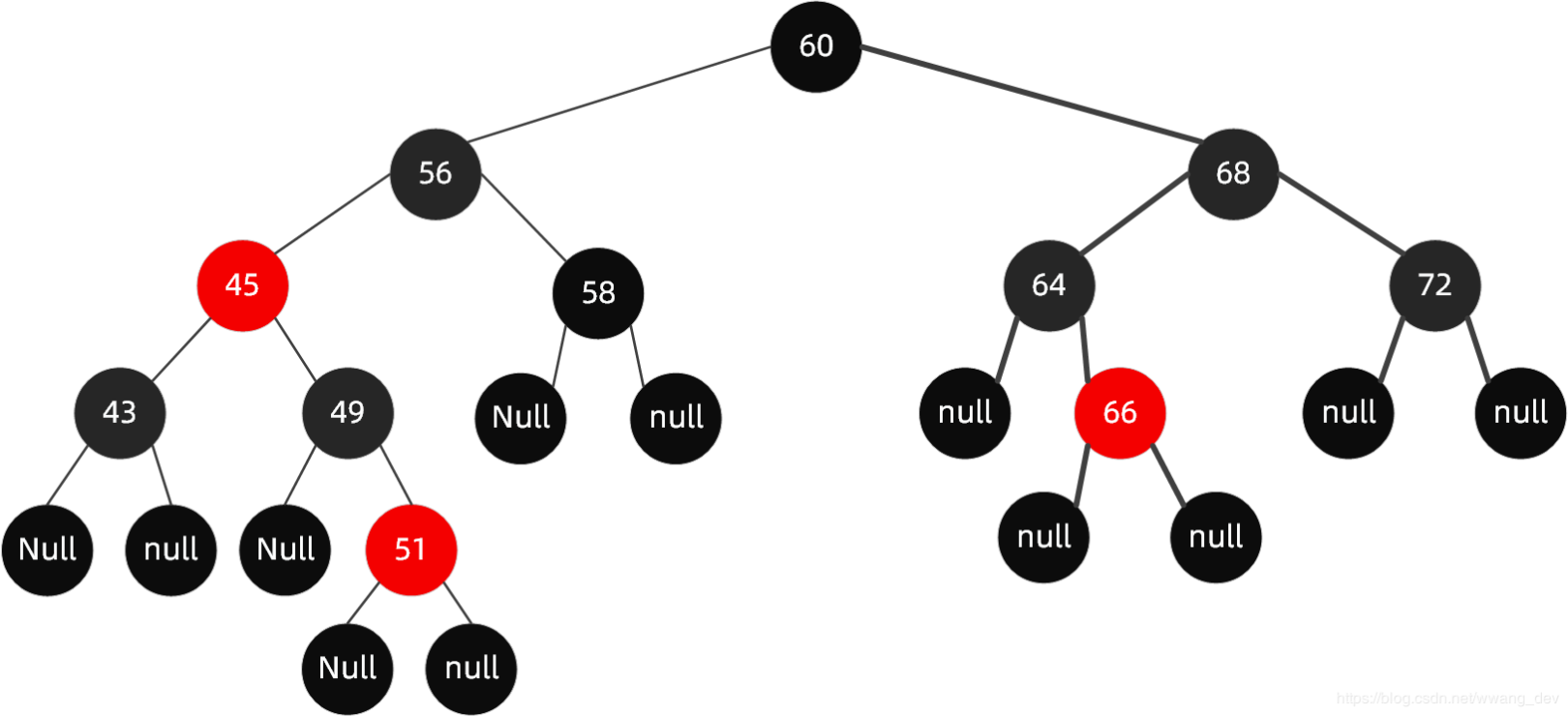
Insertion case IV
The inserted node is red or its parent is not black.
At this time, the insertion can be divided into four cases:
Case 1: the insertion node is the father's left child and the father is the grandfather's left child
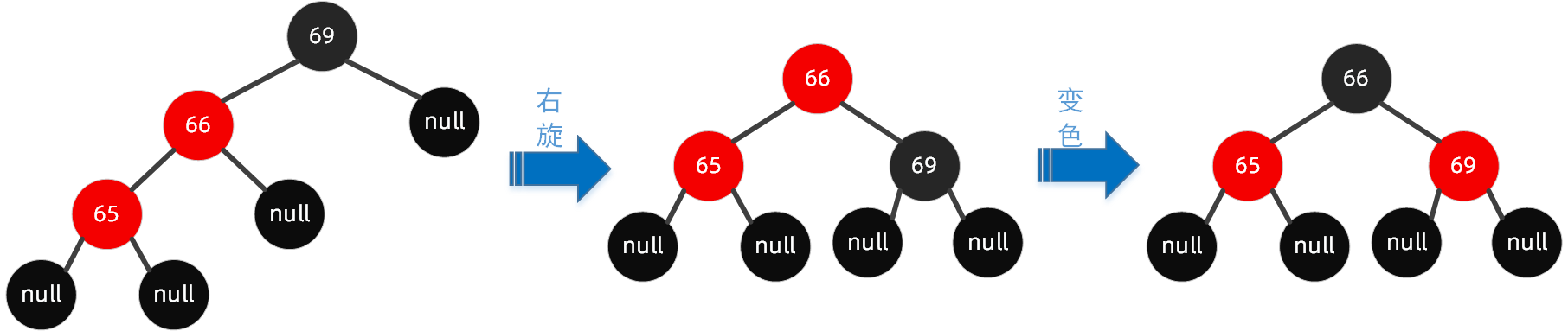
1. Insert 65 nodes
At this time, the parent node and the insertion node form two continuous red nodes, and at the same time, on the left (LL type), it is necessary to rotate the parent node to the right and change color. Color change: change the parent node to black and the grandfather node to red
Case 2: the insertion node is the right child of the father and the father is the left child of the grandfather.
Insert node 67:
At this time, the parent node and the insertion node form two continuous red nodes, and one on the left and one on the right is a broken line (LR), which needs double rotation and color change processing. First perform a left single rotation on the parent node and a right single rotation on the grandfather node. Set the color of the parent node to black and the grandfather node to red.

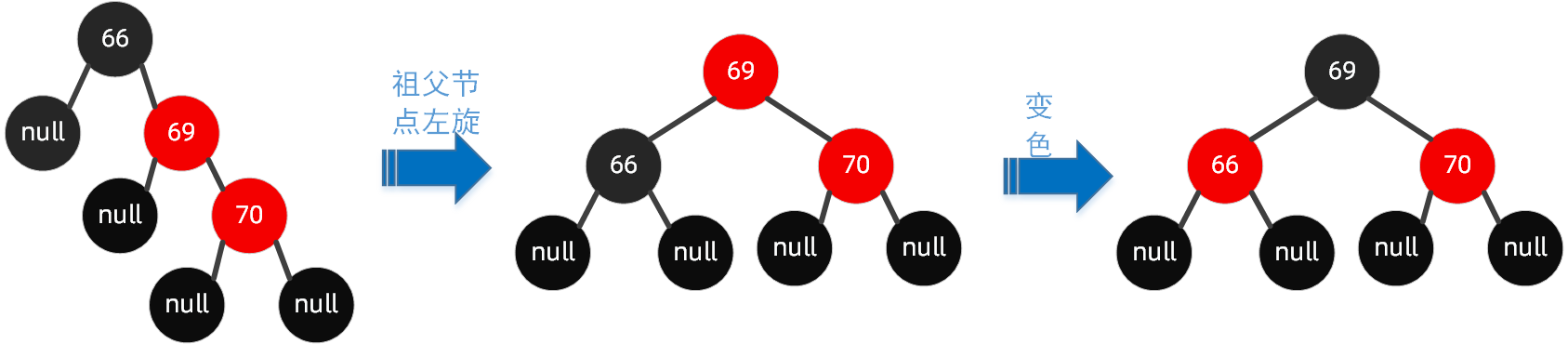
Case 3:
The parent node is the right child of the grandfather node and the insertion node is the right child of the parent node
Insert node 70:
At this time, the insertion node and the parent node form two red nodes, which are RR type on the right at the same time. We just need to carry out a left single rotation and color change treatment on them. Change the color of the father to black and the color of the grandfather node to red.
Case 4:
Father's Day is the right child of the grandfather node and the insertion node is the father's left child.

Insert 68 this node:
The parent node and the insertion node form two continuous red nodes, which belong to RL type. At this time, we only need to make a right single rotation for our father and a left single selection for our grandfather.
Color change: change the parent node to black and the grandfather node to red.

Red black tree insertion summary:
| No adjustment required | Just change color | Rotation + discoloration |
| The parent node of the inserted node is black | The father of the inserted node is red and the uncle node is red | The parent node is red and the uncle node is black. Insert the left child node (left rotation) |
| nothing | nothing | The parent node is red, the left node, and the uncle node is black. Insert the right child node (left and right double rotation) |
| nothing | nothing | The parent node is red and the uncle node is black. Insert the right child node (left rotation) |
| nothing | nothing | The parent node is a red right node, and the uncle node is a black one. Insert the left child node (right left double spin) |
Corresponding insertion code:
pair<Node* ,bool>Insert(const pair<K, V>& kv) {
if (!_root) {//Case 1 empty tree
_root = new Node(kv);
_root->_col = BLACK;
return make_pair(_root, true);
}
Node* parent = nullptr;
Node* cur = _root;//Find the corresponding position by the size of the value
while (cur) {
if (cur->_kv.first < kv.first) {
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first) {
parent = cur;
cur = cur->_left;
}
else {
return make_pair(cur, false);
}
}
Node*newnode = new Node(kv);
newnode->_col = RED;
if (parent->_kv.first < kv.first) {//Link with parent node
parent->_right= newnode;
newnode->_parent = parent;
}
else {
parent->_left = newnode;
newnode->_parent = parent;
}
cur = newnode;
while (parent&&parent->_col==RED)//The father exists and the father is red and needs to be handled
{
//The key is to see your uncle
Node* grandfather = parent->_parent;
if (parent == grandfather->_left) {//
Node* uncle = grandfather->_right;
//uncle exists and is red,
//Turn my grandfather red and my grandfather's two children black
if (uncle && uncle->_col == RED) {//Situation III
parent->_col = BLACK;
uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = grandfather->_parent;
}
else {//Uncle doesn't exist, or uncle doesn't exist
if (cur == parent->_left) {//Case 1 in case 4
RotateR(grandfather);
grandfather->_col = RED;
parent->_col = BLACK;
}
else {//Case 2 in case 4
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else {//It's grandpa's right
Node* uncle = grandfather->_left;//Situation III
if (uncle && uncle->_col == RED) {
uncle->_col = BLACK;
parent->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = grandfather->_parent;
}
else {
if (cur == parent->_right) {//Case 3 of case 4;
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else {//Minor case 4 in case 4
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;//In any case, the root node is black
return make_pair(newnode,true);
}5. Deletion of red black tree
The deletion of red black tree is much more complex than the insertion
The general steps are as follows:
1. Find the node according to the nature of binary search tree
2. Find a node to replace it
3. Adjust the red black tree to make it balanced
Let's first review the deletion of binary search tree:
Case 1: if the deleted node has no child nodes, it can be deleted directly
Case 2: if the deleted node has only one child node, replace the deleted node with a child node
Case 3: if the deleted node has two child nodes, replace the deleted node with a successor node (greater than the smallest node of the deleted node)
Case 3 can be converted to case 1 for processing.
Let's look at the deletion of red black tree
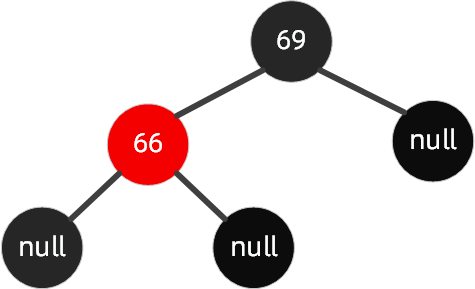
Case 1:
The node to be deleted is a red leaf node: delete 69 this red leaf node

You can delete it directly
Situation 2
Delete the black leaf node, the parent node is red, the brother node is black, and there is no red child node
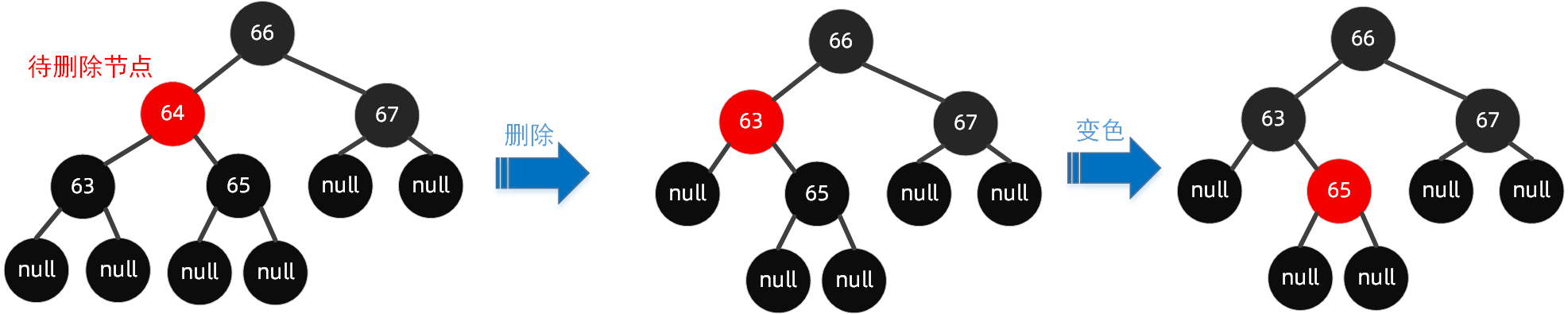
We want to delete the node 64, but we can change it to delete the leaf node 63. At this time, we only need to change the color to change the parent node to black and the brother node to red.
Case 3: the deleted node is a black leaf node, and the sibling node is black and has a red child node
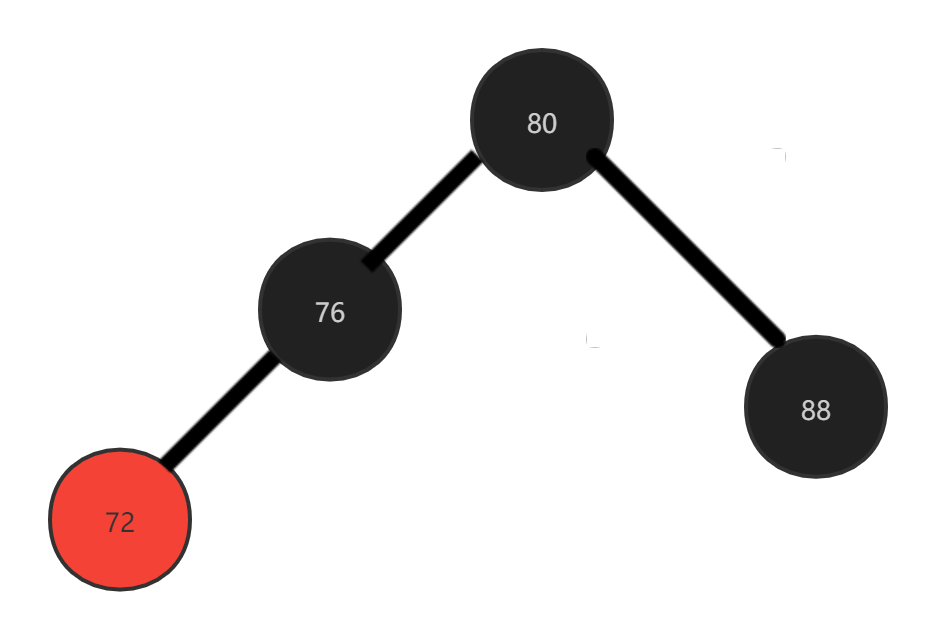
We want to delete 88 this black leaf node. After deletion, it is unbalanced. We found that his brother node is black and has a red child node, so we borrowed it from the brother node. How to borrow it? We found that the brother node and his red leaf node are in a straight line, so we just need to carry out a right single rotation and color change on 80.
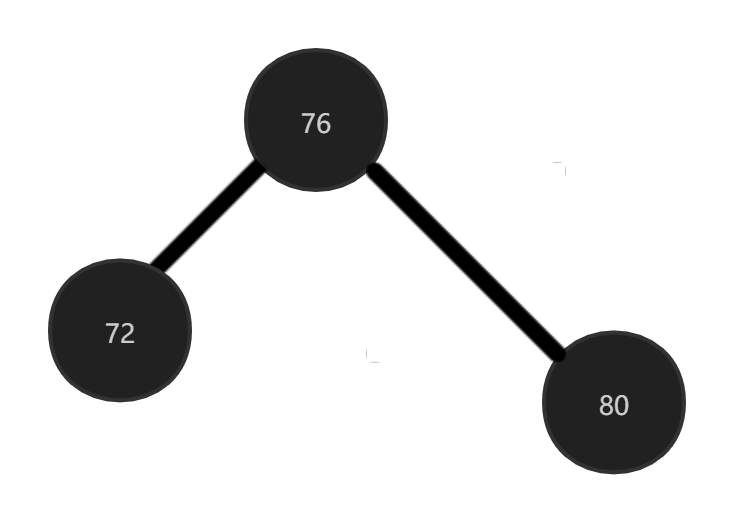
Discoloration: the rotated central node inherits the color of the original parent node, and the rotated left and right nodes are dyed into a black tree
There is another small case in case 3: the brother node and the red child node are not in a straight line: that is, on the right of the brother node
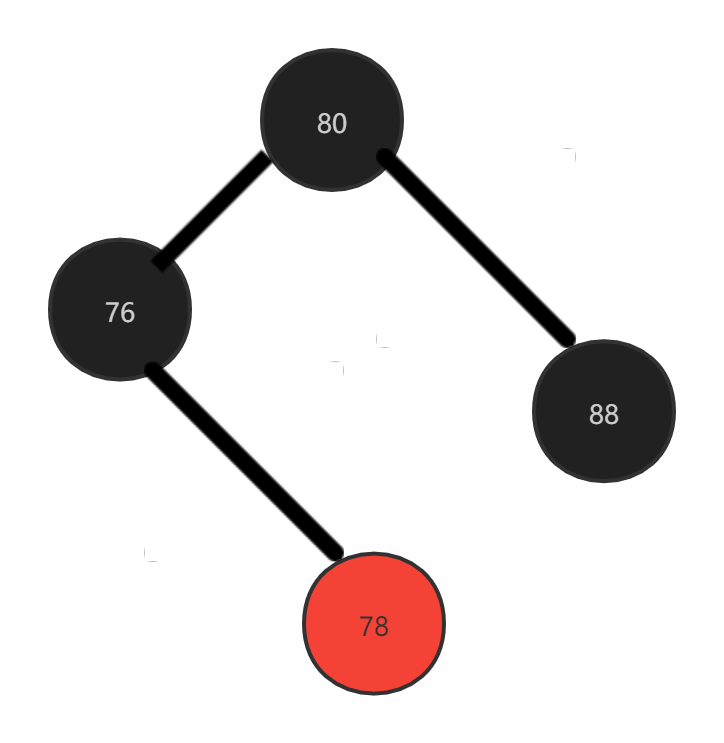
Similarly, delete 88 node. The difference between this situation and the above situation is that the red child node of the brother node is not on a certain straight line. At this time, we need to carry out double rotation processing, i.e. left and right double rotation + color change processing, that is, first carry out a left single rotation on the brother node and a right single rotation on the father node, To change color, you only need to inherit the color of the original parent node from the central node, and the left and right nodes turn black after rotation.
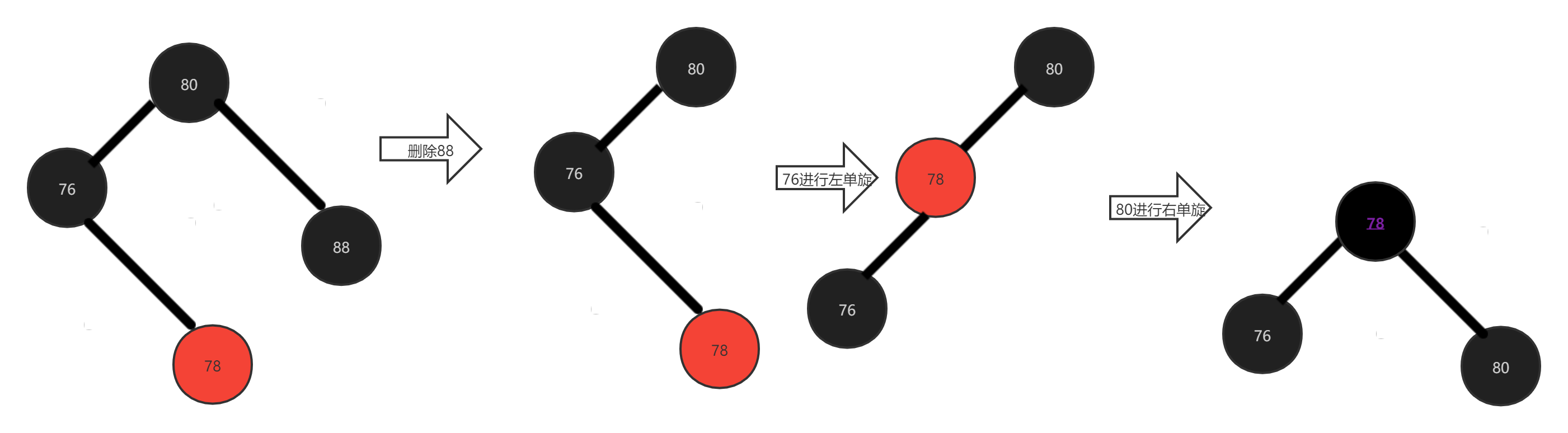
There are three cases. The left child whose deleted node is the Father also does the same, but the rotation mode is different. The old fellow can draw pictures on their own, if necessary, leave a message in the comments area.
Situation 4
Delete the black leaf node. The brother node is a black tree with two red nodes.
This situation can be divided into two cases: the deleted node is the father's left child and the deleted node is the father's right child. Here is only one example:
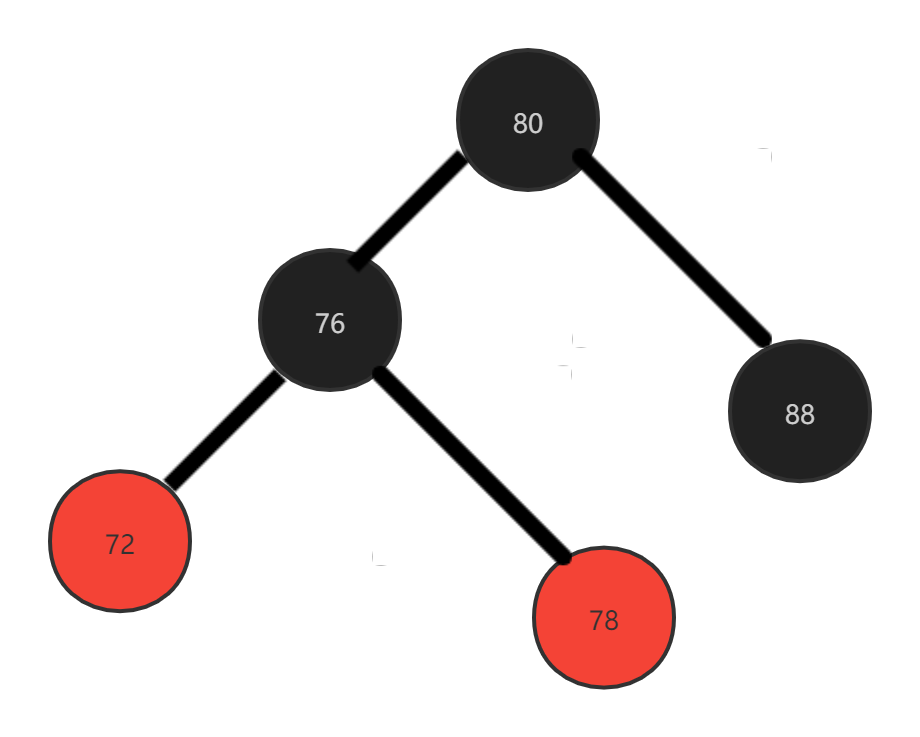
Here, we want to delete 88 node. At this time, its brother node has only {2 black tree nodes. At this time, we can perform double rotation or single rotation. Here, I rotate single rotation, that is, right single rotation.
Right single rotation is performed on the parent node. The rotated central node inherits the color of the parent node, and the left and right nodes turn black after rotation.
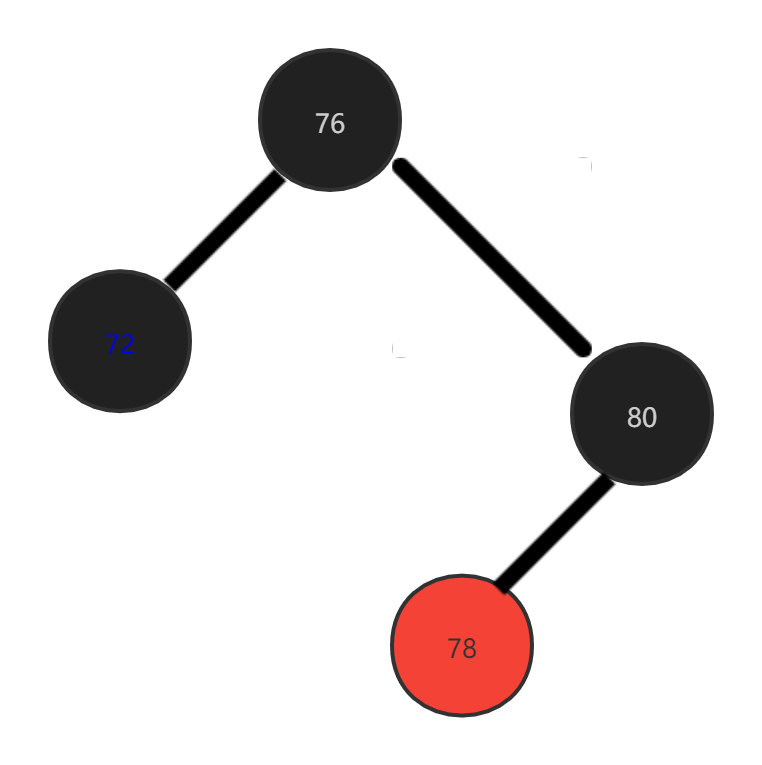
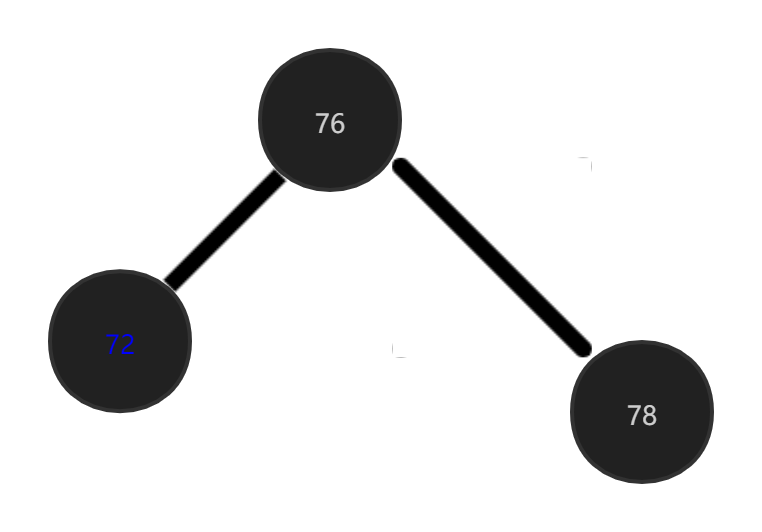
Case 5:
The deleted node is a black tree node and has a red sub node.
This situation is very simple. Replace the deleted node with a red child node and turn the red child node into black.

Delete 80 this node:
Case 6:
The deleted node is a leaf node, but the sibling node is a red node:
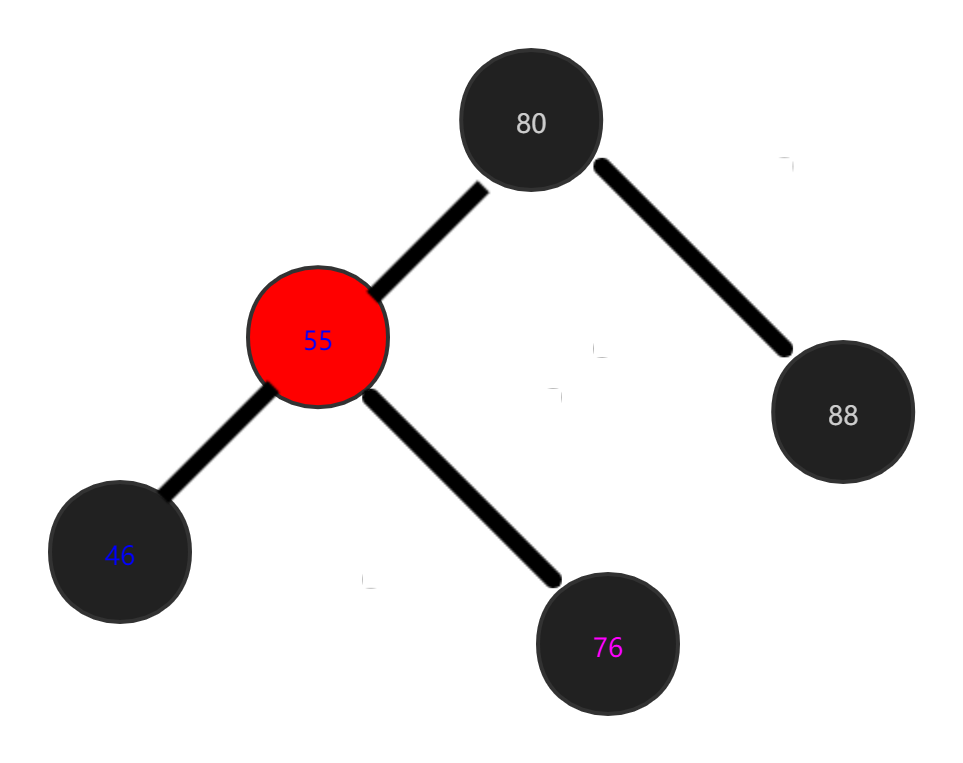
Delete 88 this node:
At this time, his brother node is red. Here, our 88 real black brother node is actually 76. Here, we force 88 and 76 to be brothers. We only need to make a right single spin on the parent node. The code written before calling and applying:
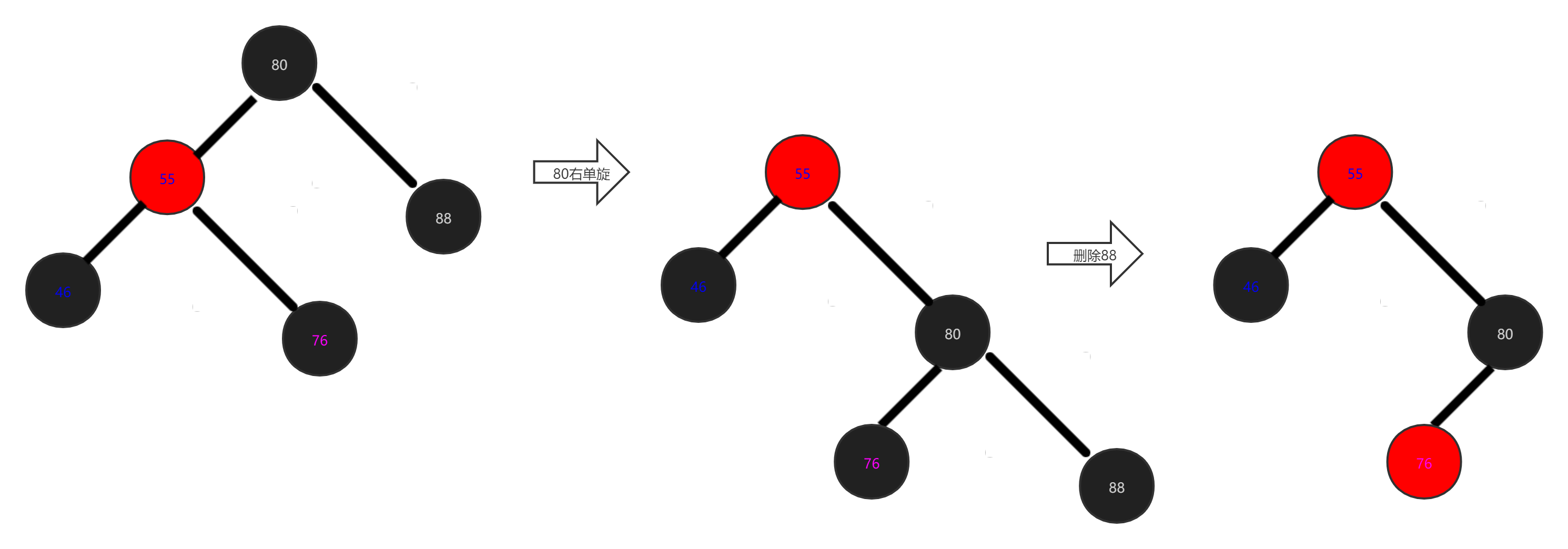
In the case of left single selection, the left parent of the deleted node is on the left, which is just the rotation direction is different. The old fellow can draw down their own paintings.
Case 7:
Delete the black leaf node, the parent node is black, the brother node is black, and there is no red child node:
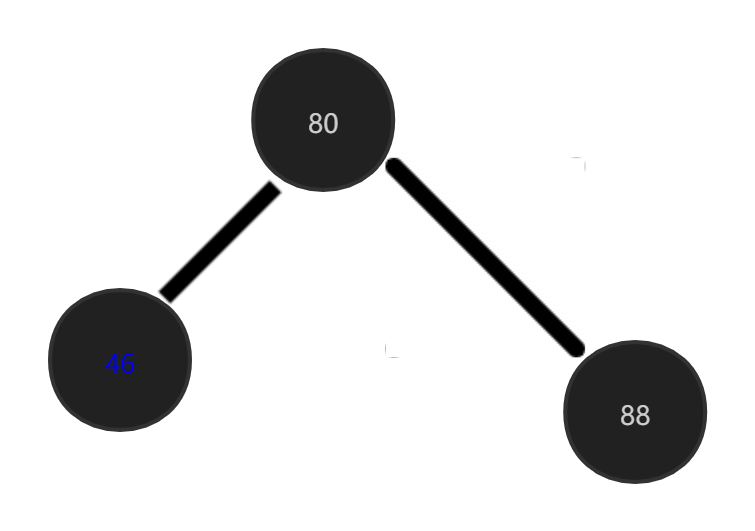
Delete 88 this node
First, turn the sibling node red and call the code above. Note that there may be nodes above node 80 in practice.
Corresponding code:
//Delete function
bool Erase(const K& key)
{
//Used to traverse a binary tree
Node* parent = nullptr;
Node* cur = _root;
//Used to mark the actual node to be deleted and its parent node
Node* delParentPos = nullptr;
Node* delPos = nullptr;
while (cur)
{
if (key < cur->_kv.first) //The given key value is less than the key value of the current node
{
//Go to the left subtree of this node
parent = cur;
cur = cur->_left;
}
else if (key > cur->_kv.first) //The given key value is greater than the key value of the current node
{
//Go to the right subtree of the node
parent = cur;
cur = cur->_right;
}
else //The node to be deleted was found
{
if (cur->_left == nullptr) //The left subtree of the node to be deleted is empty
{
if (cur == _root) //The node to be deleted is the root node
{
_root = _root->_right; //Let the right subtree of the root node be the new root node
if (_root)
{
_root->_parent = nullptr;
_root->_col = BLACK; //The root node is black
}
delete cur; //Delete original root node
return true;
}
else
{
delParentPos = parent; //Mark the parent node of the actual deleted node
delPos = cur; //Mark the node actually deleted
}
break; //Adjust the red black tree and actually delete the nodes
}
else if (cur->_right == nullptr) //The right subtree of the node to be deleted is empty
{
if (cur == _root) //The node to be deleted is the root node
{
_root = _root->_left; //Let the left subtree of the root node be the new root node
if (_root)
{
_root->_parent = nullptr;
_root->_col = BLACK; //The root node is black
}
delete cur; //Delete original root node
return true;
}
else
{
delParentPos = parent; //Mark the parent node of the actual deleted node
delPos = cur; //Mark the node actually deleted
}
break; //Adjust the red black tree and actually delete the nodes
}
else //The left and right subtrees of the node to be deleted are not empty
{
//Substitution deletion
//Find the node with the smallest key value in the right subtree of the node to be deleted as the actual deleted node
Node* minParent = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
minParent = minRight;
minRight = minRight->_left;
}
cur->_kv.first = minRight->_kv.first; //Change the key of the node to be deleted to the key of minRight
cur->_kv.second = minRight->_kv.second; //Change the value of the node to be deleted to the value of minRight
delParentPos = minParent; //Mark the parent node of the actual deleted node
delPos = minRight; //Mark the node actually deleted
break; //Adjust the red black tree and actually delete the nodes
}
}
}
if (delPos == nullptr) //delPos has not been modified, which means that the node to be deleted is not found
{
return false;
}
//Record the node to be deleted and its parent node (for subsequent actual deletion)
Node* del = delPos;
Node* delP = delParentPos;
//Adjust red black tree
if (delPos->_col == BLACK) //Black nodes are deleted
{
if (delPos->_left) //The node to be deleted has a red left child (cannot be black)
{
delPos->_left->_col = BLACK; //Turn the red left child black
}
else if (delPos->_right) //The node to be deleted has a red right child (cannot be black)
{
delPos->_right->_col = BLACK; //Turn the red right child black
}
else //The left and right of the node to be deleted are empty
{
while (delPos != _root) //It may be adjusted to the root node
{
if (delPos == delParentPos->_left) //The node to be deleted is the left child of its parent node
{
Node* brother = delParentPos->_right; //A sibling node is the right child of its parent node
//: brother is red
if (brother->_col == RED)
{
delParentPos->_col = RED;
brother->_col = BLACK;
RotateL(delParentPos);
//Need to continue processing
brother = delParentPos->_right; //Update brother (otherwise the code that executes other situations in this loop will make an error)
}
//: brother is black, and its left and right children are black or empty
if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))
&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK)))
{
brother->_col = RED;
if (delParentPos->_col == RED)
{
delParentPos->_col = BLACK;
break;
}
//Need to continue processing
delPos = delParentPos;
delParentPos = delPos->_parent;
}
else
{
//: brother is black, and its left child is red node, and its right child is black node or empty
if ((brother->_right == nullptr) || (brother->_right->_col == BLACK))
{
/* brother->_left->_col = BLACK;
brother->_col = RED;*/
RotateR(brother);
//Need to continue processing
brother = delParentPos->_right; //Update brother (otherwise an error will occur when executing the code in case 4 below)
}
//: brother is black, and its right child is red
brother->_col = delParentPos->_col;
delParentPos->_col = BLACK;
brother->_right->_col = BLACK;
RotateL(delParentPos);
break; //Situation four the adjustment will be finished after execution.
}
}
else //delPos == delParentPos->_ Right / / the node to be deleted is the left child of its parent node
{
Node* brother = delParentPos->_left; //A sibling node is the left child of its parent node
//: brother is red
if (brother->_col == RED) //brother is red
{
delParentPos->_col = RED;
brother->_col = BLACK;
RotateR(delParentPos);
//Need to continue processing
brother = delParentPos->_left; //Update brother (otherwise the code that executes other situations in this loop will make an error)
}
//: brother is black, and its left and right children are black or empty
if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))
&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK)))
{
brother->_col = RED;
if (delParentPos->_col == RED)
{
delParentPos->_col = BLACK;
break;
}
//Need to continue processing
delPos = delParentPos;
delParentPos = delPos->_parent;
}
else
{
//: brother is black, and its right child is red node, and its left child is black node or empty
if ((brother->_left == nullptr) || (brother->_left->_col == BLACK))
{
/*brother->_right->_col = BLACK;
brother->_col = RED;*/
RotateL(brother);
//Need to continue processing
brother = delParentPos->_left; //Update brother (otherwise an error will occur when executing the code in case 4 below)
}
//: brother is black and its left child is red
brother->_col = delParentPos->_col;
delParentPos->_col = BLACK;
brother->_left->_col = BLACK;
RotateR(delParentPos);
break; //Situation four the adjustment will be finished after execution.
}
}
}
}
}
//Actual deletion
if (del->_left == nullptr) //The left subtree of the actually deleted node is empty
{
if (del == delP->_left) //The actual deleted node is the left child of its parent node
{
delP->_left = del->_right;
if (del->_right)
del->_right->_parent = delP;
}
else //The actual deleted node is the right child of its parent node
{
delP->_right = del->_right;
if (del->_right)
del->_right->_parent = delP;
}
}
else //The right subtree of the actual deleted node is empty
{
if (del == delP->_left) //The actual deleted node is the left child of its parent node
{
delP->_left = del->_left;
if (del->_left)
del->_left->_parent = delP;
}
else //The actual deleted node is the right child of its parent node
{
delP->_right = del->_left;
if (del->_left)
del->_left->_parent = delP;
}
}
delete del; //Actually delete node
return true;
}6. Red black tree summary
To sum up, the self balancing treatment after red black tree deletion can be summarized as follows:
- Self digestion that you can handle
- If you can't handle it by yourself, ask your brother for help
- If brothers can't help, they can find distant relatives through their parents.
Haha, is it very similar to reality? When we have difficulties, we should first solve them ourselves. If we are unable to help, we should always find brothers and sisters. If we can't even help our brothers and sisters, we can go to distant relatives. The memory here should be easy to remember ~
7. Summary of red black tree and AVL tree


Finally, how can we verify the red black tree?
1. Each node is either red or black
2. The root node is black
3. If a node is red, its two child nodes are black
4. For each node, the simple path from this node to all its descendant leaf nodes contains the same number of black nodes
5. Each leaf node is black (the leaf node here refers to the empty node)
Back to the rule of red black tree, we only need to verify the first four points. The difficulty lies in verifying property 4. We can first count the number of black nodes in a path and see whether the number of black nodes is equal in other paths of the variable red black tree
Corresponding code:
bool CheckBlance() {
if (!_root) {
return true;
}
if (_root->_col == RED) {
cout << "The root node is red" << endl;
}
int blacknum = 0;
Node* left = _root;
while (left)
{
if (left->_col == BLACK) {
blacknum++;
}
left = left->_left;
}
int Count = 0;
return _CheckBlance(_root, blacknum, Count);
}
bool _CheckBlance(Node* root, int blackNum, int Count) {
if (!root) {
if (Count != blackNum) {
cout << "The number of black nodes is not equal" << endl;
return false;
}
return true;
}
if (root->_col == RED && root->_parent->_col == RED) {//Continuous red nodes
return false;
}
if (root->_col == BLACK) {
Count++;
}
return _CheckBlance(root->_left, blackNum, Count) && _CheckBlance(root->_right, blackNum, Count);
}Code summary:
#pragma once
#include<iostream>
using namespace std;
enum Colour
{
RED,
BLACK,
};
template<class K,class V>
struct RBTreeNode
{
RBTreeNode(const pair<K,V>&kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_col(RED)
{}
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
pair<K, V>_kv;
Colour _col;
};
template<class K,class V>
class RBTree {
typedef RBTreeNode<K, V> Node;
public:
pair<Node* ,bool>Insert(const pair<K, V>& kv) {
if (!_root) {
_root = new Node(kv);
_root->_col = BLACK;
return make_pair(_root, true);
}
Node* parent = nullptr;
Node* cur = _root;
while (cur) {
if (cur->_kv.first < kv.first) {
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first) {
parent = cur;
cur = cur->_left;
}
else {
return make_pair(cur, false);
}
}
Node*newnode = new Node(kv);
newnode->_col = RED;
if (parent->_kv.first < kv.first) {
parent->_right= newnode;
newnode->_parent = parent;
}
else {
parent->_left = newnode;
newnode->_parent = parent;
}
cur = newnode;
while (parent&&parent->_col==RED)//The father exists and the father is red and needs to be handled
{
//The key is to see your uncle
Node* grandfather = parent->_parent;
if (parent == grandfather->_left) {
Node* uncle = grandfather->_right;
//uncle exists and is red,
//Turn my grandfather red and my grandfather's two children black
if (uncle && uncle->_col == RED) {
parent->_col = BLACK;
uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = grandfather->_parent;
}
else {//Uncle doesn't exist, or uncle doesn't exist
if (cur == parent->_left) {//Single rotation
RotateR(grandfather);
grandfather->_col = RED;
parent->_col = BLACK;
}
else {
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else {//It's grandpa's right
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED) {
uncle->_col = BLACK;
parent->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = grandfather->_parent;
}
else {
if (cur == parent->_right) {
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else {
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return make_pair(newnode,true);
}
void RotateR(Node* parent)
{
Node* cur = parent->_left;
Node* curR = cur->_right;//Right subtree of cur
Node* pparent = parent->_parent;//Save parent's parent node
//Link the cur right subtree to the left of the parent
parent->_left = curR;
if (curR)
curR->_parent = parent;
//Connect the parent to the right side of cur
cur->_right = parent;
parent->_parent = cur;
//Link cur to pparent
if (pparent == nullptr)//cur becomes a new root
{
_root = cur;
cur->_parent = nullptr;
}
else//pparent is not root
{
cur->_parent = pparent;
if (parent == pparent->_left)//Parent is on the left side of the parent node
{
pparent->_left = cur;
}
else
{
pparent->_right = cur;
}
}
}
//Sinistral
void RotateL(Node* parent)//Sinistral
{
Node* cur = parent->_right;//The right becomes higher and cannot be empty
Node* curL = cur->_left;
Node* pprent = parent->_parent;
//curL is connected to the parent
parent->_right = curL;
if (curL)
curL->_parent = parent;
//Connect parent to cur
cur->_left = parent;
parent->_parent = cur;
//cur link to pprent
if (pprent == nullptr)//root
{
_root = cur;
cur->_parent = nullptr;
}
else//Not root
{
cur->_parent = pprent;
//Determine which side the link is on
if (pprent->_left == parent)
{
pprent->_left = cur;
}
else
{
pprent->_right = cur;
}
}
}
bool CheckBlance() {
if (!_root) {
return true;
}
if (_root->_col == RED) {
cout << "The root node is red" << endl;
}
int blacknum = 0;
Node* left = _root;
while (left)
{
if (left->_col == BLACK) {
blacknum++;
}
left = left->_left;
}
int Count = 0;
return _CheckBlance(_root, blacknum, Count);
}
bool _CheckBlance(Node* root, int blackNum, int Count) {
if (!root) {
if (Count != blackNum) {
cout << "The number of black nodes is not equal" << endl;
return false;
}
return true;
}
if (root->_col == RED && root->_parent->_col == RED) {//Continuous red nodes
return false;
}
if (root->_col == BLACK) {
Count++;
}
return _CheckBlance(root->_left, blackNum, Count) && _CheckBlance(root->_right, blackNum, Count);
}
//Delete function
bool Erase(const K& key)
{
//Used to traverse a binary tree
Node* parent = nullptr;
Node* cur = _root;
//Used to mark the actual node to be deleted and its parent node
Node* delParentPos = nullptr;
Node* delPos = nullptr;
while (cur)
{
if (key < cur->_kv.first) //The given key value is less than the key value of the current node
{
//Go to the left subtree of this node
parent = cur;
cur = cur->_left;
}
else if (key > cur->_kv.first) //The given key value is greater than the key value of the current node
{
//Go to the right subtree of the node
parent = cur;
cur = cur->_right;
}
else //The node to be deleted was found
{
if (cur->_left == nullptr) //The left subtree of the node to be deleted is empty
{
if (cur == _root) //The node to be deleted is the root node
{
_root = _root->_right; //Let the right subtree of the root node be the new root node
if (_root)
{
_root->_parent = nullptr;
_root->_col = BLACK; //The root node is black
}
delete cur; //Delete original root node
return true;
}
else
{
delParentPos = parent; //Mark the parent node of the actual deleted node
delPos = cur; //Mark the node actually deleted
}
break; //Adjust the red black tree and actually delete the nodes
}
else if (cur->_right == nullptr) //The right subtree of the node to be deleted is empty
{
if (cur == _root) //The node to be deleted is the root node
{
_root = _root->_left; //Let the left subtree of the root node be the new root node
if (_root)
{
_root->_parent = nullptr;
_root->_col = BLACK; //The root node is black
}
delete cur; //Delete original root node
return true;
}
else
{
delParentPos = parent; //Mark the parent node of the actual deleted node
delPos = cur; //Mark the node actually deleted
}
break; //Adjust the red black tree and actually delete the nodes
}
else //The left and right subtrees of the node to be deleted are not empty
{
//Substitution deletion
//Find the node with the smallest key value in the right subtree of the node to be deleted as the actual deleted node
Node* minParent = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
minParent = minRight;
minRight = minRight->_left;
}
cur->_kv.first = minRight->_kv.first; //Change the key of the node to be deleted to the key of minRight
cur->_kv.second = minRight->_kv.second; //Change the value of the node to be deleted to the value of minRight
delParentPos = minParent; //Mark the parent node of the actual deleted node
delPos = minRight; //Mark the node actually deleted
break; //Adjust the red black tree and actually delete the nodes
}
}
}
if (delPos == nullptr) //delPos has not been modified, which means that the node to be deleted is not found
{
return false;
}
//Record the node to be deleted and its parent node (for subsequent actual deletion)
Node* del = delPos;
Node* delP = delParentPos;
//Adjust red black tree
if (delPos->_col == BLACK) //Black nodes are deleted
{
if (delPos->_left) //The node to be deleted has a red left child (cannot be black)
{
delPos->_left->_col = BLACK; //Turn the red left child black
}
else if (delPos->_right) //The node to be deleted has a red right child (cannot be black)
{
delPos->_right->_col = BLACK; //Turn the red right child black
}
else //The left and right of the node to be deleted are empty
{
while (delPos != _root) //It may be adjusted to the root node
{
if (delPos == delParentPos->_left) //The node to be deleted is the left child of its parent node
{
Node* brother = delParentPos->_right; //A sibling node is the right child of its parent node
//: brother is red
if (brother->_col == RED)
{
delParentPos->_col = RED;
brother->_col = BLACK;
RotateL(delParentPos);
//Need to continue processing
brother = delParentPos->_right; //Update brother (otherwise the code that executes other situations in this loop will make an error)
}
//: brother is black, and its left and right children are black or empty
if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))
&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK)))
{
brother->_col = RED;
if (delParentPos->_col == RED)
{
delParentPos->_col = BLACK;
break;
}
//Need to continue processing
delPos = delParentPos;
delParentPos = delPos->_parent;
}
else
{
//: brother is black, and its left child is red node, and its right child is black node or empty
if ((brother->_right == nullptr) || (brother->_right->_col == BLACK))
{
/* brother->_left->_col = BLACK;
brother->_col = RED;*/
RotateR(brother);
//Need to continue processing
brother = delParentPos->_right; //Update brother (otherwise an error will occur when executing the code in case 4 below)
}
//: brother is black, and its right child is red
brother->_col = delParentPos->_col;
delParentPos->_col = BLACK;
brother->_right->_col = BLACK;
RotateL(delParentPos);
break; //Situation four the adjustment will be finished after execution.
}
}
else //delPos == delParentPos->_ Right / / the node to be deleted is the left child of its parent node
{
Node* brother = delParentPos->_left; //A sibling node is the left child of its parent node
//: brother is red
if (brother->_col == RED) //brother is red
{
delParentPos->_col = RED;
brother->_col = BLACK;
RotateR(delParentPos);
//Need to continue processing
brother = delParentPos->_left; //Update brother (otherwise the code that executes other situations in this loop will make an error)
}
//: brother is black, and its left and right children are black or empty
if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))
&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK)))
{
brother->_col = RED;
if (delParentPos->_col == RED)
{
delParentPos->_col = BLACK;
break;
}
//Need to continue processing
delPos = delParentPos;
delParentPos = delPos->_parent;
}
else
{
//: brother is black, and its right child is red node, and its left child is black node or empty
if ((brother->_left == nullptr) || (brother->_left->_col == BLACK))
{
/*brother->_right->_col = BLACK;
brother->_col = RED;*/
RotateL(brother);
//Need to continue processing
brother = delParentPos->_left; //Update brother (otherwise an error will occur when executing the code in case 4 below)
}
//: brother is black and its left child is red
brother->_col = delParentPos->_col;
delParentPos->_col = BLACK;
brother->_left->_col = BLACK;
RotateR(delParentPos);
break; //Situation four the adjustment will be finished after execution.
}
}
}
}
}
//Actual deletion
if (del->_left == nullptr) //The left subtree of the actually deleted node is empty
{
if (del == delP->_left) //The actual deleted node is the left child of its parent node
{
delP->_left = del->_right;
if (del->_right)
del->_right->_parent = delP;
}
else //The actual deleted node is the right child of its parent node
{
delP->_right = del->_right;
if (del->_right)
del->_right->_parent = delP;
}
}
else //The right subtree of the actual deleted node is empty
{
if (del == delP->_left) //The actual deleted node is the left child of its parent node
{
delP->_left = del->_left;
if (del->_left)
del->_left->_parent = delP;
}
else //The actual deleted node is the right child of its parent node
{
delP->_right = del->_left;
if (del->_left)
del->_left->_parent = delP;
}
}
delete del; //Actually delete node
return true;
}
private:
Node* _root=NULL;
};reference material: