Algorithm learning Chapter 1

Palindrome number

Difficulty: simple

Title:
Give you an integer X. if x is a palindrome integer, return true; Otherwise, false is returned.
Palindromes are integers whose positive (left to right) and reverse (right to left) reads are the same. For example, 121 is a palindrome, not 123.

Idea:
First convert an integer to a string, and then flip the string to determine whether the string is the same.

Don't say much, just do it

// An highlighted block
 public boolean isPalindrome(int x) {
        String strX = String.valueOf(x);
        String strF = reverse(strX);
        return strX.equals(strF);
  }

Method 1: use StringBuffer

 /**
     * String flip
     * @param str
     * @return
     */
    private String reverse(String str){
        StringBuffer sb = new StringBuffer(str);
        sb.reverse();
        return sb.toString();
    }

results of enforcement

Using Stringbuffer to flip strings is a perfect solution, but it is obvious that the memory consumption is relatively large.

Method 2: use for loop + StringBuilder

/**
     * String flip
     * @param str
     * @return
     */
    private String reverse1(String str){
        StringBuilder sb = new StringBuilder();
        for(int i = str.length() - 1; i >= 0; i-- ){
            sb.append(str.charAt(i));
        }
        return sb.toString();
    }

results of enforcement

It is found that the running speed and memory consumption are similar to that of StringBuffer, and both methods can be used.

Method 3: array flip

 /**
     * Convert a String string into a character array. After reversing the character array, convert the array into a String object
     * @param str
     * @return
     */
    private String reverse3(String str){
        char[] chars = str.toCharArray();
        for (int x = 0, y = chars.length - 1; x < y; x++, y--) {
            char temp = chars[x];
            chars[x] = chars[y];
            chars[y] = temp;
        }
        return new String(chars);
    }

results of enforcement

The results show that the running speed and memory consumption are slightly better than the two methods.

Since then, my thoughts have been shared. Let's see what good methods the big guys have.

Advanced solution I: mathematical solution

Comparison by rounding and remainder
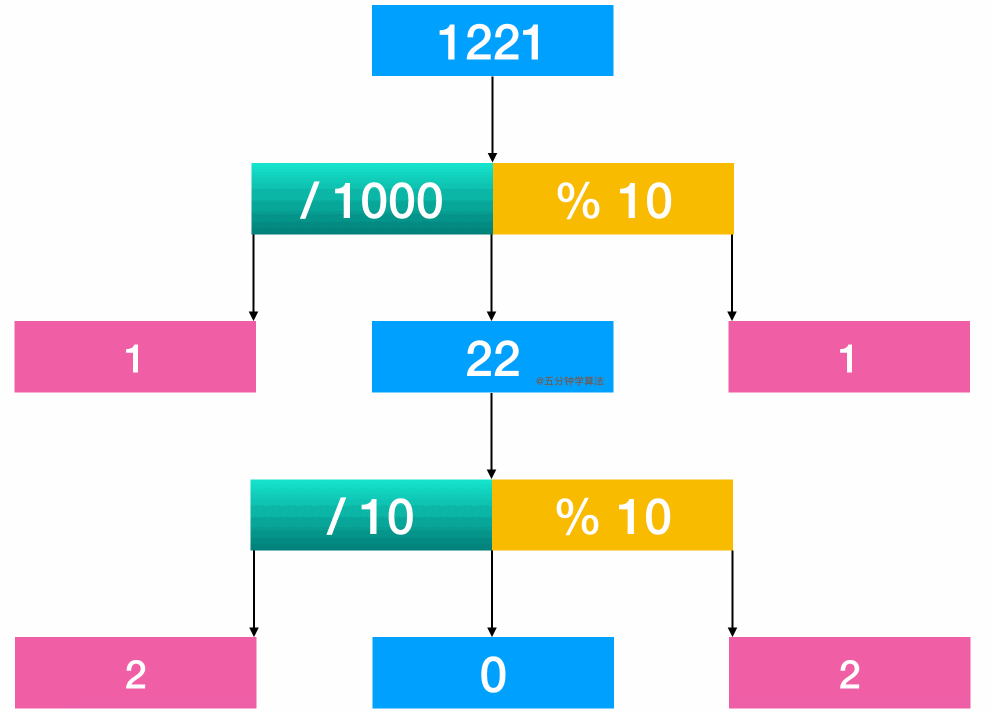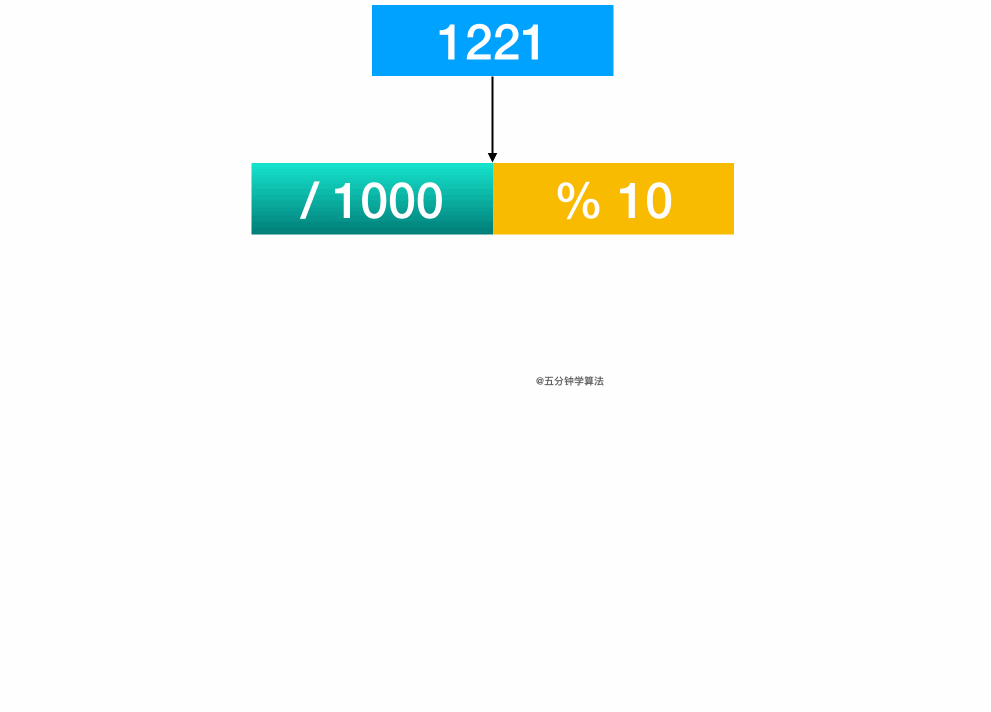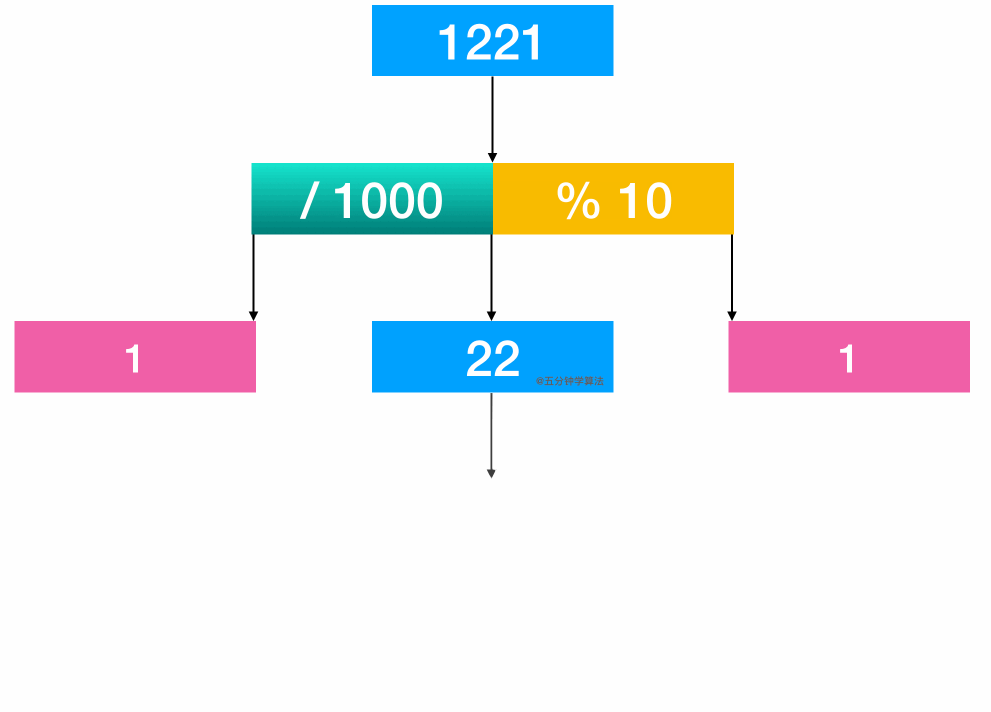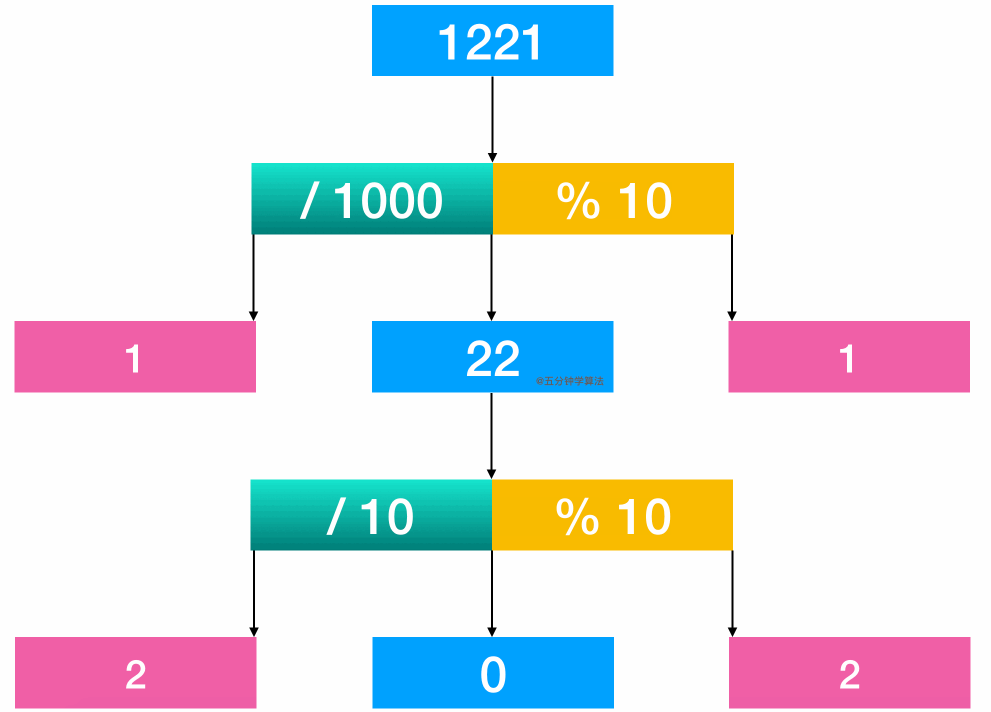
For example: the number 1221.

By calculating 1221 / 1000, the first 1 is obtained
By calculating 1221% 10, the last 1 can be obtained
Compare
Then take out 22 and continue to compare

code implementation

 public boolean isPalindrome(int x) {
 	//Boundary judgment
        if(x < 0)return false;
        int div = 1;
        while(x / div >= 10) div *= 10;
        while(x > 0){
            int left = x / div;
            int right = x % 10;
            if(left != right) return false;
            x = (x % div)/10;
            div /= 100;
        }
        return  true;
}

results of enforcement

From the results, the execution time is faster than the java solution, and the memory consumption is less than the java solution.

Advanced solution II: ingenious solution

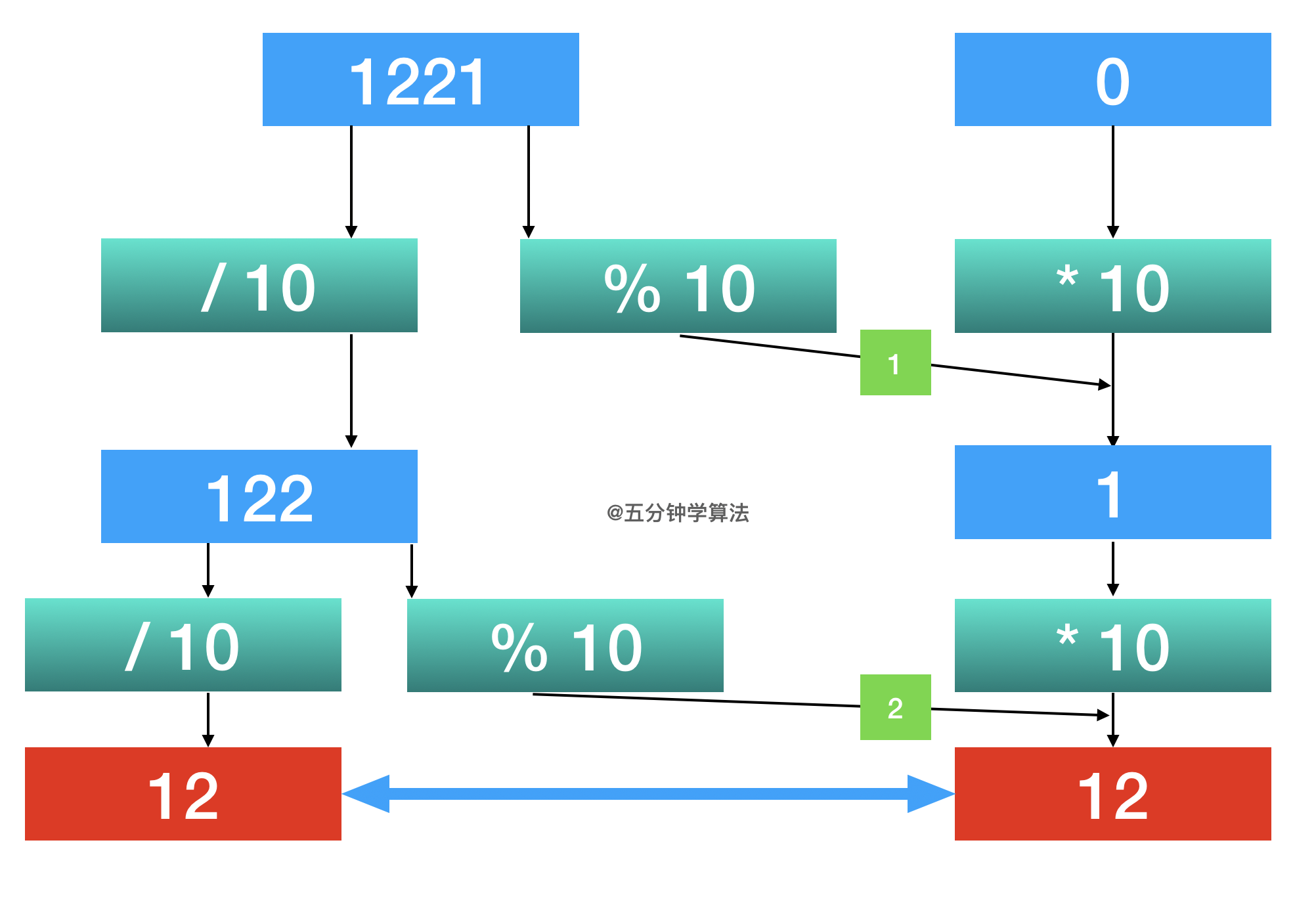
If you look at the palindrome number intuitively, it feels like folding the numbers in half to see whether they can correspond one by one.

Therefore, the operation of this solution is to take out the second half of the number and flip it.

One thing to note here is that the number of palindromes can be odd or even, so when its length is even, it should be equal when folded in half; When its length is an odd number, after it is folded in half, one digit of its length needs to be removed (divided by 10 and rounded).

The specific methods are as follows:

Take out the lowest number for each remainder operation (% 10): y = x% 10
Add the lowest number to the end of the fetched number: revertNum = revertNum * 10 + y
For each lowest digit, x is divided by 10
Judge whether x is less than revertNum. When it is less than, it indicates that the number is half or more
Finally, judge the case of odd and even numbers: if it is even, revertNum and x are equal; If it is an odd number, the middle number is on the lowest bit of revertNum. After dividing it by 10, it should be equal to x.

 public boolean isPalindrome(int x) {
        //Think: why can 0 at the end directly return false
        //Answer: the first digit of the number is 0 and is not displayed, so the end array is 0 and returns false directly
        if( x < 0 || (x % 10 == 0 && x != 0))return false;
        int revertedNumber = 0;
        while(x > revertedNumber){
            revertedNumber = revertedNumber *10 + x % 10;
            x /= 10;
        }
        return x == revertedNumber || x == revertedNumber / 10;
    }

Original author: cxywushixiong
Link: https://leetcode-cn.com/problems/palindrome-number/solution/dong-hua-hui-wen-shu-de-san-chong-jie-fa-fa-jie-ch/
Source: LeetCode