Catalog

Definition

1. Conventional method judgment

2. The most effective way to judge

3 test

Definition

An integer whose divisor is only 1 and itself is called a prime number, or prime number.

1. Conventional method judgment

According to the definition, since prime numbers have no divisors other than 1 and itself, it is sufficient to judge whether n is prime or not, and directly judge whether there is a divisor of N from 2 to n-1 according to the definition.

The Java code is as follows:

 1 /**
 2      * The general method of judging whether it is prime or prime
 3      * Judge whether n is prime or not, and directly judge whether there is a divisor of N from 2 to n-1 according to the definition.
 4      * @param num
 5      * @return
 6      */
 7     public static boolean isPrimeNormal(int num) {
 8         for(int i=2; i<num; i++) {
 9             if(num%i == 0) {
10                 return false;
11             }
12         }
13         
14         return true;
15     }
16  

2. The most effective way to judge

First, let's look at a rule about the distribution of prime numbers: prime numbers greater than or equal to 5 must be adjacent to multiples of 6, such as 5 and 7, 11 and 13, 17 and 19, etc.

It is proved that if x ≥ 1, the natural number greater than or equal to 5 is expressed as follows:
······ 6x-1，6x，6x+1，6x+2，6x+3，6x+4，6x+5，6(x+1)，6(x+1)+1 ······

It can be seen that the numbers on both sides of the multiples of 6 are 6x+2, 6x+3, 6x+4, because 2(3x+1), 3(2x+1), 2(3x+2), they must not be prime numbers, and then remove 6x itself. Obviously, the prime numbers can only appear on the adjacent sides of 6x.

In addition, we know that if a number can be factorized, the two numbers obtained in the decomposition must be one less than or equal to sqrt(n), and one greater than or equal to sqrt(n). Therefore, it is not necessary to traverse n-1 in the above code, just to traverse sqrt(n), because if the left side of sqrt(n) cannot find the divisor, then the right side must not find the divisor.

The Java code is as follows:

 1 /**
 2      * The most effective way to judge whether it is prime or prime
 3      * 1.2 and 3 less than 5
 4      * 2.Prime numbers greater than or equal to 5 must be adjacent to multiples of 6, such as 5 and 7, 11 and 13, 17 and 19, and so on.
 5      * @param num
 6      * @return
 7      */
 8     public static boolean isPrime(int num) {
 9         //Two decimals to be treated separately 
10         if(num==2 || num==3) {
11             return true;
12         }
13         
14         //It must not be a prime number on both sides of a multiple of 6.
15         if(num%6!=1 && num%6!=5) {
16             return false;
17         }
18         
19         int tmp = (int) Math.sqrt(num);//Get square root
20         //On either side of a multiple of 6 may not be a prime
21         for(int i=5; i<=tmp; i+=6) {
22             if(num%i==0 || num%(i+2)==0) {
23                 return false;
24             }
25         }
26         
27         return true;
28     }

Let's look at the performance test of these two methods:

 1 public static void main(String[] args) {
 2         int testNum = 1000000;
 3         
 4         //Routine method test
 5         long start1 = Calendar.getInstance().getTimeInMillis();
 6         for(int i=0; i<testNum; i++) {
 7             isPrimeNormal(i);
 8         }
 9         long end1 = Calendar.getInstance().getTimeInMillis();
10         System.out.println("Conventional method, consumption time(ms):" + (end1 - start1));
11         
12         //Most effective method test
13         long start2 = Calendar.getInstance().getTimeInMillis();
14         for(int i=0; i<testNum; i++) {
15             isPrime(i);
16         }
17         long end2 = Calendar.getInstance().getTimeInMillis();
18         System.out.println("Most effective method, consumption time(ms):" + (end2 - start2));
19     }

3 test

The test results are as follows:

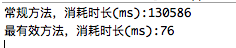
Finally, it is noted that the idea of this algorithm comes from: https://blog.csdn.net/huang_miao_xin/article/details/51331710

https://blog.csdn.net/qq_15092079/article/details/80804326