Before the formal circular queue learning, let's take a look at the problem of deleting the queue head element in the sequential queue:

(1) Let's set an array with capacity=8 and size=5(a,b,c,d,e). The left side is the team head and the right side is the team tail.

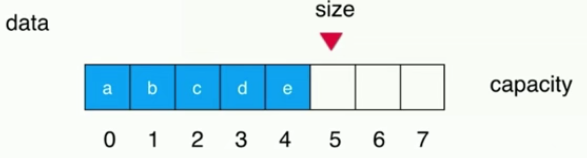
(2) After an element is out of the team, it needs to move forward one bit as a whole

Team:

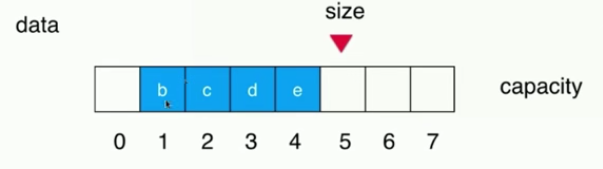
Move the whole forward one bit:

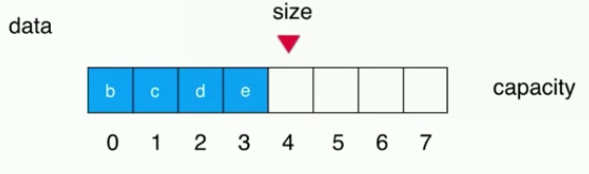
It is easy to get that the time complexity is O(n).

At this time, we want to know whether we can record who the front of the team is in the array instead of moving the whole element forward, and the tail of the team points to the position when the next element enters the team, so that when there is another team, we only need to maintain the direction of the front without moving the element. So we have a circular queue.

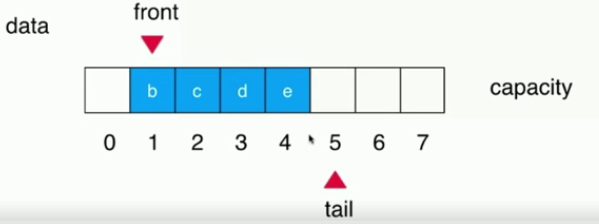
1. Principle of circular queue

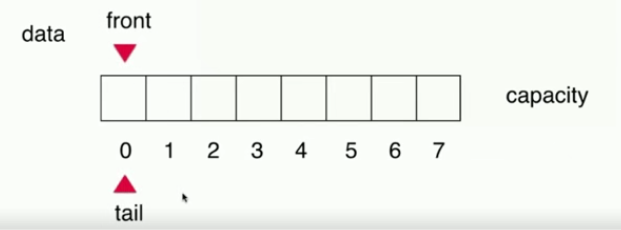
(1) Initially, when the whole array is empty, the queue is empty when the front and tail of the queue point to the same position (where the array index is 0), that is, when the front==tail

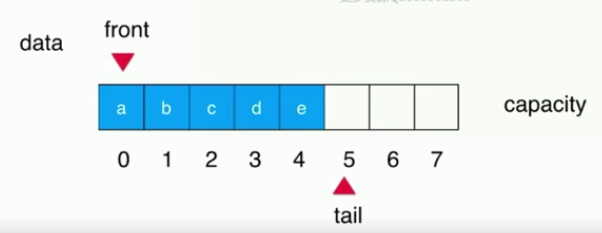
(2) When you add elements to an array

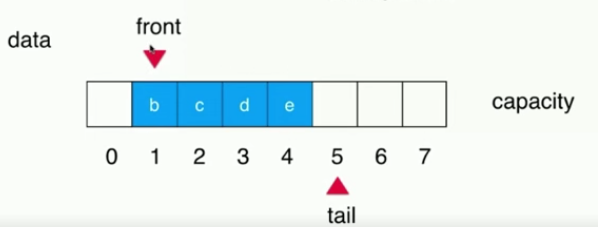
(3) Queue an element, front points to a new location

(4) Team entry element, tail overlay

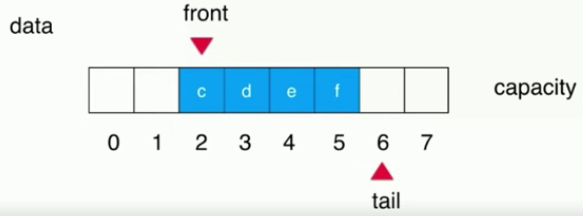
(5) When the tail cannot be increased, there is still space in front of the array. At this time, the loop queue will appear.

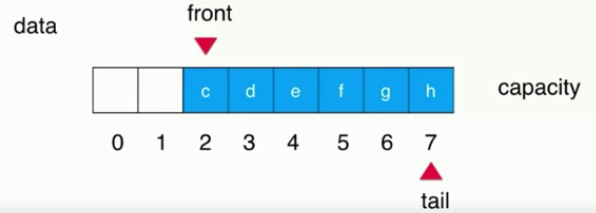
At this point, the array should change to this:

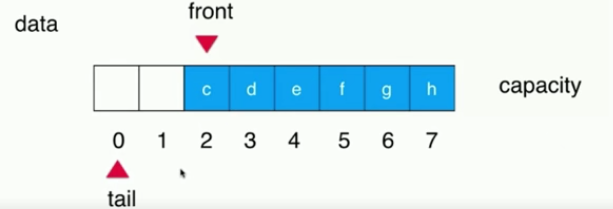
Add an element to the array:

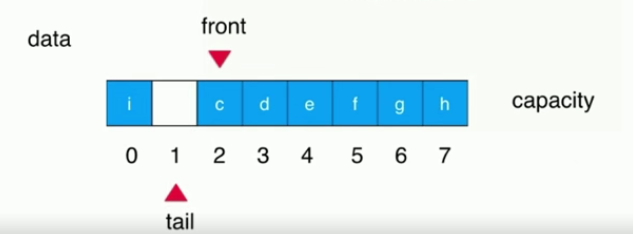
In this way, the array is full (tail+1==front queue is full), and the expansion operation starts. In capacity, a space is wasted.

In order to return the tail to the front of the array, change the queue full expression to (tail+1)% c==front so that the array can move in a circular way.

2. Implementation of cyclic queue code

Create a new class LoopQueue and implement the interface Queue.

2.1. The interface Queue code is as follows:

package Queue;
 
public interface Queue<E> {
//Get the number of elements in the queue
int getSize();
 
//Whether the element in the queue is empty
boolean isEmpty();
 
//Queue entry
void enqueue(E e);
 
//Outgoing queue
E dequeue();
 
//Get team leader element
E getFront();
}

2.2. Relevant codes of LoopQueue:

package Queue;
 
//Circular queue
public class LoopQueue<E> implements Queue<E> {
private E[] data;
private int front, tail;
private int size;//Number of elements in the queue
 
//Constructor, capacity constructor for incoming queues
public LoopQueue(int capacity) {
data = (E[]) new Object[capacity + 1];//Waste and a space
front = 0;
tail = 0;
size = 0;
}
 
//Parameterless constructor, capacity of default queue capacity=10
public LoopQueue() {
this(10);
}
 
//True capacity
public int getCapacity() {
return data.length - 1;
}
 
//Whether the queue is empty
@Override
public boolean isEmpty() {
return front == tail;
}
 
//Number of elements in the queue
@Override
public int getSize() {
return size;
}
 
//Incoming operation
@Override
public void enqueue(E e) {
if ((tail + 1) % data.length == front) {//The queue is full and needs to be expanded
resize(getCapacity() * 2);
}
data[tail] = e;
tail = (tail + 1) % data.length;
size++;
}
 
//Team operation
 
@Override
public E dequeue() {
if (isEmpty()) {
throw new IllegalArgumentException("Queue is empty");
}
 
E ret = data[front];
data[front] = null;//Manual release
front = (front + 1) % data.length;
size--;
if (size == getCapacity() / 4 && getCapacity() / 2 != 0) {
resize(getCapacity() / 2);
}
return ret;
}
 
//Get team leader element
@Override
public E getFront() {
if (isEmpty()) {
throw new IllegalArgumentException("Queue is empty");
}
return data[front];
}
 
//Changing capacity
private void resize(int newCapacity) {
E[] newData = (E[]) new Object[newCapacity + 1];
for (int i = 0; i < size; i++) {
newData[i] = data[(front + i) % data.length];//Loop array to prevent out of bounds
}
data = newData;
front = 0;
tail = size;
}
 
 
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append(String.format("Queue:size=%d, capacity=%d\n", size, getCapacity()));
res.append("front [");
for (int i = front; i != tail; i = (i + 1) % data.length) {
res.append(data[i]);
if ((i + 1) % data.length != tail) {
res.append(",");
}
}
res.append("] tail");
return res.toString();
}
 
 
 
}

In the LoopQueue class, you need to pay attention to:

(1) In line 11, the + 1 is that capacity needs to waste a space, so in the instantiation, add 1 more

data = (E[]) new Object[capacity + 1];//Waste and a space

(2) The real capacity of the 24 rows is data.length-1, because there is a waste of space.

data.length - 1;

(3) About the tail value of the 46th line in the team

In order to ensure that the entry is a cyclic operation, the change rule of tail value is

tail = (tail + 1) % data.length;

(4) For the data migration operation of line 82, the remainder operation is to prevent the array from being out of bounds.

newData[i] = data[(front + i) % data.length];//Loop array to prevent out of bounds

2.3. Directly add a main function to LoopQueue for testing. The relevant codes are as follows:

//test case
public static void main(String[] args) {
LoopQueue<Integer> queue = new LoopQueue<Integer>();
for (int i = 0; i < 10; i++) {
queue.enqueue(i);
System.out.println(queue);
 
if(i%3==2){//One for every 3 elements added
queue.dequeue();
System.out.println(queue);
}
 
}
 
}

The result is:

3. Cycle queue time complexity

At this point, we have implemented a circular queue operation, which solves the problem of O(n) time complexity when queuing out in the sequence queue, and O(1) time complexity when queuing out in the circular queue.