preface

Today, I took part in a written test and came up with this question. I didn't do it in the end. It's a real dish. After the written examination, I thought again and finally realized the requirements of the topic

subject

The requirements of the topic are as follows (I can't remember):

1. First enter an integer n, the range seems to be [0, 10], so the specification of the matrix is n * n;
2. Enter n integers in each line, that is, enter a matrix;
3. Then enter an integer m, which is the number of clockwise rotations of the matrix. There is also a range. Forget, it doesn't matter;

sample input

3
1 2 3
4 5 6
7 8 9
4

sample output

9 8 7
6 5 4
3 2 1

thinking

There are so many requirements for the topic. My main idea is to do a rotation first, and then directly package it into a method and put it in m cycles. As a result, my brain was so simple and cracked at the time of my written test. Let's take a look at it step by step
The first is the basic framework of the main function:

public class Test {
	public static void main(String[] args) {
		Scanner input = new Scanner(System.in);
		//Enter integer n
		int n = input.nextInt();
		int[][] arr = new int[n][n];
		//Input matrix
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				arr[i][j] = input.nextInt();
			}
		}
		//Enter m
		int m = input.nextInt();
		//Rotate m times
		for (int i = 0; i < m; i++) {
			 //Call the method to rotate once
			 arr = RotateArray(arr, n);
		}
		//ergodic matrix 
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				System.out.print(arr[i][j] + " ");
			}
			System.out.println();
		}
	}
}

Then there is the rotation method:
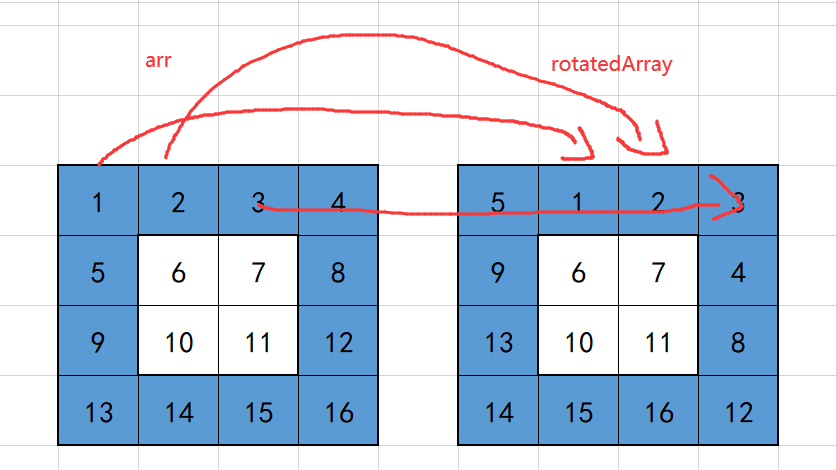
The idea is to import the original matrix and create a new matrix with the same specification to store the rotated data
Divide a large matrix into multiple rings, rotate one ring at a time, and then narrow the range and continue to rotate
No, I don't know how to explain it. Why don't you post a code first

//Because you are too lazy to new an object, you can directly modify it to static
public static int[][] RotateArray(int[][] arr, int n) {
	int i = 0, int j = 0; //Old matrix start position
	int left = 0, rigth = n, up = 0, down = n;//Specify current scope
	int[][] rotatedArray = new int[n][n];//Create a new matrix with the same specifications
	//You'd better Debug the process yourself. It may be more clear, that is, draw a circle, turn one layer and continue to turn the next layer until all are turned
	while (left < rigth-1) {
		while (j+1 < rigth) {
			rotatedArray[i][j+1] = arr[i][j];
			j++;
		}
		while (i+1 < down) {
			rotatedArray[i+1][j] = arr[i][j];
			i++;
		}
		while (j > left) {
			rotatedArray[i][j-1] = arr[i][j];
			j--;
		}
		while (i > up) {
			rotatedArray[i-1][j] = arr[i][j];
			i--;
		}
		//Next initial position
		i++;
		j++;
		//Narrow the matrix
		left++;
		rigth--;
		up++;
		down--;
		//This is the case where only the most central element is left
		if (left == rigth-1) {
			rotatedArray[up][left] = arr[up][left];
		}
	}
	//Returns the matrix after one rotation
	return rotatedArray;
}

Similarly, white is the rotating part of the next cycle

ending

OK, that's it. I didn't feel very good when I wrote this algorithmic blog for the first time. Please forgive me. I don't know what better way to do. If a little partner knows it, he can comment or recommend it to me in a private letter. If he doesn't understand it, he can also comment or ask directly in a private letter

Complete code

public class Test {
	public static void main(String[] args) {
		Scanner input = new Scanner(System.in);
		int n = input.nextInt();
		int[][] arr = new int[n][n];
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				arr[i][j] = input.nextInt();
			}
		}
		int m = input.nextInt();

		for (int i = 0; i < m; i++) {
			 arr = RotateArray(arr, n);
		}
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				System.out.print(arr[i][j] + " ");
			}
			System.out.println();
		}
	}
	public static int[][] RotateArray(int[][] arr, int n) {
		int i = 0;
		int j = 0;
		int left = 0, rigth = n, up = 0, down = n;
		int[][] rotatedArray = new int[n][n];
		while (left < rigth-1) {
			while (j+1 < rigth) {
				rotatedArray[i][j+1] = arr[i][j];
				j++;
			}
			while (i+1 < down) {
				rotatedArray[i+1][j] = arr[i][j];
				i++;
			}
			while (j > left) {
				rotatedArray[i][j-1] = arr[i][j];
				j--;
			}
			while (i > up) {
				rotatedArray[i-1][j] = arr[i][j];
				i--;
			}
			i++;
			j++;
			left++;
			rigth--;
			up++;
			down--;
			if (left == rigth-1) {
				rotatedArray[up][left] = arr[up][left];
			}
		}
		return rotatedArray;
	}
}