Photogrammetry programming 1 - space resection

A file needs to be created for the required data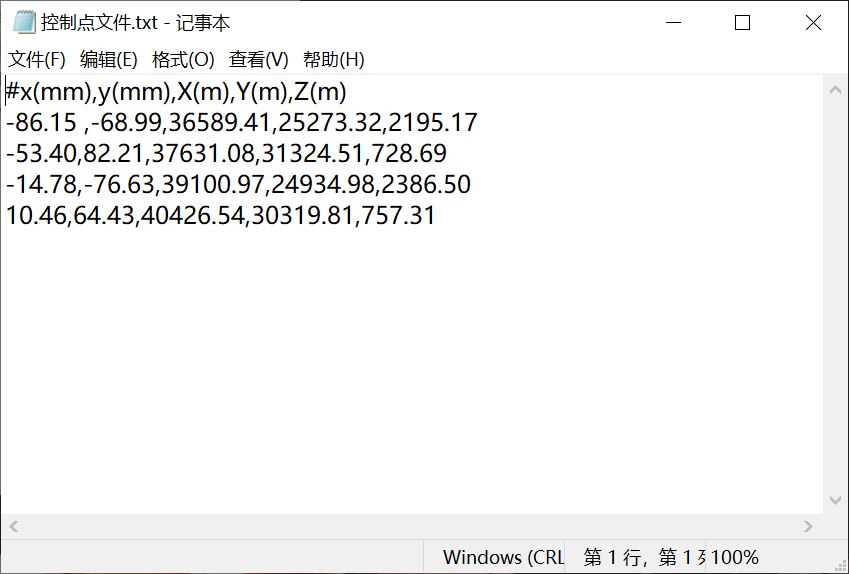

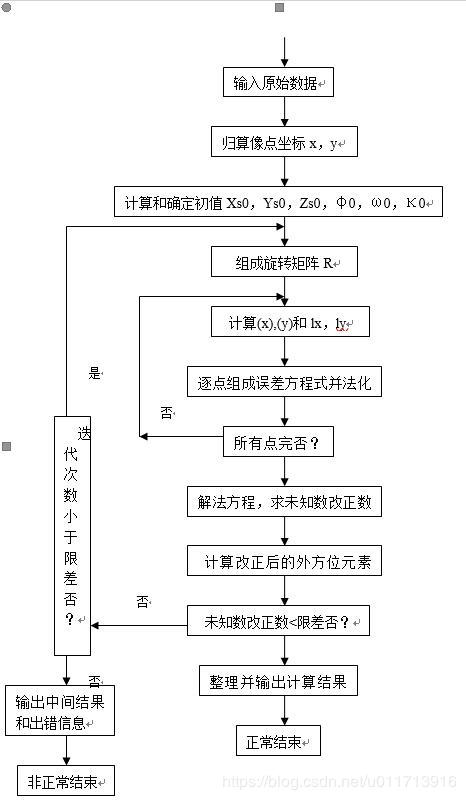
1) Obtain known data. The average altitude and the main distance of the camera are obtained from the aerial photogrammetry data, and the ground measurement coordinates of the control points are obtained and converted into the ground photogrammetry coordinates.

(2) Measure the coordinates of control points and make system correction.

(3) Determine the initial value of the unknown. In the case of vertical photography and roughly uniform distribution of ground control points, determine the initial value as follows: q=w=k=0, where m is the scale denominator of photography and n is the number of control points.

(4) Using the initial values of three corner elements, the cosine of each direction is calculated to form the rotation matrix R.

(5) Calculate the approximate value of image point coordinate point by point. Using the approximate value of the unknown number and the ground coordinate of the control point to substitute the collinear equation, the approximate value (x) and (y) of the image point coordinate are calculated point by point.

(6) The coefficient and constant term of the error equation are calculated point by point to form the error equation.

(7) The coefficient matrix A and the constant term L of the normal equation are calculated to form the normal equation.

(8) By solving the equation, the correction numbers dXs, dYs, dZs, dq, dw, dk of the elements of the exterior orientation are obtained.

(9) The new value of the exterior orientation element is calculated by using the approximate value obtained in the previous iteration and the correction number of this iteration.

(10) Compare the correction number of the exterior orientation element with the specified limit difference. If it is less than the limit difference, the iteration ends. Otherwise, use a new one

Repeat (4) - (9) until the requirements are met

Insert a code slice here
import numpy as sy
from math import *
import tkinter as tk
import easygui as g
import tkinter.filedialog
import tkinter.messagebox as tm
from tkinter import messagebox
g.msgbox('Open file',ok_button = 'Select file')
path = tk.filedialog.askopenfilename()#Read file path
test=sy.loadtxt(path,delimiter=',',skiprows=0)#Read file data
print(len(test))
print('The raw data are as follows((x,y),(X,Y,Z)):\n',test)
m=eval(input('Please enter the scale bar( m): '))
f=eval(input('Please enter the main distance( m): '))
x0,y0=0,0
xy=[]
XYZ=[]
num=0
for i in range(len(test)):
    xy.append([test[i][0]/1000,test[i][1]/1000])
#Divided by 1000 because of uniform units
    XYZ.append([test[i][2],test[i][3],test[i][4]])
#Respectively form the matrix of image point control points
A=sy.mat(sy.zeros((8,6)))
#Four control points, each with 2 rows and 6 columns, four control points with 8 rows and 6 columns
#v=ax-l
#mat function is used to convert a list into a corresponding matrix. Zeros function is used to generate all zeros of a specified dimension. It has two contents
L=sy.mat(sy.zeros((8,1)))
R=sy.mat(sy.zeros((3,3)))
pds=sy.mat(sy.zeros((4,3)))
XS0=0
YS0=0
#Rotation matrix
for i in range(len(test)):
    XS0=(test[i][2]+XS0)/4
    YS0=(test[i][3]+YS0)/4
    ZS0=m*f
print('The initial coordinates of the line elements are as follows(XS0,YS0,ZS0):\n')
print(XS0)
print(YS0)
print(ZS0)
#Xs0=sumxti/t is the initial value
pi=0
w=0
k=0
diedai=0
while(True): 
	a1 = cos(pi)*cos(k)-sin(pi)*sin(w)*sin(k)
	a2 = (-1.0) * cos(pi) * sin(k) - sin(pi) * sin(w) * cos(k)
        a3 = (-1.0) * sin(pi) * cos(w)
        b1 = cos(w) * sin(k)
        b2 = cos(w) * cos(k)
        b3 = (-1.0) * sin(w)
        c1 = sin(pi) * cos(k) + cos(pi) * sin(w) * sin(k)
        c2 = (-1.0) * sin(pi) * sin(k) + cos(pi) * sin(w) * cos(k)
        c3 = cos(pi) * cos(w)
        R=sy.mat([[a1,a2,a3],[b1,b2,b3],[c1,c2,c3]])
 #The fourth step is to calculate the rotation matrix RA[i * 2,0] = (-1.0) * f / (ZS0)
	for i in range(0,len(XYZ)):

        	x = xy[i][0]
       		y = xy[i][1]
        	Xp = a1*(XYZ[i][0]-XS0) + b1*(XYZ[i][1]-YS0) + c1*(XYZ[i][2]-ZS0);
        	Yp = a2*(XYZ[i][0]-XS0) + b2*(XYZ[i][1]-YS0) + c2*(XYZ[i][2]-ZS0);
        	Zp = a3*(XYZ[i][0]-XS0) + b3*(XYZ[i][1]-YS0) + c3*(XYZ[i][2]-ZS0);
 #Finding the mean
        	A[2*i, 0] = (a1*f + a3*(x-x0))/Zp
        	A[2*i, 1] = (b1*f + b3*(x-x0))/Zp
        	A[2*i, 2] = (c1*f + c3*(x-x0))/Zp
        	A[2*i, 3] = (y-y0)*sin(w)-(((x-x0)*((x-x0)*cos(k) - (y-y0)*sin(k)))/f+ f*cos(k))*cos(w);
        	A[2*i, 4] = -f*sin(k) - (x-x0)*((x-x0)*sin(k) +(y-y0))*cos(k)/ f
        	A[2*i, 5] = y-y0;
        	A[2*i+1, 0] = (a2*f + a3*(y-y0)) / Zp
        	A[2 * i + 1, 1] = (b2*f + b3*(x-x0))/ Zp 
        	A[2 * i + 1, 2] = (c2*f + c3*(x-x0))/Zp
        	A[2 * i + 1, 3] = -(x-x0)*sin(w) - ((y-y0)*(x*cos(k) - y)*sin(k)) / f - f*sin(k)*cos(w);
        	A[2 * i + 1, 4] = -f*cos(k) - (y-y0)/ f*((x-x0)*sin(k) + (y-y0)*cos(k))
        	A[2 * i + 1, 5] = -(x-x0)
        #a11 equal coefficient ''
       		L[i * 2,0]=x+f*(Xp/Zp)
        	L[i * 2 + 1,0] =y+f*(Yp/Zp)
        #Constant term l
    Result = [0]*(9+4)
#Saving and correcting
    Result=((A.T*A).I)*A.T*L
    XS0+=Result[0]
    YS0+=Result[1]
    ZS0+=Result[2]
    pi+=Result[3]
    w+=Result[4]
    k+=Result[5]
    diedai=diedai+1
    if (fabs (Result[3]) < 1e-6) and (fabs (Result[4]) < 1e-6) and (fabs (Result[5]) < 1e-6):
        break
    if diedai >60:
        print("Error:overtime")
        break
a1=cos(pi)*cos(k)-sin(pi)*sin(w)*sin(k)
a2=(-1.0) * cos(pi) * sin(k) - sin(pi) * sin(w) * cos(k)
a3=(-1.0) * sin(pi) * cos(w)
b1=cos(w) * sin(k)
b2=cos(w) * cos(k)
b3=(-1.0) * sin(w)
c1=sin(pi) * cos(k) + cos(pi) * sin(w) * sin(k)
c2=(-1.0) * sin(pi) * sin(k) + cos(pi) * sin(w) * cos(k)
c3=cos(pi) * cos(w)
rotate=sy.mat([[a1,a2,a3],[b1,b2,b3],[c1,c2,c3]])
list1=["XS0:",XS0,"YS0:",YS0,"ZS0:",ZS0,"pi:",pi,"w:",w,"k:",k]
print('Calculation results\n','Exterior orientation elements:\n:'"XS0:",XS0,'\n',"YS0:",YS0,'\n',"ZS0:",ZS0,'\n','PI:',pi,'\n','W:',w,'\n',"K:",k,'\n')
print('Rotation matrix\n',rotate)
print('The number of iterations is:',diedai)
messagebox.showinfo("The exterior azimuth element is:",list1)