Occasionally, I saw such a story in Mr. Wu Jun's top of the wave (Fourth Edition).

Google once advertised on the 101 highway in California with a large billboard:

{the first ten consecutive prime numbers in irrational number e} com

If you know the answer (7427466391.com), you can enter Google's recruitment website through the above website. And it's smart to be able to work out this problem.

"Very smart"? Mr. Wu Jun's words are interesting. He also tried to figure out the proof with the help of the power of the computer.

thinking

As we all know, e is an irrational number, in other words, infinite non cyclic decimal. There are always some math lovers in the world who enjoy using computers to calculate the decimal places of these irrational numbers, π, e is no exception. So,

The first step is to find the decimal data of E on some authoritative mathematical websites;

At this time, it's Google Dafa. It's coming to E Wikipedia English Encyclopedia On the page, I noticed the "A001113" hyperlink behind the decimal expression below e, so I clicked in to have a look.

Then came the of the OEIS site A001113 page It turned out to be a very authoritative database website in number theory.

With the eyes of treasure hunting, I scanned the web page up and down, left and right, and finally found the target. The first entry in LINKS is.

N. J. A. Sloane, Table of 50000 digits of e labeled from 1 to 50000 [based on the ICON Project link below]

The author is also N.J.A Sloane who founded the OEIS organization. It seems that he is a big man in this field. I'm sorry that he doesn't know Taishan.

Click in this Table of 50000 digits of e labeled from 1 to 50000 , the results of the page are very pleasant. Direct plain text data. The left column is the decimal places and the right column is the corresponding value. When we get the data, we can carry out the follow-up work after simple processing. I hope the answer to this proof question is in the number of 50000, otherwise we have to expand the scope.

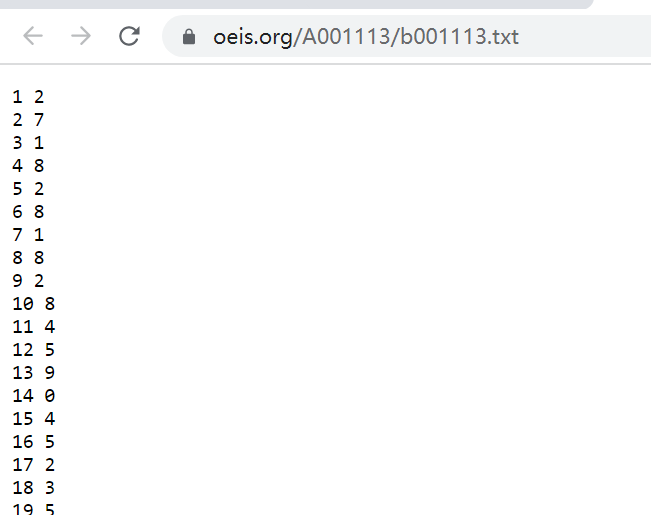
At this point, with the decimal data of e irrational numbers, you can start the next step.

The second step, how to judge whether a number is prime?

Since primary school, mathematics teachers have taught us that the definition of prime number refers to a natural number greater than 1 that cannot be divided by other natural numbers except 1 and the number itself. Therefore, the natural judgment idea is to judge whether 2 → n can divide n for a natural number n greater than 1. If it is found that a number can divide n, then n is not a prime number, otherwise it is. In addition, considering the symmetry, we do not have to increase to N. for example, for 2 * 3 and 3 * 2, 6 / 2 and 6 / 3 are judged as composite numbers, but it is sufficient to increase to 2, so we do not need to consider 3.

Python code is as follows:

def isPrime(n: int) -> bool:
  if n <= 1:
    return False
  i = 2
  # Make use of symmetry. For example, 2*3=6, 3*2=6
  while i * i < n:
    if n % i == 0:
      return False
    i += 1
  return True

When looking up the information related to prime numbers on the Internet, I found that there is a law of prime number distribution in number theory, which can also be used to judge prime numbers. Source—— Prime decision algorithm

Distribution law of prime numbers:

When n > = 5, if n is a prime number, then n% 6 = 1 | n% 6 = 5, that is, n must appear on both sides of 6x (x ≥ 1). In other words, any prime number can be expressed as 6x ± 1, X ∈ n.

prove:

The number near 6x is expressed as follows:

......(6x - 1), 6x, 6x + 1, 2(3x + 1), 3(2x + 1), 2(3x + 2), 6x + 5, 6(x+1)......

The numbers not on both sides of 6x are: 2(3x + 1), 3(2x + 1), 2(3x + 2). They are not prime numbers, so prime numbers appear on both sides of 6x.

The following is implemented in Python code. The time complexity is almost the same as that of the previous one, but it is enough for our proof.

def isPrime(n: int) -> bool:
  if n <= 1:
    return False
  if n <= 3:
    return True
  # For case of 2(3x + 1), 3(2x + 1), 2(3x + 2)
  if n % 2 == 0 or n % 3 == 0:
    return False
  # For case of the multiplication of prime numbers
  i = 5
  while i * i < n:
    if n % i == 0 or n % (i + 2) == 0:
      return False
    i += 6
  return True

In addition, it is of great use to determine prime numbers in cryptography, such as the famous RSA algorithm. In terms of judging the prime number algorithm, the above simple remainder algorithm with high time complexity is not adopted, but Fermat's small theorem, Miller Rabin algorithm and solovay Strassen algorithm, which are difficult to understand. For details, please refer to this article—— PyCrypto cryptography library source code analysis (I) generation of random numbers and large prime numbers , and the one above.

At this point, the necessary materials are ready for the last step.

In the third step, the decimal data of for loop e determines the first 10 bit prime number.

To get straight to the point, throw out the source code first.

Specific idea: first use the requests library to obtain the e decimal data, and then transfer it to a file for line by line reading. The for loop reads each decimal data line by line, performs slicing operation, arranges it into 10 bit integers required for proof, and obtains an ordered list with a total number of 49991. Then use the prime number determination function to determine these 10 bit integers one by one, and finally get the answer - 7427466391.

import requests
import re

response = requests.get('https://oeis.org/A001113/b001113.txt')

# Save sequence to a file for later use
out_file = open('digits_of_e.txt', 'w')
print(response.text, file=out_file)

queue = []

container = ''
counter = 0  
in_file = open('digits_of_e.txt', 'r')
list_in_file = list(in_file)
for index, line in enumerate(list_in_file):
  segments = list_in_file[index:index+10]
  # get lines at a batch of 10 lines
  for segment in segments:
    matchObj = re.match(r'([\d]*) (\d).*', segment, re.I)
    counter += 1
    if counter <= 10:
      container += matchObj.group(2) if matchObj != None else ''
    else:
      counter = 1
      if len(container) == 10:
        queue.append(container)
      container = matchObj.group(2) if matchObj != None else ''
in_file.close()

print(len(queue)) # 49991 indeed

def isPrime(n: int) -> bool:
  # Prime number definition version:
  '''
  if n <= 1:
    return False
  i = 2
  # Make use of symmetry. For example, 2*3=6, 3*2=6
  while i * i < n:
    if n % i == 0:
      return False
    i += 1
  return True
  '''
  # Distribution pattern of prime number version:
  if n <= 1:
    return False
  if n <= 3:
    return True
  # For case of 2(3x + 1), 3(2x + 1), 2(3x + 2)
  if n % 2 == 0 or n % 3 == 0:
    return False
  # For case of the multiplication of prime numbers
  i = 5
  while i * i < n:
    if n % i == 0 or n % (i + 2) == 0:
      return False
    i += 6
  return True

result = None
for num in queue:
  if isPrime(int(num)):
    print(num)
    result = num
    break

print(result == '7427466391')
print(isPrime(7427466391))

Operation results:

Bingo!

end

After the proof problem is solved, I have to take a sense of ceremony and visit this website - 7427466391 com.

The result is 502 error

OK, it seems that this site has long been abandoned by others. After all, this highway advertisement was also a prank played by Google in 2004.

Finally, the source code is sorted into a Kaggle Notebook version. Welcome to check!

First10DigitPrimeFoundInConsecutiveDigitsOfE | Kaggle

Reference summary

1. Wu Jun's top of the wave (Fourth Edition) P44
2. Of irrational number e Wikipedia English Encyclopedia
3. Of OEIS sites A001113 page
4. Table of 50000 digits of e labeled from 1 to 50000
5. Prime decision algorithm
6. PyCrypto cryptography library source code analysis (I) generation of random numbers and large prime numbers
7. What Google's Genius Billboard From 2004 Can Teach Us About Solving Problems