1. Sword finger Offer 32 - I. print binary tree from top to bottom
Sword finger Offer 32 - I. print binary tree from top to bottom
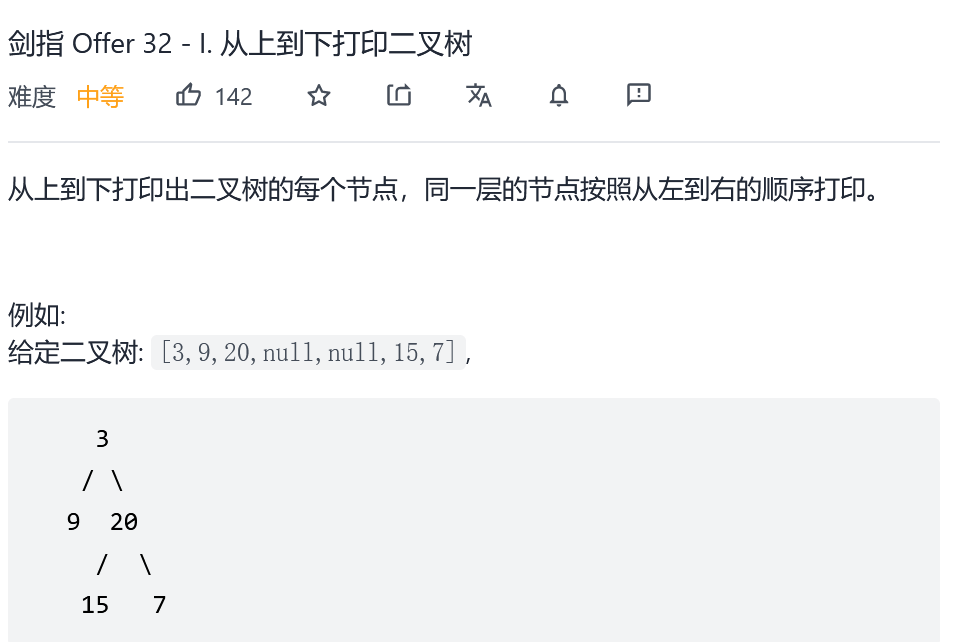
Idea: use the queue to traverse the hierarchy
class Solution {
public int[] levelOrder(TreeNode root) {
if(root==null)
return new int[0];//When root is null, return []
ArrayList<Integer> list=new ArrayList<>();
LinkedList<TreeNode> q=new LinkedList<>();
q.offer(root);
while(!q.isEmpty())
{
TreeNode node=q.pop();
list.add(node.val);
if(node.left!=null)
q.add(node.left);
if(node.right!=null)
q.add(node.right);
}
int ans[]=new int[list.size()];
for(int i=0;i<list.size();i++)
{
ans[i]=list.get(i);
}
return ans;
}
}
//O (n) BFS needs N cycles
//O(n/2) when the number is a balanced binary tree, there are at most n/2 nodes in the queue
2. Sword finger Offer 32 - II. Print binary tree from top to bottom II
Sword finger Offer 32 - II. Print binary tree II from top to bottom
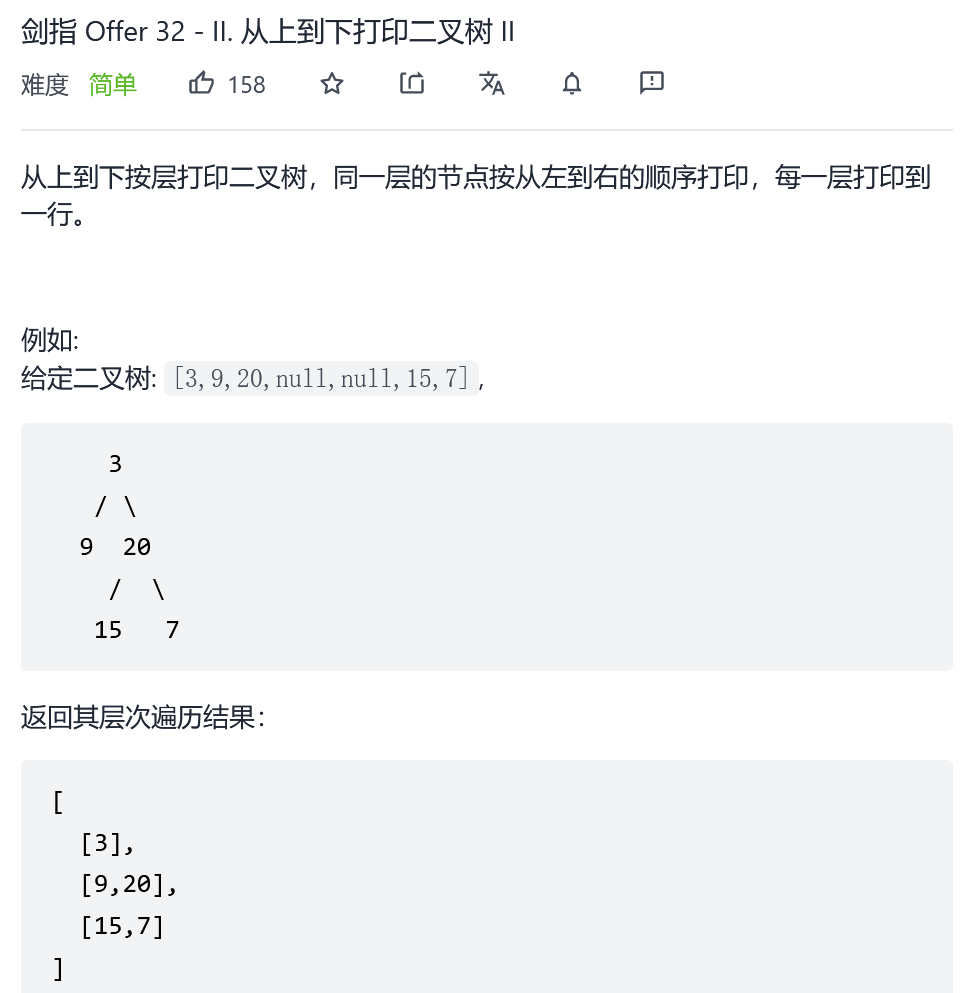
Idea: use the queue to traverse the hierarchy, but you need to record the nodes of each layer as a list, that is, you need to traverse each layer separately internally
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> list=new ArrayList<>();
if(root==null)
return list;
LinkedList<TreeNode> q=new LinkedList<>();
q.offer(root);
while(!q.isEmpty())
{
int size=q.size();
List<Integer> level=new ArrayList<>();
for(int i=0;i<size;i++)//Traverse each layer
{
TreeNode node=q.pop();
level.add(node.val);
if(node.left!=null)
q.offer(node.left);
if(node.right!=null)
q.offer(node.right);
}
list.add(level);
}
return list;
}
}
//O (n) BFS needs N cycles
//O(n/2) when the number is a balanced binary tree, there are at most n/2 nodes in the queue
3. Sword finger Offer 32 - III. print binary tree III from top to bottom
Sword finger Offer 32 - III. print binary tree III from top to bottom

Idea: use the queue to traverse the hierarchy. The order of adding each layer is different. The first layer is added from left to right, and the second column is added from right to left... You can set a layer number. Odd layers are added in positive order and even columns are added in reverse order
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> list=new ArrayList<>();
if(root==null)
return list;
LinkedList<TreeNode> q=new LinkedList<>();
q.offer(root);
int levelNum=1;//The layer number is initialized to 1
while(!q.isEmpty())
{
int size=q.size();
//LinkedList is used here to add nodes upside down
LinkedList<Integer> level=new LinkedList<>();
for(int i=0;i<size;i++)//Traverse each layer
{
TreeNode node=q.pop();
if(levelNum%2!=0)//Add odd layers
level.addLast(node.val);
else//Even layers added upside down
level.addFirst(node.val);
if(node.left!=null)
q.offer(node.left);
if(node.right!=null)
q.offer(node.right);
}
list.add(level);
levelNum++;
}
return list;
}
}
4. Sword finger Offer 26. Substructure of tree
Sword finger Offer 26. Substructure of tree

Idea: traverse each node a of tree a, and then judge whether there is a subtree with a as the root node. If it is the same as B, it will return true. Otherwise, continue to judge. The distribution will start with the left child node and the right child node of A. if tree a has not returned true after traversing, it indicates that B is not a subtree of A; In the process of comparison, if tree B has not returned false after traversing, it means that B is a subtree of A. two functions are required, one is substructure() for deep traversal, and the other is judge to judge whether the subtree starting from the current node is the same as B
class Solution {
public boolean isSubStructure(TreeNode A, TreeNode B) {
//false is returned whenever one of the trees is null
if(A==null||B==null)
return false;
//The following are not three judge s, because what you need is a preorder traversal (dfs), if
//If there is no substructure at the beginning of the current node, the next time starts with the left child of the current node
//Compare again, and then the left child node
return judge(A,B)||isSubStructure(A.left,B)||isSubStructure(A.right,B);
}
boolean judge(TreeNode A,TreeNode B)
{
if(B==null)//After traversing the B tree, false is not returned, indicating that it is true. First judge whether the B tree has been traversed
return true;
if(A==null)//Tree A is traversed, but tree B is not traversed
return false;
if(A.val!=B.val)//The current nodes are not equal
return false;
//The current node is equal, and then the values of the left child node and the right child node are compared
return judge(A.left,B.left)&&judge(A.right,B.right);
}
}
//O(MN) M is the number of nodes of A and N is the number of nodes of B. traversing A requires O(M). For each node of A, it needs to call recur and use O(N)
//O(M)
5. Sword finger Offer 27. Image of binary tree
Sword finger Offer 27. Image of binary tree

Idea 1: use recursive depth search to exchange nodes from bottom to top
class Solution {
public TreeNode mirrorTree(TreeNode root) {
if(root==null)
return null;
TreeNode tmp=root.left;
root.left=mirrorTree(root.right);
root.right=mirrorTree(tmp);
return root;
}
}
//O(N)
//O(N)
Idea 2: use auxiliary queue level traversal to exchange nodes from top to bottom
class Solution {
public TreeNode mirrorTree(TreeNode root) {
if(root==null)
return null;
LinkedList<TreeNode> q=new LinkedList<>();
q.offer(root);
while(!q.isEmpty())
{
TreeNode node=q.pop();
if(node.left!=null)
q.offer(node.left);
if(node.right!=null)
q.offer(node.right);
TreeNode tmp=node.left;
node.left=node.right;
node.right=tmp;
}
return root;
}
}
//O(N)
//O(N)
6. Sword finger Offer 28. Symmetric binary tree
Sword finger Offer 28. Symmetric binary tree
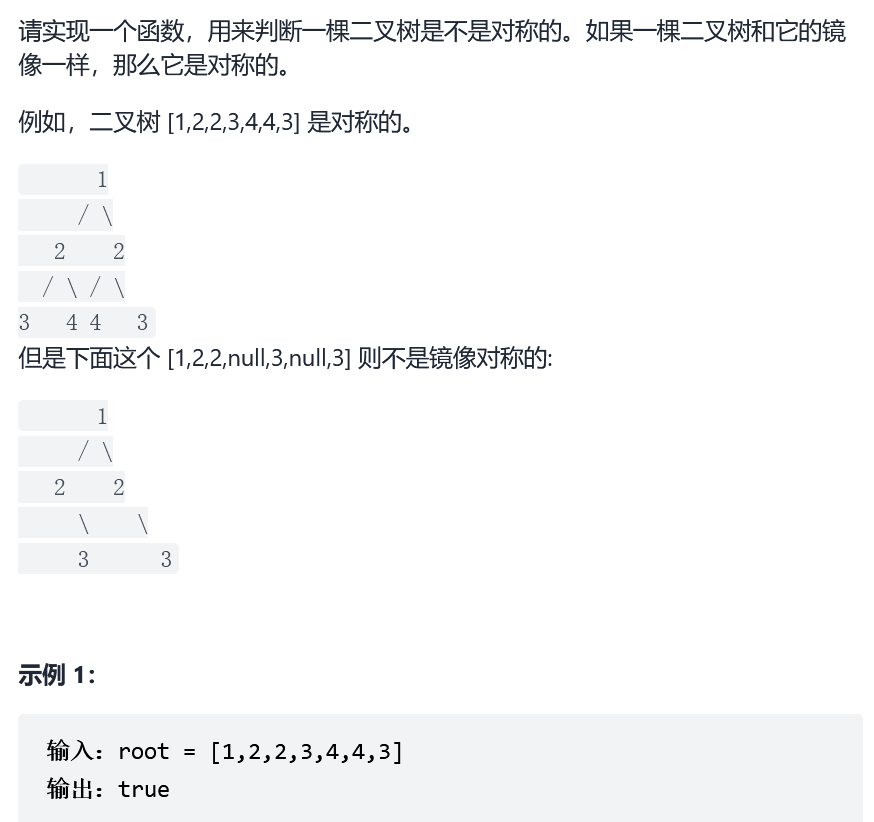
Idea: recursion is used to judge the left node L and right node R of the current node respectively. If it is a symmetric binary tree, there is L.val==R.val L.left.val==R.right.val L.right.val==R.left.val in the comparison function judge recursion
The termination conditions are:
- L R is null at the same time, that is, it crosses the leaf node at the same time, and returns true at this time
- L R does not cross the leaf node at the same time, and returns false
- They are not null, but the current values are different. false is returned
- If the recursion termination conditions of 1-3 are not met, the comparison will continue (A left comparison b right A right comparison B left)
Time complexity: O(n) n is the number of nodes. A pair of nodes can be judged at most n/2 times each time
Space complexity: O(n)
class Solution {
public boolean isSymmetric(TreeNode root) {
//If the tree is empty, return true directly
if(root==null)
return true;
return judge(root.left,root.right);
}
boolean judge(TreeNode leftTree,TreeNode rightTree)
{
//The left and right subtrees reach the leaf node at the same time, indicating symmetry
if(leftTree==null&&rightTree==null)
return true;
//The left and right subtrees do not reach the leaf node at the same time, indicating asymmetry
if(leftTree==null||rightTree==null)
return false;
//false is returned whenever the value of a node is different
if(leftTree.val!=rightTree.val)
return false;
//The current node is the same, but the left and right subtrees are not traversed. Continue to traverse
return judge(leftTree.left,rightTree.right) &&judge(leftTree.right,rightTree.left);
}
}
7. Sword finger Offer 12. Path in matrix
Sword finger Offer 12. Path in matrix

Idea: for deep search, there are m*n start positions. Pay attention to the termination conditions in the search function dfs. Note: a grid cannot be accessed multiple times in a search, so it needs to be set to '\ 0' to indicate that it has been accessed. After the search, return \ 0 to the original character (of course, you can also use another tag to access the array, but it will increase the space overhead)
Time complexity O(3) K ^K KMN): in the worst case, all schemes with a length of K string in the matrix need to be traversed, and the time complexity is O(3) K ^K K) ; there are Mn starting points in the matrix, and the time complexity is O(MN).
Number of schemes calculation: set the string length to K ,Each character in the search can be selected in four directions: up, down, left and right. The direction of turning back (the previous character) is discarded, leaving 333 choices. Therefore, the complexity of the number of schemes is O(3^K)
Space complexity O(K): the recursion depth during the search process does not exceed K, so the stack space accumulated by the system due to function calls occupies O(K) (because the stack space of the system call will be released after the function returns). In the worst case, K=MN, the recursion depth is Mn, and the system stack uses the additional space of O(MN)
class Solution {
public boolean exist(char[][] board, String word) {
int m=board.length;
int n=board[0].length;
int index=0;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
if(dfs(board,word,i,j,index))//m*n departure positions
return true;
}
return false;
}
public boolean dfs(char [][] board,String word,int i,int j,int index)
{
if(i<0||i>=board.length||j>=board[0].length||j<0||board[i][j]!=word.charAt(index))//Stop looking for conditions
return false;
if(index==word.length()-1)//Match successful
return true;
board[i][j]='\0';//Mark the (i,j) location as visited
boolean ans= dfs(board,word,i+1,j,index+1)||dfs(board,word,i,j+1,index+1)|| dfs(board,word,i-1,j,index+1)|| dfs(board,word,i,j-1,index+1);//Continue to search up, down, left and right. If one is true, don't write it separately, so it can't play the role of short circuit or
board[i][j]=word.charAt(index);//Restore tag
return ans;
}
}
8. Sword finger Offer 13. Motion range of robot

Idea: deep search is similar to the previous question, but there is a difference. There is only one starting point for this question. Since there is only one search and there is no need to visit again after visiting, there is no need to restore
class Solution {
int count=0;
public int movingCount(int m, int n, int k) {
//The tag array determines whether the (i,j) position has been accessed
boolean visited[][]=new boolean[m][n];
dfs(0,0,m,n,k,visited);//There is only one start position (0,0)
return count;
}
public void dfs(int i,int j,int m,int n,int k,boolean[][] visited)
{
if(i<0||i>=m||j<0||j>=n||visited[i][j]==true||calNum(i,j)>k)
return;//Termination conditions
count++;
visited[i][j]=true;//(i,j) location has been visited
dfs(i+1,j,m,n,k,visited);//Go down
dfs(i-1,j,m,n,k,visited);//Go up
dfs(i,j+1,m,n,k,visited);//turn right
dfs(i,j-1,m,n,k,visited);//Walk towards
//visited[i][j] there is no need to restore because there is only one search starting point
}
public int calNum(int i,int j)
{
//i. J is either 1 or 2 digits
int ans=i/10+i%10+j/10+j%10;//Calculate the sum of digits
return ans;
}
}
//O(mn)
//O(mn)
9. Sword finger Offer 34. Path with a certain value in binary tree
Sword finger Offer 34. A path with a certain value in a binary tree

Idea: depth first search is also a first order traversal for the tree. When traversing, judge whether the leaf node and whether the path sum is equal to the target
class Solution {
List<List<Integer>> ans=new ArrayList<>();
public List<List<Integer>> pathSum(TreeNode root, int target) {
List<Integer> list=new ArrayList<>();
dfs(root,target,list);
return ans;
}
public void dfs(TreeNode root,int target, List<Integer> list)
{
if(root==null)
return;
list.add(root.val); //Add current node
//Matches the node value and = target and is a leaf node
if(target==root.val&&root.left==null&&root.right==null)
{
ans.add(new ArrayList<>(list));//You must create a new with new
}
dfs(root.left,target-root.val,list);//Traverse left subtree
dfs(root.right,target-root.val,list);//Traversing right subtree
list.remove(list.size()-1);//The sum of the paths is not equal to target
//Path recovery: the newly added element needs to be deleted before backtracking
}
}
10. Sword finger Offer 36. Binary search tree and two-way linked list
Sword finger Offer 36. Binary search tree and bidirectional linked list
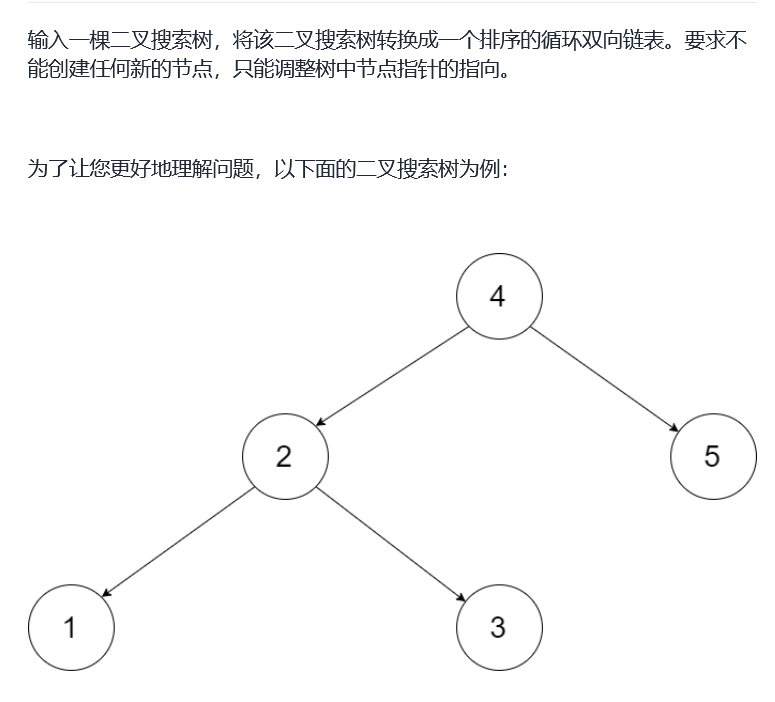
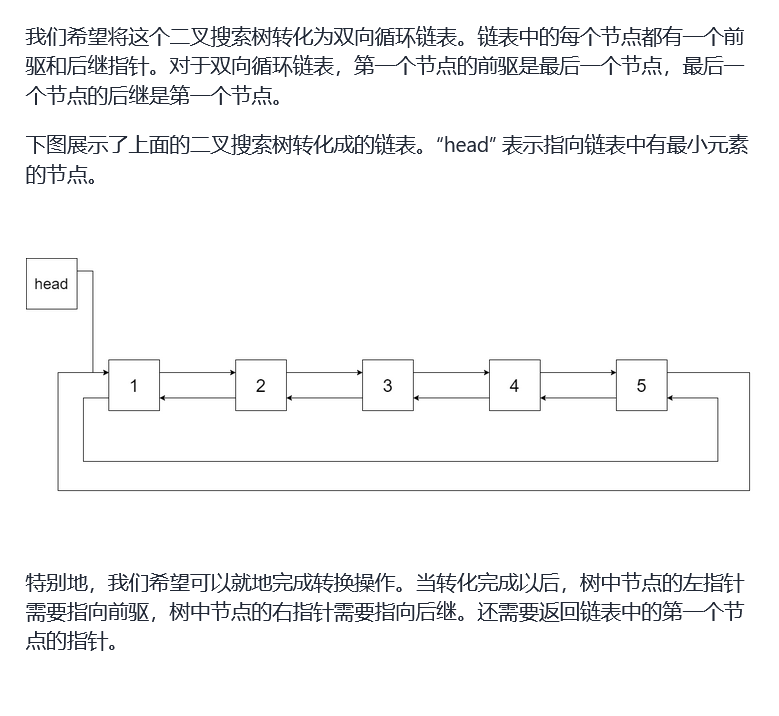
Idea:
- It requires ascending order and is a binary search tree, so it can be traversed in middle order
- When building the reference relationship between adjacent nodes, set the precursor node pre and the current node cur, not only pre.right = cur, but also cur.left = pre
- If the chain header node head and tail node tail are set, head.left = tail and tail.right = head should be constructed
class Solution {
Node head,pre;//The default value is null
public Node treeToDoublyList(Node root) {
if(root==null)//If the root is null, it will be returned directly. Otherwise, the head is null, and a null pointer exception will occur in head.left
return null;
dfs(root);
//The title requires that the head and tail are connected, and the head is finally pointing to the head, and the pre is pointing to the tail
head.left=pre;//The left pointer of head points to the pre tail node
pre.right=head;//The right pointer of pre points to the head node
return head;//Return header pointer
}
public void dfs(Node cur)
{
if(cur==null)
return;//Recursive end condition
dfs(cur.left);//Middle order traversal: left root right
if(pre==null)//If pre is empty, cur points to the first node
head=cur;//Therefore, the head points to the head node
else//Pre is not empty, indicating that cur points to a non head node and pre points to the previous node
pre.right=cur;//The right pointer of the previous node points to the current node
cur.left=pre;//The left pointer of the current node points to the previous node
pre=cur;//Save the current node for lower level recursive creation
dfs(cur.right);
}
}
//O (n) n is the number of nodes in the binary tree
//O(n)
11. Sword finger Offer 54. The k-th node of the binary search tree
Sword finger Offer 54. The k-th node of the binary search tree

Idea: because it is a binary search tree, the middle order traversal is in ascending order, and the last element is the largest. The title requires the k-largest, that is, the penultimate element after the middle order traversal. For convenience, you can get an inverse sequence of middle order traversal according to the traversal order of the right root and the left, which is the positive k-th element, and constantly make K -, K==0 indicates that the node with the largest K is found
class Solution {
int ans,k;//k should be set as a member variable
public int kthLargest(TreeNode root, int k) {
this.k=k;
inOrderReverse(root);
return ans;
}
public void inOrderReverse(TreeNode root)
{
if(root==null)
return;
//Medium order ascending order: left root right medium order reverse order: right root left
inOrderReverse(root.right);//Right root left
k--;//Count minus one
if(k==0)//Traverse to the k-th node, that is, the k-th node in reverse order
{
ans=root.val;
return;
}
inOrderReverse(root.left);
}
}
//O(n) in the worst case, the binary tree degenerates into a linked list with only right child nodes
//O(n)
12. Sword finger Offer 64. Find 1 + 2 +... + n
Sword finger Offer 64. Find 1 + 2 +... + n

Idea: use the short circuit of & & to realize the function of if judgment
class Solution {
int sum;
public int sumNums(int n) {
//x has no meaning, just to form a Boolean expression
//If n = 0, the following sumNums(n-1) will not go in, which is equivalent to an if judgment
boolean x=(n>0)&&(sumNums(n-1)>0);
sum+=n;
return sum;
}
}
//O(n)
//O(n)
13. Sword finger Offer 68 - I. nearest common ancestor of binary search tree
Sword finger Offer 68 - I. nearest common ancestor of binary search tree
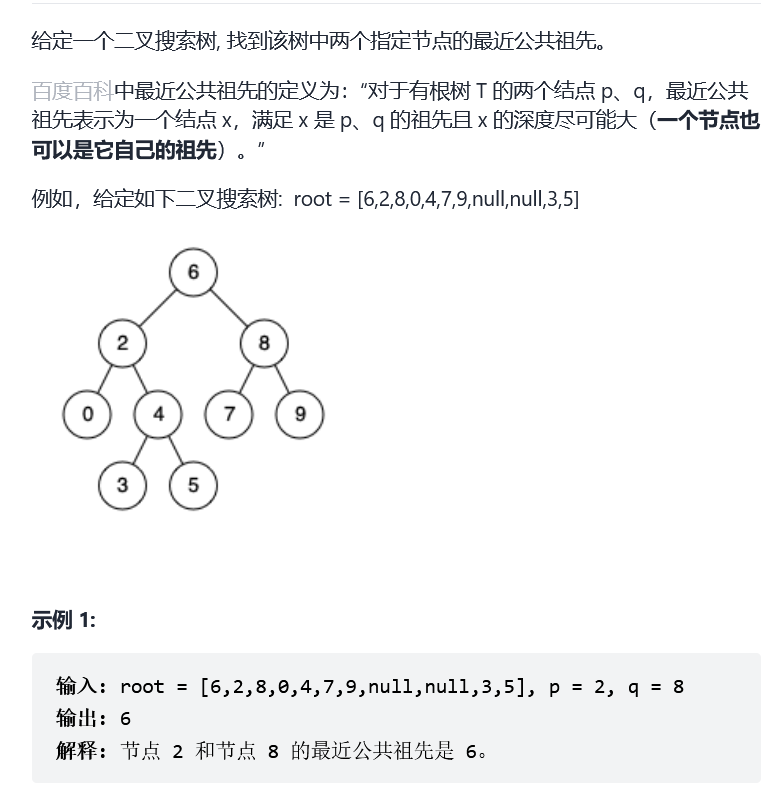
Idea: using the nature of binary search tree, the specific solution of left child node < root node < right child node can be iterative or recursive
//iteration
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
while(root!=null)
{
if(root.val>p.val&&root.val>q.val)//p q is located in the left subtree of the current root node
root=root.left;
else if(root.val<p.val&&root.val<q.val)//p q is located in the right subtree of the current root node
root=root.right;
else//The p q node is located in the left and right subtrees of the root node, indicating that root is the nearest public node
break;
}
}
}
//recursion
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root.val>p.val&&root.val>q.val)
return lowestCommonAncestor(root.left,p,q);
else if(root.val<p.val&&root.val<q.val)
return lowestCommonAncestor(root.right,p,q);
return root;
}
}
14. Sword finger Offer 68 - II. Nearest common ancestor of binary tree
Sword finger Offer 68 - II. Nearest common ancestor of binary tree

Idea: if root is the nearest common ancestor of P and Q nodes, it can only be one of the following three situations:
- p. Q is located in the left and right subtrees of root
- root=p,q is in the left or right subtree of root
- root=q,p is in the left or right subtree of root
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null)// If the tree is empty, null is returned directly
return null;
if(root==p||root==q)// If p and q are equal to root, their nearest common ancestor is root (a node can also be its own ancestor)
return root;
// Recursively traverse the left subtree. As long as p or q is found in the left subtree, whoever is found first will be returned
TreeNode left=lowestCommonAncestor(root.left,p,q);
// Recursively traverse the right subtree. As long as p or q is found in the right subtree, whoever is found first will be returned
TreeNode right=lowestCommonAncestor(root.right,p,q);
if(left==null&&right==null)
return null;
// If neither p nor q can be found in the left subtree, then both p and q must be in the right subtree. The closest common ancestor traversed in the right subtree is the nearest common ancestor (a node can also be its own ancestor)
if(left==null)
return right;
// If neither p nor q can be found in the right subtree, then both p and q must be in the left subtree. The first traversed in the left subtree is the nearest common ancestor (a node can also be its own ancestor)
if(right==null)//left!= null&&right!= Null indicates that root is the nearest public node
return left;
return root;
}
}
//O(n)
//O(n)
15. Sword finger Offer 37. Serialized binary tree
Sword finger Offer 37. Serialized binary tree
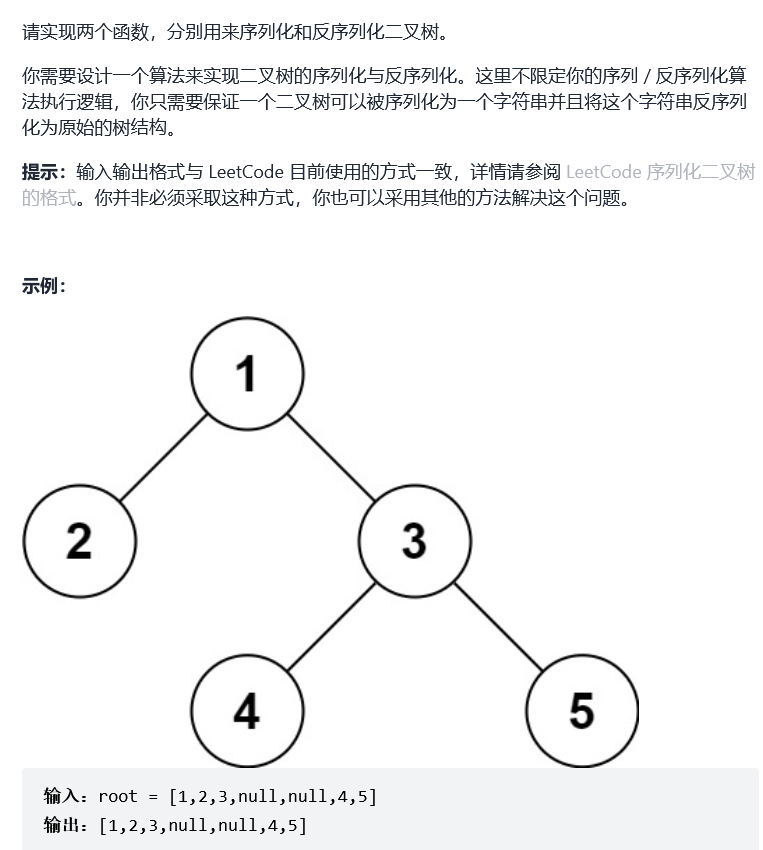
Idea: when using BFS or DFS, one thing to note is that you need to fill in the empty nodes of the binary tree to make the binary tree complete
DFS serialized sequence: 1,2, #, #, 3,4, #, #, 5, #, #, #,
BFS serialized sequence: 1,2,3, #, #, 4,5, #, #, #, #, #,
//DFS
public class Codec {
String SEP=",";//Separator representation
String NULL="#"; / / null pointer indicates
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
StringBuilder sb=new StringBuilder();
serialize(root,sb);
return sb.toString();
}
public void serialize(TreeNode root,StringBuilder sb)
{ if(root==null)
{
sb.append(NULL).append(SEP);
return;
}
//Preorder traversal
sb.append(root.val).append(SEP);
serialize(root.left,sb);
serialize(root.right,sb);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
String str[]=data.split(SEP);
LinkedList<String> nodes=new LinkedList<>();
for(String s:str)
{
nodes.addLast(s);
}
return deserialize(nodes);
}
public TreeNode deserialize(LinkedList<String> nodes)
{
String firstNode=nodes.removeFirst();//The first node of the preamble
if(firstNode.equals(NULL))//The element in the current nodes is null
return null;
TreeNode root=new TreeNode(Integer.parseInt(firstNode));
root.left=deserialize(nodes);
root.right=deserialize(nodes);
return root;
}
}
//O(n)
//O(n)
class Codec {
public:
char SEP=',';
string null_ptr="#";
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
string str;
serialize(root,str);
return str;
}
void serialize(TreeNode* root,string &str) {
if(root==NULL)
{
str+=(null_ptr+SEP);
return;
}
str+=to_string(root->val)+SEP;//In c + +, integers cannot be added directly to strings. First convert integers to strings
serialize(root->left,str);
serialize(root->right,str);
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
list<string> nodes;
string s;
for(int i=0;i<data.size();i++)
{
if(data[i]==SEP)
{
nodes.push_back(s);
s.clear();
}
else
{
s+=data[i];
}
}
return deserialize(nodes);
}
TreeNode* deserialize(list<string> &nodes)
{
string s=nodes.front();
nodes.pop_front();
if(s==null_ptr)
return NULL;//Null pointer in c + + is null, and null in Java
TreeNode *node=new TreeNode(stoi(s));//stoi is in the header file < CString >
node->left=deserialize(nodes);
node->right=deserialize(nodes);
return node;
}
};
//BFS
public class Codec {
String SEP=",";//Separator representation
String NULL="#";// Null pointer representation
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
if(root==null)
return "";
StringBuilder sb=new StringBuilder();
Queue<TreeNode> q=new LinkedList<>();
q.offer(root);
while(!q.isEmpty())
{
TreeNode node=q.poll();
if(node!=null)
{
sb.append(node.val).append(SEP);
q.offer(node.left);
q.offer(node.right);
}
else
sb.append(NULL).append(SEP);
}
// sb.deleteCharAt(sb.length());// Delete last comma
return sb.toString();
}
public TreeNode deserialize(String data)
{
if(data.equals(""))
return null;//Empty tree
//substring(1,data.length()-1) removes []
String val[]=data.split(SEP);
Queue<TreeNode> q=new LinkedList<>();
TreeNode root=new TreeNode(Integer.parseInt(val[0]));
q.offer(root);
int i=1;
while(!q.isEmpty())
{
TreeNode node=q.poll();
if(!val[i].equals(NULL))
{
node.left=new TreeNode(Integer.parseInt(val[i]));
q.offer(node.left);
}
i++;
if(!val[i].equals(NULL))
{
node.right=new TreeNode(Integer.parseInt(val[i]));
q.offer(node.right);
}
i++;
}
return root;
}
}
//O(n)
//O(n)
16. Sword finger Offer 38. Arrangement of strings
Sword finger Offer 38. Arrangement of strings
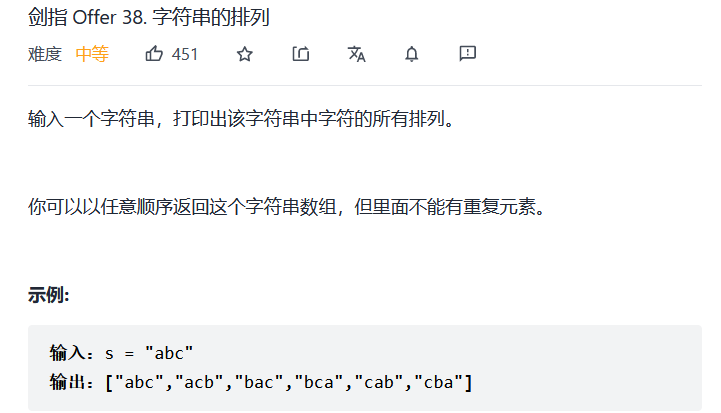
Idea: exchange, backtracking
class Solution {
ArrayList<String> lists=new ArrayList<>();
char c[];
public String[] permutation(String s) {
c=s.toCharArray();
backtrack(0);
return lists.toArray(new String[lists.size()]);
}
public void backtrack(int x)
{
if(x==c.length-1)
{
lists.add(String.valueOf(c));
return;
}
ArrayList<Character> list=new ArrayList<>();
for(int i=x;i<c.length;i++)
{
if(list.contains(c[i]))//Determine whether the element to be added is included
continue;
//If s="aab" we only need to fix the first a and skip the second a
list.add(c[i]);
swap(i,x);
backtrack(x+1);
swap(x,i);
}
}
//Switching to achieve full permutation
public void swap(int x,int i)
{
char tmp=c[i];
c[i]=c[x];
c[x]=tmp;
}
}
17. Sword finger Offer 55 - I. depth of binary tree
Sword finger Offer 55 - I. depth of binary tree
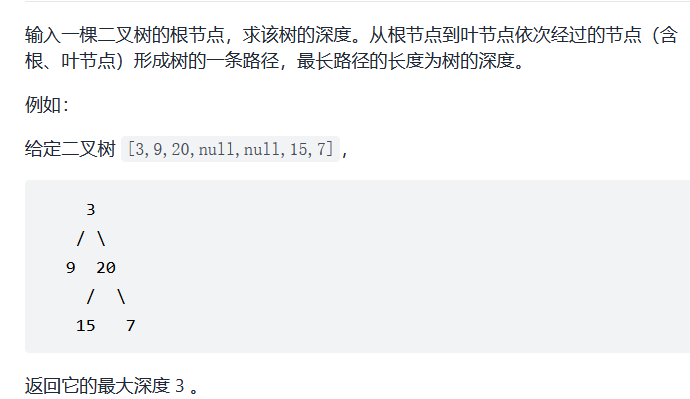
Idea 1: DFS
Time complexity: O(n)
Space complexity: O(n)
class Solution {
public int maxDepth(TreeNode root) {
if(root==null)
return 0;
return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
}
}
Idea 2: BFS
Time complexity: O(n)
Space complexity: O(n)
class Solution {
public int maxDepth(TreeNode root) {
if(root==null)
return 0;
int depth=0;
LinkedList<TreeNode> q=new LinkedList<>();
q.offer(root);
while(!q.isEmpty())
{
int sz=q.size();
for(int i=0;i<sz;i++)
{
TreeNode node=q.poll();
if(node.left!=null)
q.offer(node.left);
if(node.right!=null)
q.offer(node.right);
}
depth++;
}
return depth;
}
}
18. Sword finger Offer 55 - II. Balanced binary tree
Sword finger Offer 55 - II. Balanced binary tree
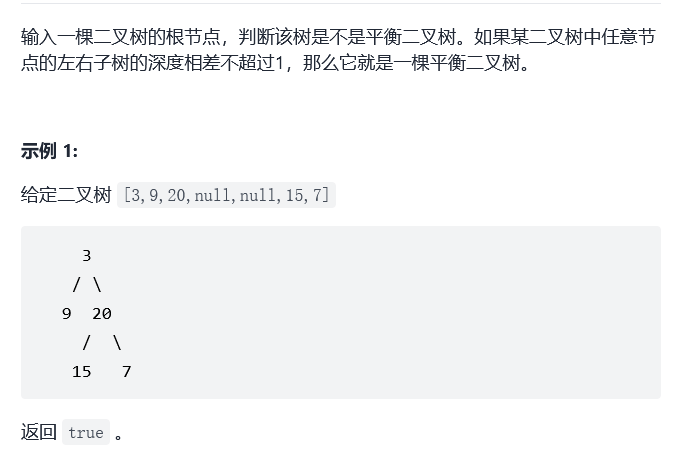
Idea: using the method of solving the maximum depth of binary tree in the previous problem, judge whether the maximum height difference between the left and right subtrees of each node is greater than 1
Time complexity: in the worst case, it is nlogn, and N is the number of nodes in the binary tree. For the full binary tree, the number of nodes in each layer is logn, and the time complexity of maxDepth operation in each layer is n
Spatial complexity: O(n) in the worst case, the binary tree degenerates into a linked list
class Solution {
public boolean isBalanced(TreeNode root) {
if(root==null)
return true;
if(Math.abs(maxDepth(root.left)-maxDepth(root.right))>1)
return false;
return isBalanced(root.left)&&isBalanced(root.right);
}
public int maxDepth(TreeNode root) {
if(root==null)
return 0;
return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
}
}