Time complexity and space complexity

Time complexity

Concept of time complexity

Definition of time complexity: in computer science, the time complexity of an algorithm is a function that quantitatively describes the running time of the algorithm. The time spent by an algorithm is directly proportional to the execution times of the statements in it. The execution times of the basic operations in the algorithm is the time complexity of the algorithm.

Asymptotic representation of large O

In fact, when we calculate the time complexity, we do not have to calculate the exact execution times, but only the approximate execution times
Asymptotic representation of large O.
Big O notation: a mathematical symbol used to describe the asymptotic behavior of a function.
Derivation of large O-order method:
1. Replace all addition constants in the run time with constant 1.
2. In the modified run times function, only the highest order term is retained.
3. If the highest order term exists and is not 1, the constant multiplied by this item is removed. The result is large O-order.

Examples

Constant order

  // O(1)
    private static void swap(Object[] arr, int i, int j){
        if(i < 0 || i >= arr.length)
            throw new IllegalArgumentException("i is out of bound.");
        if(j < 0 || j >= arr.length)
            throw new IllegalArgumentException("j is out of bound.");
        Object temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

Linear order

  // O(N)
    private static int sum(int n){
        if(n < 0)
            throw new IllegalArgumentException("n should be greater or equal to zero.");
        int ret = 0;
        for(int i = 0 ; i <= n ; i ++)
            ret += i;
        return ret;
    }

The code in the loop body of the above algorithm has been executed n times, so the time complexity is O(n).

Logarithmic order

  // O(logN)
    private static int binarySearch(Comparable[] arr, int n, int target){
        int l = 0, r = n-1;
        while( l <= r ){
            int mid = l + (r-l)/2;
            if(arr[mid].compareTo(target) == 0) return mid;
            if(arr[mid].compareTo(target) > 0) r = mid - 1;
            else l = mid + 1;
        }
        return -1;
    }

Square order

  // N ^ 2
    private static void selectionSort(Comparable[] arr, int n){
        for(int i = 0 ; i < n ; i ++){ // N
            int minIndex = i;
            for(int j = i + 1 ; j < n ; j ++) // N
                if(arr[j].compareTo(arr[minIndex]) < 0)
                    minIndex = j;

            swap(arr, i, minIndex);
        }
    }

Other complexity

In addition to constant order, linear order, square order and logarithmic order, there are the following time complexity:
When f(n)=nlogn, the time complexity is O(nlogn), which can be called nlogn order.
f(n)=n ³ The time complexity is O(n ³)， It can be called cubic order.
When f(n)=2 ⁿ, the time complexity is O(2 ⁿ), which can be called exponential order.
When f(n)=n!, the time complexity is O(n!), which can be called factorial order.
When f(n) = (√ n), the time complexity is O(√ n), which can be called square root order.

Complexity comparison

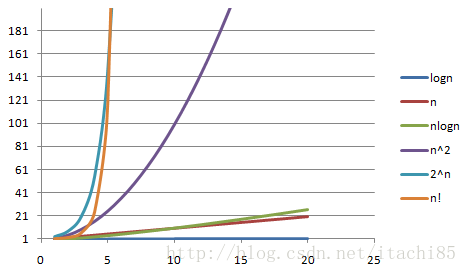
The x-axis represents the n value and the y-axis represents the T(n) value (time complexity). The T(n) value changes with the change of n value. It can be seen that the T(n) value of O(n!) and O(2 ⁿ) increases greatly with the increase of n value, while the T(n) value of O(logn), O(n) and O(nlogn) increases very little with the increase of n value.
The commonly used time complexity is in descending order according to the time spent:

O(1)<O(logn)<O(n)<O(nlogn)<O(n²)<O(n³)<O(2ⁿ)<O(n!)

Spatial complexity

Basic concepts

In short, space complexity is the amount of extra space opened up when the program runs

Space complexity is a measure of the amount of storage space temporarily occupied by an algorithm during operation. Space complexity is not how many bytes the program occupies, because it doesn't make much sense, so space complexity is the number of variables. Space complexity calculation rules are basically the same as practical complexity
Similarly, the large O asymptotic representation is used.

*Large O asymptotic representation

O(1)

// Calculate the spatial complexity of bubbleSort?
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
     boolean sorted = true;
     for (int i = 1; i < end; i++) {
         if (array[i - 1] > array[i]) {
             Swap(array, i - 1, i);
             sorted = false;
         }
     }
     if (sorted == true) {
         break;
     }
 }
}

O(N)

// How to calculate the spatial complexity of fibonacci?
int[] fibonacci(int n) {
long[] fibArray = new long[n + 1];
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; i++) {
  fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
 }
return fibArray; }