LCS problem is the problem of finding the longest common subsequence of two strings. The common solutions to this problem are ordinary recursive method and dynamic programming method.

• The general recursive method adopts the ideas of reducing and governing and dividing and governing. However, the algorithm has a large number of repeated calculations of subproblems, and its time complexity is exponential time complexity.
• DP method uses a two-dimensional array to record the results of each sub problem, so as to avoid repeated calculation of sub problems. It only needs to fill the array at one time according to a certain order, such as starting from bottom to top and starting from only one character. The last DP[m][n] is the result of the problem. At the same time, a solution result can be restored according to DP array. Its time complexity and space complexity are \ (\ Theta(mn) \).

Based on the observation of DP array, the author improves the dynamic programming method. A concrete example is given to explain how to improve the dynamic programming method.
The two strings are "EDUCATIONAL" and "advance" respectively. Find the longest common subsequence of the two strings, and its DP array is shown in the figure below:

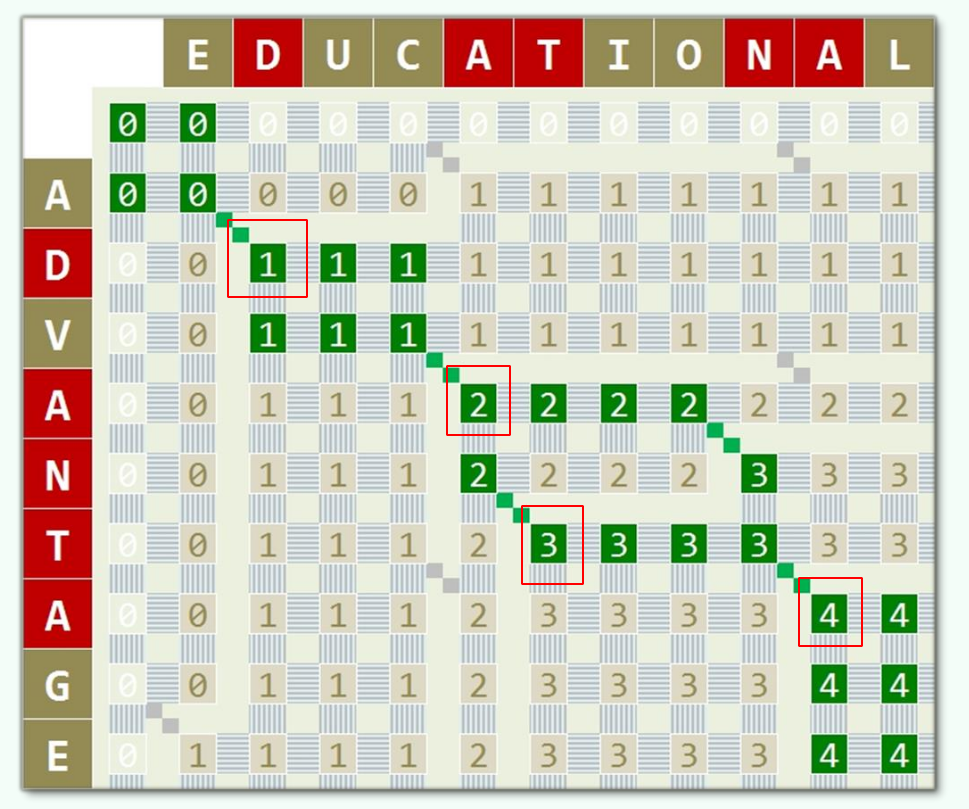
It can be observed that one solution of the longest common subsequence is DATA, which corresponds to the same letter. Take A as an example, it is the position of A in the first string and the second string and the smallest letter. The same is true for the remaining letters. Therefore, we can use this strategy to find the solution of an LSC, that is, to find the same characters in the two strings, Record the position of the character in the two strings. When the two positions and minimum, the character is the first character of the longest common subsequence. Record the coordinates of the character, represented by ir and jr. the second cycle starts from ir+1 and jr+1 to get the second character of the longest common subsequence, and so on.
In the process of writing the program, we need to consider the repeated letters. Here, a function is used to count the number of occurrences of the letter in the LSC solution and find the position of the letter in the two strings.
The condition for the end of the cycle is that the sum of the two coordinates has an initial value minpos. When the initial value of the minpos does not change, it means that no new letter satisfying the condition can be found, then the cycle ends. The time complexity is \ (\ O(mn*min(n,n)) \) and the space complexity is \ (\ O(1)). The procedure is as follows:

// LCS_DP_improve.cpp -- optimize the DP solution of LCs, make the space complexity constant, and get the composition of LCs at the same time
// Homework after class 3
// Space complexity O(1) time complexity O(mn*min(m,n))
#include <iostream>
#include <algorithm>
#include <string>
#include <cstring>
using std::string;

int timeschar(string s, char ch);               // Calculate the number of occurrences of ch in s
int searchpos(string s, char ch, int n);        // Calculate the position where the nth ch appears
int LCS_DP_improve(string A, string B, string & C);

int main()
{
    using namespace std;
    string str1 = "immaculate";
    string str2 = "computer";
    string str;
    int len = LCS_DP_improve(str1, str2, str);
    cout << str << endl;
    cout << "Length: " << len << endl;
    return 0;
}
int timeschar(string s, char ch)
{
    int len = s.size();
    int times = 0;
    for (int i = 0; i < len; i++)
        if (s[i] == ch)
            times++;
    return times;
}
int searchpos(string s, char ch, int n)
{
    int len = s.size();
    int timesch = 0;
    for (int i = 0; i < len; i++)
        if (s[i] == ch)
        {
            timesch++;
            if (timesch == n)
                return i;
        }
    return -1;          // Not found, this problem does not exist
}
int LCS_DP_improve(string A, string B, string & C)
{
    int lenA = A.size();
    int lenB = B.size();
    int minlen = lenA > lenB ? lenB : lenA; // Calculate the minimum length of A and B
    int ir = -1;     // Where do you like to start every time
    int jr = -1;     // Same as ir
    string tempA;    // Record the location of each search
    for (int k = 0; k < minlen; k++)
    {
        int minpos = lenA + lenB;         // Record the coordinates of the smallest x and y when they are equal, and the initial value is the maximum value
        char ch;    //Record the letters found
        for (int i = ir + 1; i < lenA; i++)
            for (int j = jr + 1; j < lenB; j++)
                if(A[i] == B[j])
                {
                    if (minpos > i + j)
                    {
                        minpos = i + j;
                        ch = A[i];
                    }
                }
        if (minpos == lenA + lenB)      // Conditions for terminating the cycle
            break;
        C.push_back(ch);
        int timech = timeschar(C, ch);
        ir = searchpos(A, ch, timech);
        jr = minpos - ir;
    }
    return C.size();
}