mathematical knowledge

1. Whether a combined number is odd: when C(n,k) is odd, n & K = = K.

2. Rational modulus: Rational number modulo fractional modulo Fermat small theorem

Other games

1.Teacher Zhang and CAI waiwu's game

• Given a and B (a > b), what number can be obtained by a + b or a - B transformation? In fact, we can get a + x, x takes GCD (GCD (a, a - b), GCD (B, a - b)).

2.B. T-primes

• This question is really new. Let's find an integer with three factors. First, let's analyze the number A. since there is only one factor that is not 1 or a, the square of this factor must be equal to a, otherwise there can't be only one factor. Suppose a has a factor B (1 < B < a), then it must exist (1 < C < a), so that b * c = a. Therefore, only when b = c will there be a factor that is not equal to 1 or a.
• Therefore, we can make an angstrom sieve first, but this problem only asks whether it is a prime number, so we only construct is_prime is the array.

3.Problem E: Expired License

• There are two holes in this problem:
• 0.00007 * 100000 is represented by floating-point number, which is 6.99999999999991118... So it needs to be rounded.
• Note that when the input number a = b, it will be reduced to the form of 1 and 1, but in fact, 2 and 2 meet the requirements. Just such a special case.

4.B Basic Gcd Problem

• The problem is to find the number of prime factors. But you can't use the previous method of finding the prime factor, which is O ( n 3 2 ) O(n^{\frac{3}{2}}) O(n23), but the teammates came up with about O ( n ) O(n) Processing speed of O(n).
• The second step is very simple. It's just calculation c k c^k ck, k is the number of prime factors contained in n.
• The board still needs to be learned.

#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn = 1000010;
const ll mod = 1000000007;
int f[maxn];
void pre(int N) {
	for (int i = 2; i <= N; i++) f[i] = 1;
	for (int i = 2; i <= N; i++) {
		for (int j = 2; j <= i && j * i <= N; j++) f[i * j] = f[i] + f[j];
	}
}
ll mod_pow(ll x, ll n) {
	ll res = 1;
	while (n) {
		if (n & 1) res = res * x % mod;
		x = x * x % mod;
		n >>= 1;
	}
	return res;
}
int main() {
	pre(1000000);
	int T;
	scanf("%d", &T);
	while (T--) {
		ll c, n;
		scanf("%lld%lld", &n, &c);
		printf("%lld\n", mod_pow(c, (ll)f[n]));
	}
	return 0;
}

cf

1.C. Celex Update

• This question is really interesting. I first found that from (1,1) to (3,3), I found that the values of two roads are the same. Then I found that the first road was one grid earlier than the second road, and then one grid later than the second road. Then I guess the two roads are the same because of this. Then it is observed that the coordinates of X corresponding to the first path moving downward are (1,3) and the second path is (2,2). Then it is felt that as long as the sum of the corresponding x coordinates is equal, it is the same. Well, it depends on how many of these one-dimensional vectors are different from each other. The minimum is (x1, x1,... X1), and x1 * dy, the maximum is (x2, x2,... x2), and X2 * Dy, and then the answer is x2 * dy - x2 * dy + 1 = dx * dy + 1. It's a test of thinking.

2.C. Mixing Water

• I want to add an error code to remind myself that int will explode in such a place. Sometimes this priority is hard to say, so it's better to bypass it as much as possible.
• (double)(x + 1) * h, this step will explode int.

#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
int main() {
	int T;
	scanf("%d", &T);
	while (T--) {
		int h, c, t;
		scanf("%d%d%d", &h, &c, &t);
		if (h + c >= 2 * t) {
			printf("2\n");
		}
		else {
			int x = (t - h) / (h + c - 2 * t);
			double tmp1 = ((double)(x + 1) * h + x * c) / (double)(2 * x + 1);
			double tmp2 = ((double)(x + 2) * h + (x + 1) * c) / (double)(2 * x + 3);
			if (fabs(tmp1 - t) > fabs(tmp2 - t)) {
				x++;
			}
			printf("%d\n", x * 2 + 1);
		}
	}
	return 0;
}

3.J Easy Integration

Formula derivation:

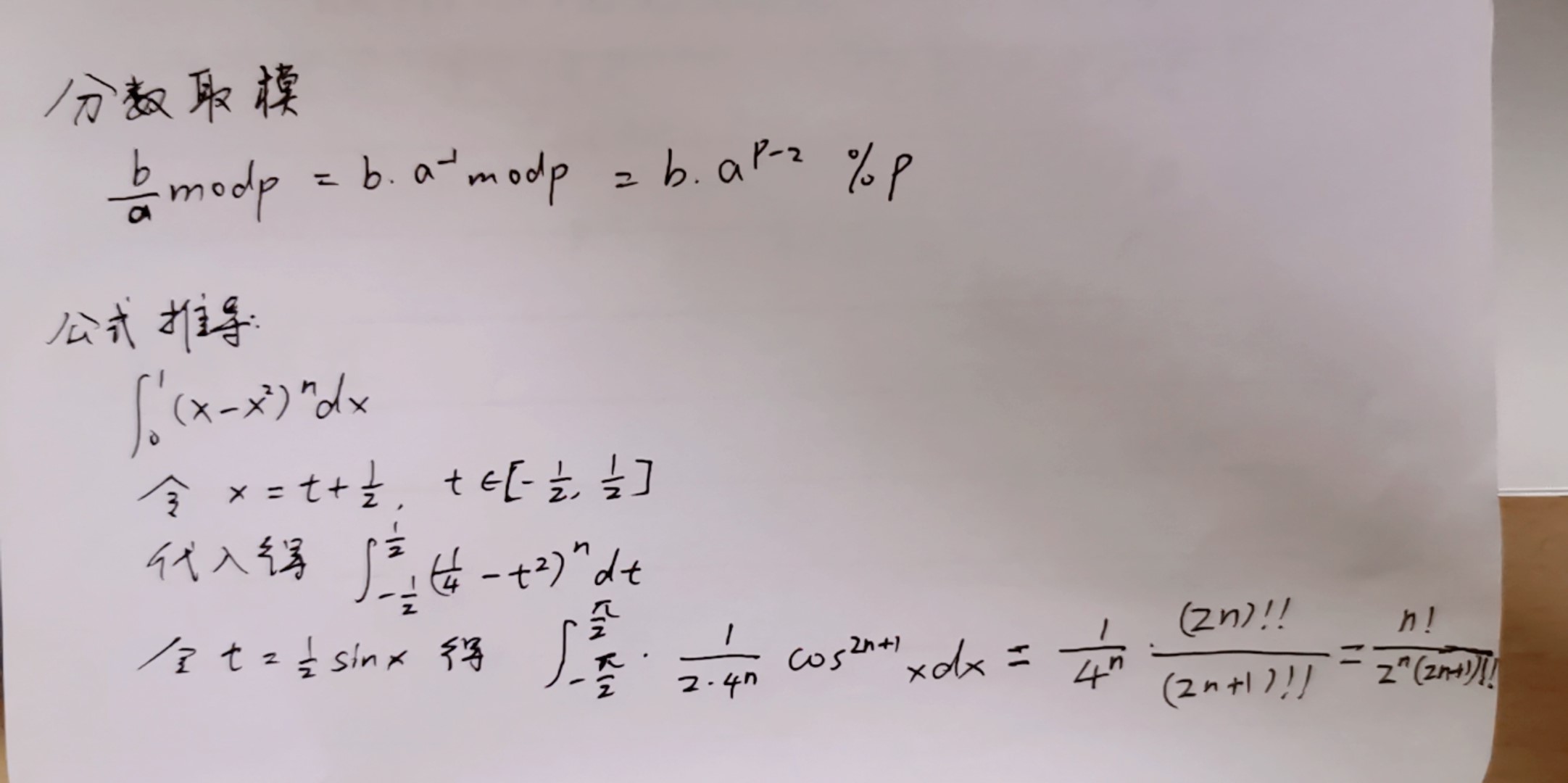
​​​​​#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const ll mod = 998244353;
const ll mod_2 = mod - 2;
ll a[1000010] = { 1LL }, b[1000010] = { 1LL }, c[1000010] = { 1LL };
void pre() {
	int N = 1000000;
	for (int i = 1; i <= N; i++) {
		a[i] = (a[i - 1] << 1LL) % mod;
		b[i] = b[i - 1] * (2LL * i % mod + 1) % mod;
		c[i] = c[i - 1] * i % mod;
	}
}
ll mod_pow(ll x) {
	ll res = 1;
	ll n = mod_2;
	while (n > 0) {
		if (n & 1) res = res * x % mod;
		x = x * x % mod;
		n >>= 1;
	}
	return res;
}
int main() {
	pre();
	ll N;
	while (scanf("%lld", &N) == 1) {
		ll ans = mod_pow(a[N] * b[N] % mod) * c[N] % mod;
		printf("%lld\n", ans);
	}
	return 0;
}