0x01. Related concepts

1. AOV network: in a directed graph that represents engineering, activity is represented by vertex, and priority relationship between activities is represented by arc. Such a directed graph is a network that represents activity by vertex, which we call AOV network.
2. Topology sequence: setting 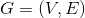Is a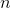 Directed graph of vertices, 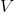Vertex sequence in 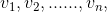Satisfied if from vertex 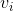To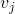 If there is a path, the vertices in the vertex sequence 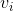Must be at vertex 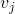Before. We call such a sequence of vertices a topological sequence.
3. Topological sorting: the process of constructing topological sequences for a directed graph.
4. AOE network: in a directed graph representing a living project, the vertex is used to represent the event, the directed edge is used to represent the activity, and the weight on the edge is used to represent the duration of the activity. The edge of this directed graph represents the active network, which we call the AOE network.
5. Critical path: we call the sum of the duration of each activity on the path as the path length, and the path with the maximum length from the source point to the sink point as the critical path.
6. Key activities: activities on the critical path are called key activities.

0x02. Understand AOV network and AOE network

AOV network and AOE network are directed graphs of engineering. AOV network weight represents yo priority relationship and AOE network weight represents duration.

AOV net:

AOE net:

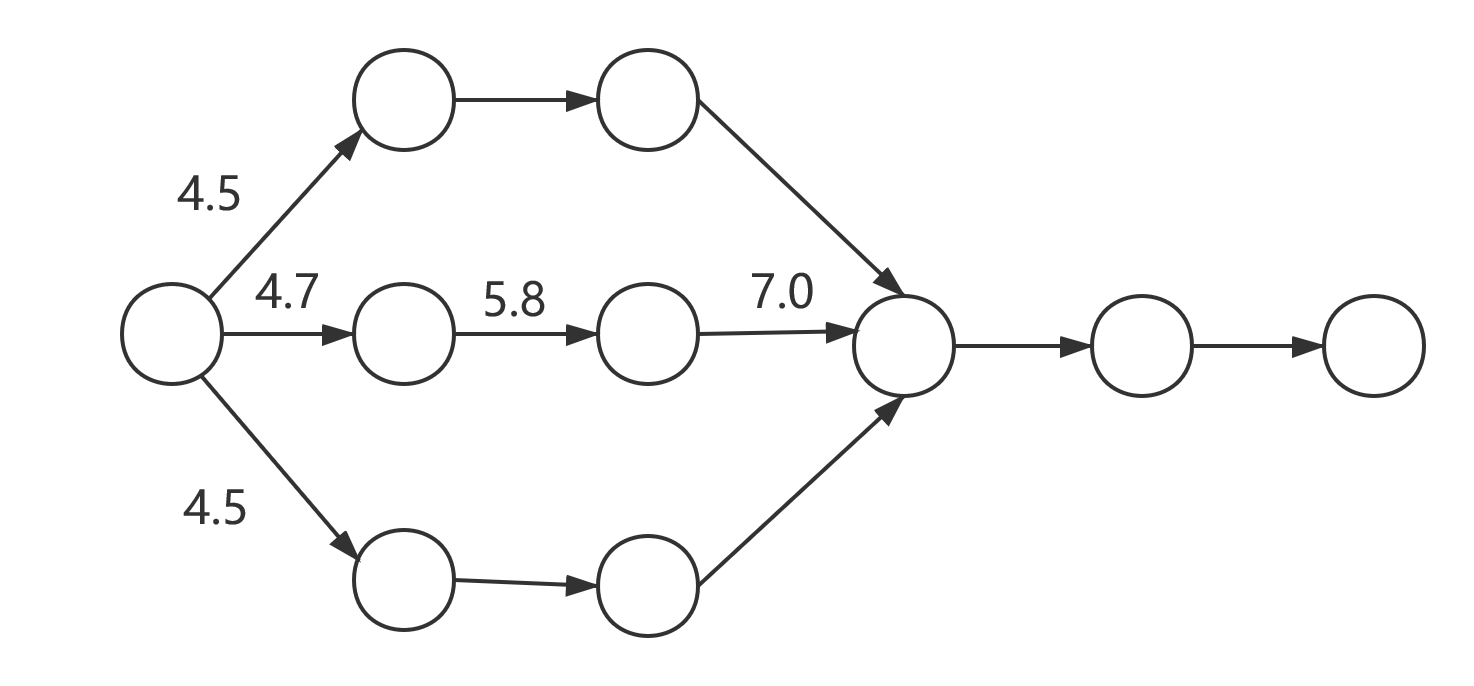
0x03. Topological sorting algorithm

Basic principle:

Select a vertex with an entry of 0 to output from the AOV network, delete the vertex, delete the arc with the vertex as the tail, and continue to repeat this step until all the vertices are output or there is no vertex with an entry of 0 in the AOV network. If there is still a ring, it cannot form a topological sequence.

Because of the need for in degree information and delete operation, the adjacency table structure is needed, but the in degree information is also needed. The cross linked list is too cumbersome. The best way is to manually input the in degree of a vertex, so the vertex structure is composed of in, data, firstedge. You need to use the stack to store the vertices with a degree of 0.

Code:

int TopologicalAort(GraphAdjList GL)
{
	EdgeNode* e;
	int i, k, gettop;
	int top = -1;//Stack pointer
	int count = 0;//Count the number of output vertices
	int* stack;//This stack is stored in the vertex of degree 0
	stack = (int*)malloc(GL.numv*sizeof(int));
	for (i = 0;i < GL.numv; i++)
	{
		if (GL.adjList[i].in == 0)
		{
			stack[++top] = i;
		}
	}
	while (top != -1)
	{
		gettop=stack[top--];//Stack out
		printf("%c->", GL.adjList[gettop].data);//Output node
		count++;
		for (e = GL.adjList[i].firstedge; e; e = e->next)//Access adjacent edge
		{
			k = e->adjvex;
			if (!(--GL.adjList[k].in))
			{
				stack[++top] = k;
			}
		}
	}
	if (count < GL.numv)
	{
		return false;
	}
	else
	{
		return true;
	}
}

0x04. Critical path

Because AOE network involves the relationship of time, we need to understand several concepts first.

• earliest time of vertex: vertex 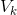The earliest occurrence time of.
• ltv (last time of vertex): vertex 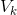The latest occurrence time of.
• earliest time of edge: Arc 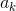The earliest occurrence time of.
• lte (last time of edge): Arc 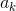The latest occurrence time of.

First of all, we need to find the earliest event etv. In this step, we can find it at the same time of topological sorting.

An improved topological sorting algorithm for finding critical paths:

//First, you need to define several variables
int* etv, * ltv;//Find the earliest and latest occurrence time of each vertex
int* stack2;//Storage topology sequence
int top2;
int TopologicalAort1(GraphAdjList GL)
{
	EdgeNode* e;
	int i, k, gettop;
	int top = -1;
	int count = 0;
	int* stack;
	stack = (int*)malloc(GL.numv * sizeof(int));
	for (i = 0; i < GL.numv; i++)
	{
		if (GL.adjList[i].in == 0)
		{
			stack[++top] = i;
		}
	}
	top2 = -1;
	etv = (int*)malloc(GL.numv * sizeof(int));
	for (i = 0; i < GL.numv; i++)//The earliest time the initialization event occurred
	{
		etv[i] = 0;
	}
	stack2= (int*)malloc(GL.numv * sizeof(int));
	while (top != -1)
	{
		gettop = stack[top--];
		count++;
		stack[++top2] = gettop;//Save topology sequence
		for (e = GL.adjList[gettop].firstedge; e; e = e->next)
		{
			k = e->adjvex;
			if (!(--GL.adjList[k].in))
			{
				stack[++top] = k;
			}
			if ((etv[gettop] + e->weight) > etv[k])//Find etv array
			{
				etv[k] = etv[gettop] + e->weight;
			}
		}
	}
	if (count < GL.numv)
	{
		return false;
	}
	else
	{
		return true;
	}
}

The purpose of this improvement is to find the etv array. The way to find the etv array is to find the starting point of this vertex, and then find the longest path from the starting point to this vertex.

When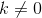 At that time, 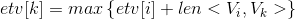. For example, if vertex V3 has < V1, V3 >, < V2, V3 >, two arcs, ETV [3] = max {ETV [2] + len < V2, V3 >, ETV [1] + len < V1, V3 >}.

Critical path algorithm:

void CrticalPath(GraphAdjList GL)
{
	EdgeNode* e;
	int i, gettop, k, j;
	TopologicalAort1(GL);
	int ete, lte;//The earliest and latest occurrence time of the activity
	ltv= (int*)malloc(GL.numv * sizeof(int));
	for (i = 0; i < GL.numv; i++)//Initialize ltv array
	{
		ltv[i] = etv[GL.numv-1];//Set all to the maximum value in etv
	}
	while (top2 != -1)
	{
		gettop = stack2[top2--];
		for (e = GL.adjList[gettop].firstedge; e; e = e->next)
		{
			k = e->adjvex;
			if (ltv[k] - e->weight < ltv[gettop])//Find the ltv array
			{
				ltv[gettop] = ltv[k] - e->weight;
			}
		}
	}
	for (j = 0; j < GL.numv; j++)//Traverse the arc table of each vertex
	{
		for (e = GL.adjList[j].firstedge; e; e = e->next)
		{
			k = e->adjvex;
			ete = etv[j];
			lte = ltv[k] - e->weight;
			if (ete == lte)//The earliest start time of the activity is equal to the latest start time, which is the key path
			{
				printf("(%c->%c),weight=%d", GL.adjList[j].data, GL.adjList[k].data, e->weight);
			}
		}
	}
}

Algorithm principle analysis:

In the first half of the algorithm, the ltv array is calculated by using the stack of the generated topological sequence. The latest start time should be deduced from the back to the front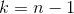 At that time,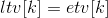Because the last activity to be completed must be the last activity, and there is no other choice. If it is not the last activity, then[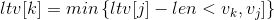For example, if a vertex V7 has < V7, V8 >, < V7, V9 > two arcs, then ltv[7] should be equal to min {LTV [8] - len < V7, V8 > (the length of this arc), LTV [9] - len < V7, V9 >.

When determining the shortest path, ete and lte appear. These two concepts are all for the arc. Ete, the earliest start time of the arc, should be equal to the earliest start time of the arc tail, lte, the latest start time of the arc, should be equal to the latest start time of the arc head - the weight of the arc.

If ete is equal to lte, it means that this arc is the arc on the critical path. Because if the earliest start time and the latest start time of an arc are not equal, it means that there is free in the middle and other activities can be completed. Then this is not the critical path. The critical path is the longest path in the whole network, and there is no free from the beginning to the end.

 

 

 

The end of this chapter.