Topology sorting topoport
Topological sorting of a directed acyclic graph G is to arrange all vertices in G into a linear sequence so that any pair of vertices in the graph u u u and v v v. Ruo Bian < u , v > ∈ E ( G ) <u,v>∈E(G) < u, V > ∈ E(G), then u appears in the linear sequence v v v before. Generally, such a linear sequence is called a sequence satisfying topological order, which is called topological sequence for short. In short, a partial order on a set is used to obtain a total order on the set. This operation is called topological sorting.
Topological sorting and edge deletion steps
- Count the penetration of all points
- Delete the edge connected to the point output with a penetration of 0
- Repeat until all points are deleted
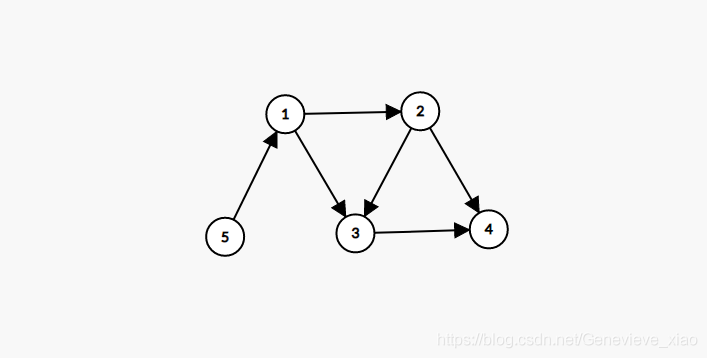
Output 5
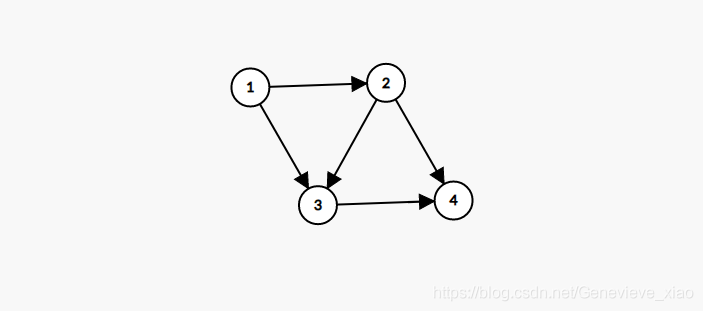
Output 5 1
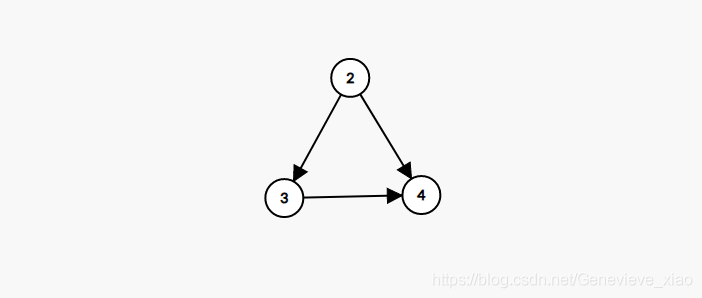
Output 5 1 2
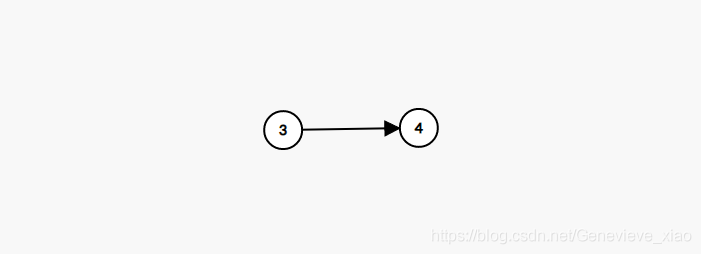
Output 5 1 2 3

Output 5 1 2 3 4
sort
P1347 [topological sorting template] Luogu portal
Title Description
An ascending sequence of different values refers to a sequence in which the elements increase from left to right, for example, an ordered sequence
A
,
B
,
C
,
D
A,B,C,D
A. B, C, d represent
A
<
B
,
B
<
C
,
C
<
D
A<B,B<C,C<D
A<B,B<C,C<D. In this problem, we will give you a series of forms such as
A
<
B
A<B
A < B, and ask you to judge whether you can determine the order of this sequence according to these relationships.
Input format
The first line has two positive integers
n
,
m
n,m
n,m,
n
n
n indicates the number of elements to be sorted,
2
≤
n
≤
26
2≤n≤26
2 ≤ n ≤ 26, th
1
1
1 to
n
n
n elements will be capitalized
A
,
B
,
C
,
D
A,B,C,D
A. B, C, D.
m
m
m represents the shape to be given, such as
A
<
B
A<B
The number of relationships with a < B.
Next there are m m m rows, each row has 3 3 Three characters, one capital letter, one < symbol and one capital letter respectively, represent the relationship between the two elements.
Output format
If according to the previous x x This can be determined by x relationships n n Order of n elements YYY Y (if any) A B C ABC ABC), output
Sorted sequence determined after xxx relations: yyy...y.
If according to the previous x x x relationships are found to be contradictory (e.g A < B , B < C , C < A A<B,B<C,C<A A < B, B < C, C < a), output
Inconsistency found after x relations.
If according to this m m m relationships cannot be determined n n Order of n elements, output
Sorted sequence cannot be determined.
(prompt: OK) n n The program can be ended after the sequence of n elements, without considering the contradiction after determining the sequence)
Input sample 1
4 6 A<B A<C B<C C<D B<D A<B
Output sample 1
Sorted sequence determined after 4 relations: ABCD.
Input sample 1
3 2 A<B B<A
Output sample 1
Inconsistency found after 2 relations.
Input sample 1
26 1 A<Z
Output sample 1
Sorted sequence cannot be determined.
//P1347 sorting topology sorting solution
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#define maxn 30
#define maxm 700
using namespace std;
int n,m,len,cnt,c;
int head[maxn],vis[maxn],dis[maxn];
//Chained forward star head[] vis [] marker dis [] topological chain length
int f[maxn],in[maxn],qq[maxn];
//f in temporary qq record queue
struct node{
int to,next;
}e[maxm];
//Linked list
void add(int u,int v){
cnt++;
e[cnt].to=v;
e[cnt].next=head[u];
head[u]=cnt;
}//Edging
queue<int>q;//queue
//Topological sorting
void topo(){
//initialization
memset(dis,0,sizeof dis);
memset(vis,0,sizeof vis);
memset(qq,0,sizeof qq);
len=c=0;
for(int i=1;i<=n;i++){
in[i]=f[i]; //Temporary storage initialization
if(in[i]==0){ //Initial penetration = = 0 indicates that it is the root node
q.push(i); //Join the team
vis[i]=1; //Queue mark
dis[i]=1; //Length 1
}
}
while(!q.empty() ){
int t=q.front() ; q.pop() ; qq[++c]=t; //Take the lead
//Chained forward star traversal
for(int i=head[t];i;i=e[i].next ){
int v=e[i].to ; //Make a brief note
if(vis[v]!=0) continue; //Skip after marking
//Take the longest chain length
dis[v]=max(dis[v],dis[t]+1);
len=max(len,dis[v]);
in[v]--;//Penetration--
if(in[v]==0){ //Join = = 0 join the team
q.push(v);
vis[v]=1;
}
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
char ch,u,v;
cin>>u>>ch>>v;
//Special judgment 1: a < a contradiction
if(u==v){
printf("Inconsistency found after %d relations.",i);
return 0;
}
add(u-64,v-64); //The edge is added from the small point to the large point to ensure ascending output
f[v-64]++; //Penetration++
topo();
//Special judgment 2: longest chain length = = n qualified output
if(len==n){
printf("Sorted sequence determined after %d relations: ",i);
for(int j=1;j<=n;j++){
printf("%c",qq[j]+64);
}
printf(".\n");
return 0;
}
//Special judgment 3: there is a ring contradiction
for(int j=1;j<=n;j++){
if(in[j]){ //Penetration= 0
printf("Inconsistency found after %d relations.",i);
return 0;
}
}
}
//Special judgment 4: the chain with length n cannot be formed
printf("Sorted sequence cannot be determined.");
return 0;
}
It can also be solved by Floyd
//P1347 sorting floyd method
#include<iostream>
#include<cstdio>
#define inf 0x3f3f3f3f
#define maxn 30
using namespace std;
int n,m,dis[maxn][maxn],q[maxn];
//initialization
void stat(){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i!=j) dis[i][j]=inf;
}
}
}
//Bare floyd shortest
void floyd(){
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
}
int main(){
scanf("%d%d",&n,&m);
stat();
for(int k=1;k<=m;k++){
char ch,u,v;
cin>>u>>ch>>v;
dis[u-64][v-64]=1;
//Special judgment 1: a < a contradiction
if(u==v) {
printf("Inconsistency found after %d relations.",k);
return 0;
}
floyd();
int anscnt=0;
for(int i=1;i<=n;i++){
int cnt1=0,cnt2=0;
for(int j=1;j<=n;j++){
if(i==j) continue;
//Special judgment 2: there is a ring contradiction
if(dis[i][j]!=inf && dis[j][i]!=inf ){
printf("Inconsistency found after %d relations.",k);
return 0;
}
if(dis[i][j]!=inf) cnt1++; //Number of points that can be reached
if(dis[j][i]!=inf) cnt2++; //Number of points that can be reached
}
if(cnt1+cnt2==n-1) q[cnt2+1]=i, anscnt++; //This point can be determined
}
if(anscnt==n){ //All points can be determined. Special judgment 3: compliance output
printf("Sorted sequence determined after %d relations: ",k);
for(int j=1;j<=n;j++){
printf("%c",q[j]+64);
}
printf(".\n");
return 0;
}
}
//Special judgment 4: the chain with length n cannot be formed
printf("Sorted sequence cannot be determined.");
return 0;
}
information transfer
P2661 information transmission Luogu portal
Title Description
have
n
n
n students (No
1
1
1 to
n
n
n) Playing a game of information transmission. In the game, everyone has a fixed information transmission object, in which the number is
i
i
The information transmission object of i's students is No
T
i
T_i
Ti's classmate.
At the beginning of the game, everyone only knows his birthday. In each subsequent round, Everyone will tell their current birthday information to their information transmission object at the same time (Note: someone may get information from several people, but each person will only tell the information to one person, that is, their own information transmission object). When someone knows their birthday from others, the game ends. How many rounds of the game can be played?
Input format
2 lines in total.
Line 1 contains
1
1
1 positive integer
n
n
n. Show
n
n
n people.
Line 2 contains
n
n
n positive integers separated by spaces
T
1
,
T
2
.
.
.
,
T
n
T_1,T_2...,T_n
T1,T2..., Tn, where No
i
i
i integers
T
i
T_i
Ti , indicates No
i
i
The information transmission object of i's students is No
T
i
T_i
Ti's classmates,
T
i
≤
n
T_i ≤n
Ti ≤ n and
T
i
≠
i
T_i ≠ i
Ti=i.
Output format
1
1
An integer indicating the total number of rounds of the game.
sample input
5 2 4 2 3 1
sample output
3
Data range
about
30
30%
30,
n
≤
200
n ≤ 200
n≤200;
about
60
60%
60 data,
n
≤
2500
n ≤ 2500
n≤2500;
about
100
100%
100 data,
n
≤
200000
n ≤ 200000
n≤200000.
#include<iostream>
#include<cstdio>
#include<queue>
#define maxn 200005
using namespace std;
int n,head[maxn],in[maxn],vis[maxn],cnt;
//Chain head [] penetration in [] mark vis []
int ans=1e9,dep;
//ans minimum ring dep is the size of the dfs ring for each pass
struct node{
int to,next;
}e[maxn];
//Edging
void add(int u,int v){
cnt++;
e[cnt].to =v;
e[cnt].next =head[u];
head[u]=cnt;
}
//Search the smallest ring after deleting the edge
void dfs(int k,int f){ //Current point k end point f
dep++; //Ring size++
for(int i=head[k];i;i=e[i].next ){
int v=e[i].to;
if(v!=f) dfs(v,f), vis[v]=1;
//Judge whether the point is the end point, otherwise continue dfs and mark
}
}
//Topological sorting and edge deletion
void topo(){
queue<int>q;
for(int i=1;i<=n;i++){
if(in[i]==0){ //The initial entry level is 0, and the entry mark is 0
q.push(i);
vis[i]=1;
}
}
while(!q.empty()){
int t=q.front() ; q.pop() ;//Take the lead
for(int i=head[t];i;i=e[i].next ){ //Chained forward star traversal
int v=e[i].to; //Mark points
in[v]--; //Penetration of exit point--
if(in[v]==0){ //If the entry degree is 0, the team is marked
q.push(v); vis[v]=1;
}
}
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
int x;
scanf("%d",&x);
add(i,x); //Edging
in[x]++; //Penetration++
}
topo();
//After deleting the edge, the vis of the point on the ring is still 0
for(int i=1;i<=n;i++){
if(!vis[i]){ //The points on the ring are dfs
dep=0;
dfs(i,i); //Start i end i
ans=min(dep,ans); //Take the smallest ring
}
}
printf("%d",ans);
}