Algorithmic thought
Definition of bipartite graph: if all vertices of a graph can be divided into X X X and Y Y Y two sets, and for all edges, the two points of the edge do not belong to the same set, then this graph is a bipartite graph
A more accurate definition is as follows:
G
=
(
V
,
E
)
G=(V,E)
G=(V,E) is an undirected graph,
V
V
V is the point set,
E
E
E is the edge set, if
V
V
V can be divided into two disjoint subsets
(
V
1
,
V
2
)
(V_1,V_2)
(V1, V2), and each side in the figure
(
i
,
j
)
(i,j)
(i,j) the points at both ends belong to these two subsets respectively
G
G
G is a bipartite graph
The related concepts of bipartite graph are as follows:
- Matching: a set with only edges. Any two edges in the set have no common points. Among all the matching of a graph, the matching with the largest number of edges is called the maximum matching of the graph
- Independent set: a set of nodes that are not connected to each other
- Edge coverage: any node is an edge set of at least one edge endpoint, that is, there are no isolated points
- Point coverage: a collection of points where any edge has at least one point, that is, there are no isolated edges
- Minimum path coverage: in a DAG, if there is a simple path set (vertex disjoint) and each vertex of the graph is on the path, the path is a path coverage, and the minimum path coverage is the path coverage with the least number of paths
Bipartite graph coloring
For a given graph, it is necessary to judge whether it is a bipartite graph before relevant operations can be carried out. For an undirected graph, it is a bipartite graph if and only if there is no ring composed of odd edges. This is a necessary and sufficient condition. For example, it is simply proved
As shown in the figure, when it is an odd ring, according to the definition of bipartite graph, you can see? Cannot be assigned at
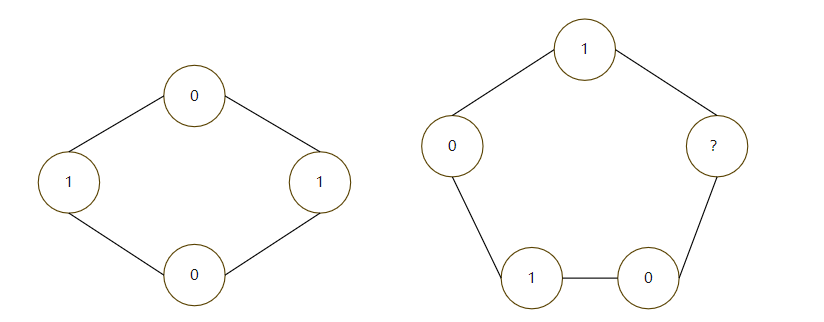
According to the nature of bipartite graph, all points are divided into two sets, so the two connected points must not belong to the same set. Therefore, starting from any point, set it to 1, and its adjacent point must be 0, and so on. If there is a point that cannot be assigned, it must not be bipartite graph, which can be realized by DFS
code
bool DFS(int u,int c)
{
col[u]=c;
for(int i=head[u];~i;i=e[i].next)
{
int v=e[i].to;
if(col[v]==col[u])return 0;
if(col[v]==-1&&!DFS(v,!col[u]))return 0;
}
return 1;
}
Of course, if the given graph is not a connected graph, you need to judge each non traversal point
for(int i=1;i<=n;i++) if(col[i]==-1)if(!DFS(i,1))return 0;
Bipartite graph correlation theorem
- K ö nig: minimum point coverage = maximum matching of bipartite graph
- Minimum edge coverage of bipartite graph: number of vertices - maximum matching of bipartite graph
- Minimum path coverage: number of vertices - maximum matching number of bipartite graph
- Maximum independent set: total number of points - maximum matching number of bipartite graph
To find the minimum path coverage set, you only need to output along the augmented path, and output all matching paths
code
void print(int u)
{
u+=n;//initialization
do
printf("%d ",u=u-n);
while(vis[u]=1,u=match[u]);
}
for(int i=1;i<=n;i++)
if(!vis[i])print(i);
Minimum intersectable path coverage: Floyd finding the transitive closure of the original graph
Maximum matching algorithm
Firstly, the concept of maximum matching is explained. Maximum matching refers to a group of matching with the largest number of edges in a bipartite graph. It is a kind of problem of bipartite graph. As shown in the figure, the matching relationship is given. Finding the maximum matching can convert the original graph into a maximum flow problem, add source points and sink points, set the edge weight to 1, and then run the maximum flow directly. The time complexity is
O
(
V
2
E
)
O(V^2E)
O(V2E), however, the graph given is a bipartite graph, which can be solved by using the properties of bipartite graph. The following are Hungarian algorithm and KM algorithm for solving by using the properties of bipartite graph
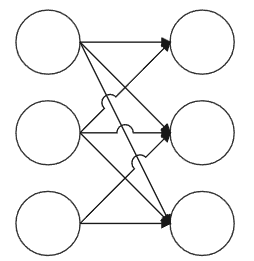

hungarian algorithm
Firstly, the concepts of alternating path and augmented path are given
Alternate path: starting from an unmatched point and passing through unmatched edge, matched edge, unmatched edge,... In turn, the path formed is an alternate path
Zengguang Road: starting from an unmatched point, take an alternate road. If you pass through another unmatched point different from the starting point, this alternate road is called Zengguang road
Note that the definition of augmented path in bipartite graph is different from that in solving maximum flow
An example is given to illustrate the simple algorithm idea. This is a simple legend and gives the matching relationship. Start from node 1 to find the matching point, 1 can find 4, and then 2 can find the matching point 5
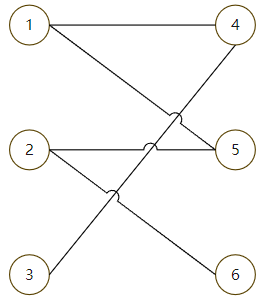
However, for node 3, its only matching point is 4. At this time, 4 has been matched with 1, so try to match 1 with other nodes
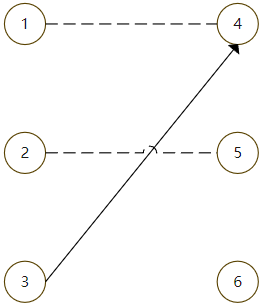
1 can match 5, but 5 already matches 2, so try to match 2 with other nodes

2 can match 6, so you can get the maximum matching result in the end
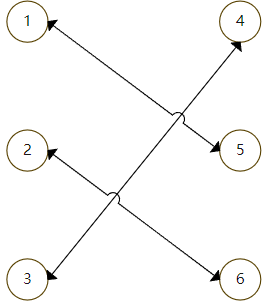
This is the basic idea of Hungarian algorithm. According to the concept, the existence of Zengguang road means that new matching can be added by modifying the current matching. The essence of Zengguang road is that the starting point and end point of a path are unpaired points. In the above process, the matching relationship sometimes needs to be changed from matched to unmatched. This operation is called "anti color", The match after "reverse color" is still legal and greater than or equal to the original match
Algorithm steps:
- Initialize the node and check from the first point $$in the left set
- inspect u u Adjacency point of u v v v. If v v If v does not match, match two points directly, otherwise from v v Start from the adjacency point of v to find Zengguang road. If Zengguang road exists, update the matching relationship, that is, reverse color, and then match u , v u,v u,v
- If the maximum match cannot be found, you can get a maximum match
code
bool maxmatch(int u) {//Incoming left collection node
for(int i=head[u]; ~i; i=e[i].next) {//BFS
int v=e[i].to;
if(!vis[v]) {//If you haven't visited
vis[v]=1;
if(!match[v]||maxmatch(match[v]))//If you can match
{
match[v]=u;//Set match
return 1;
}
}
}
return 0;
}
KM algorithm
The purpose of KM algorithm is to find the maximum weight perfect match of bipartite graph, that is, the size of two point sets of bipartite graph needs to be the same. Generally speaking, it is impossible to ensure that both sides of bipartite graph have the same size, so it is necessary to supplement points on one side with a small number of points, and then set the nonexistent edge weight to 0
Next are the concepts and theorems matching KM
Feasible top mark: give each node a point weight f ( i ) f(i) f(i), for all edges u − v u-v u − v, satisfy all edge weights w ( u , v ) ≤ f ( u ) + f ( v ) w(u,v)\le f(u)+f(v) w(u,v)≤f(u)+f(v)
Equivalent Subgraph: the generated subgraph of the original graph under a set of feasible top marks, including all points but only satisfying w ( u , v ) = f ( u ) + f ( v ) w(u,v)= f(u)+f(v) W (U, V) = the edge of F (U) + F (V) u − v u-v u−v
If an equal subgraph has a perfect match, it must be the maximum weight perfect match of the original graph
According to the theorem, in the process of solving the maximum weight perfect matching, it is necessary to constantly adjust the feasible vertex so that the equal subgraphs have perfect matching
It is impossible to determine all the top marks directly at the beginning, so it is necessary to confirm and modify the top marks repeatedly when one edge meets the requirements w ( u , v ) = f ( u ) + f ( v ) w(u,v)= f(u)+f(v) w(u,v)=f(u)+f(v), which means it is an edge of an equal subgraph. Add it to the graph
Let the top mark of the left point set of bipartite graph be l ( i ) l(i) l(i), the top mark of the right set is r ( i ) r(i) r(i), during initialization, because the feasible top standard needs to meet the point weight and greater than or equal to the edge weight, it may be set l ( i ) l(i) l(i) are all 0, r ( i ) r(i) r(i) is the maximum value of the edge weight connected to the corresponding point
In the process of adjusting the top mark, the purpose is to construct an equal subgraph, that is, constantly add new edges to the original subgraph, so that l ( i ) + r ( j ) = w ( i , j ) l(i)+r(j)=w(i,j) l(i)+r(j)=w(i,j), then you need to find an edge after initialization u − v u-v u − v makes u u u is not in the maximum matching of bipartite graph, but v v v in the maximum matching of bipartite graph (the weight of u point is 0 and the weight of v point is the maximum edge weight. In order to obtain the maximum matching, v is the benchmark matching by default)
For such an edge, we want to add it to the equal subgraph being constructed. If the edge satisfies the condition, the top mark sum needs to be reduced △ x = l ( u ) + r ( v ) − w ( u , v ) △x=l(u)+r(v)-w(u,v) △x=l(u)+r(v)−w(u,v)
Because default v v v in maximum matching, changing its point weight will affect other edges (such as the edge with the largest edge weight, if v v If the weight of point v is changed, the two ends of the edge with the largest edge weight may not meet the definition of feasible vertex), so only u u u to operate, that is l ( u ) + △ x l(u)+△x l(u) + △ x or r ( u ) − △ x r(u)-△x r(u)−△x( u u u is not necessarily on the left). In order to place and modify, some top marks do not meet the definition, so they are found every time △ x △x △ x as small as possible
Code (false) O ( n 3 ) O(n^3) O(n3))
bool maxmatch(int u) {
visr[u]=1;//
for(int i=1; i<=n; i++) {
if(visl[i])continue;
int d=l[i]+r[u]-gragh[u][i];//Get missing value
if(d==0) {//It means that this edge has satisfied the condition of equal subgraph
visl[u]=1;//Represents a possible match
if(!match[i]||maxmatch(match[i])) {
match[i]=u;
return 1;
}
} else delta[i]=min(delta[i],d);//Update minimum difference
}
return 0;
}
int KM() {
memset(match,0,sizeof(match));//Empty match
memset(l,0,sizeof(l));//Clear left point set
for(int i=1; i<=n; i++) {//Initialize the right top mark, which defaults to the maximum edge weight
r[i]=gragh[i][1];
for(int j=2; j<=n; j++)
r[i]=max(r[i],gragh[i][j]);
}
for(int i=1; i<=n; i++) {
for(int j=1; j<=n; j++)delta[j]=inf;
while(1) {
memset(visl,0,sizeof(visl));//Empty access
memset(visr,0,sizeof(visr));//ditto
if(maxmatch(i))break;
//If the representative i is not included and the match is not successful, the top mark needs to be adjusted
int d=inf;
for(int j=1; j<=n; j++)
if(!visl[j])d=min(d,delta[j]);
//visl[j] is 1, which means that it is already on the augmented road of the structure, and d is 0
//It is no longer possible to provide the difference that can increase the equal subgraph. Repeated fetching will cause an endless loop
for(int j=1; j<=n; j++) {
//It can be modified here because the matching failed
//That is, the top mark of the passing point cannot meet i within the maximum matching, so it needs to be modified
if(visr[j])r[j]-=d;
if(visl[j])l[j]+=d;
else delta[j]-=d;//Because r[j] increases, the difference becomes smaller
}
}
}
for(int i=1; i<=n; i++)res+=gragh[match[i]][i];//Cumulative sum matching edge
return res;
}
The worst complexity of bipartite graph matching is O ( n 2 ) O(n^2) O(n2) (maxpatch function), while the while(1) loop can be up to O ( n ) O(n) O(n) (try to construct matching with all nodes), so the complexity of the whole algorithm is the highest O ( n 4 ) O(n^4) O(n4)
It can be found that when modifying an edge, because the starting point of each DFS is the same, only one edge may be modified at a time. Therefore, if there is repeated search, changing DFS to BFS can reduce the repeatability and complexity of the search
Code( O ( n 3 ) O(n^3) O(n3))
int pre[maxn],match[maxn],delta[maxn],graph[maxn][maxn],n,m,res,l[maxn],r[maxn];
int a[maxn],p[maxn],b[maxn],c[maxn];
bool visl[maxn],visr[maxn];
void maxmatch(int u) {
int x,y=0,d,id=0;
memset(pre,0,sizeof(pre));//pre is used to record the previous edge
for(int i=1; i<=n; i++)delta[i]=inf;//Initialize right point set
match[y]=u;//Initialize matching relationship
while(1) {
x=match[y];
d=inf;//initialization
visr[y]=1;//visit
for(int i=1; i<=n; i++) {
if(visr[i])continue;
if(delta[i]>l[x]+r[i]-graph[x][i]) {//Can you add an edge x-i
delta[i]=l[x]+r[i]-graph[x][i];
pre[i]=y;//Connect an unmatched edge
}
if(delta[i]<d) {//Find a point with the least modification value
d=delta[i];//Record value
id=i;//Record number
}
}
for(int i=0; i<=n; i++)
if(visr[i])l[match[i]]-=d,r[i]+=d;//Try to modify
else delta[i]-=d;//The edge is not the shortest edge and may become the shortest edge after subtraction
y=id;
if(match[y]==-1)break;//Cannot continue matching
}
while(y) {//Construction matching
match[y]=match[pre[y]];
y=pre[y];
}
}
int KM() {
memset(match,-1,sizeof(match));//Empty match
memset(l,0,sizeof(l));
memset(r,0,sizeof(r));
for(int i=1; i<=n; i++) {
memset(visr,0,sizeof(visr));
maxmatch(i);//BFS left point set
}
for(int i=1; i<=n; i++)
if(match[i]!=-1)res+=graph[match[i]][i];
return res;
}
Bipartite graph game
Bipartite graph game is a kind of game model, which is related to the maximum matching of bipartite graph. Its basic model is as follows: given a bipartite graph and starting point, the two sides of the game operate in turn. Each time, they can only select the points adjacent to the last selected point, and can not select the points that have been visited, so the operator cannot continue to judge the negative
Let the starting point be S, there is a conclusion: if any maximum match of bipartite graph must have S, that is, S is the maximum matching point, then the first hand will win, otherwise the first hand will lose
Let's prove this conclusion
As shown in the figure, a maximum match is given. Assuming the starting point S=1, the first hand will choose 2 according to the strategy. At this time, the second hand will choose either no point or 3 (if 2-3 exists, this will be proved later). Then the first hand will choose from 3. It can be seen that as long as the first hand continues to choose according to the strategy of finding matching points, there will always be no point for the second hand in the end
If the starting point does not belong to the maximum matching, the first hand must lose, because the next step of the first hand from the starting point must be one of the matching points in the figure (later proved), then the situation is exactly the same as that in the previous paragraph, but the second hand chooses according to the strategy of matching points, and in the end, the first hand will always have no choice

Now let'S prove in more detail that if the maximum matching must include S, according to the previous statement, it is impossible for the backhand to select points other than the maximum matching, as shown in the figure. If the backhand can select non matching points, such as 9 in the figure, there will be more than one maximum matching scheme in the figure: 1-2,3-4,5-6,7-8 and 1-2,4-9,5-6,7-8 can be used as the maximum matching, Violation of the maximum match must include S

If the maximum matching does not necessarily include S, in this case, there may be a unique maximum matching, but S is not in the maximum matching, or S is not a necessary point for all maximum matching, as shown in the figure. Starting from 9, the next step must be the matching point, otherwise
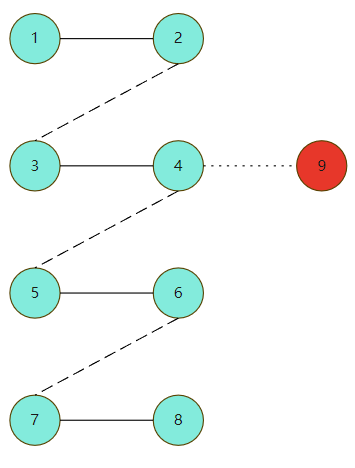
The situation shown in the figure below will appear. There is one edge 9-10 that does not belong to the maximum matching. Obviously, this is unreasonable, because 9 and 10 do not belong to the matching points, but they can form a matching. The original maximum matching is not the maximum, so there is a contradiction
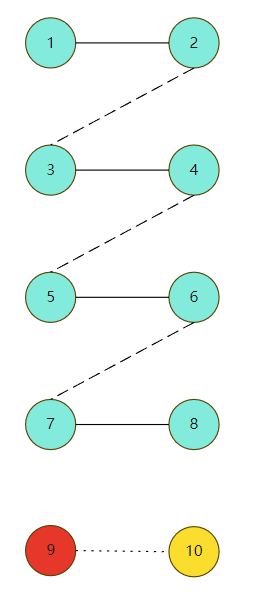
The next problem is how to determine whether the starting point belongs to the maximum matching. The method is very simple. Directly do the maximum matching for the original drawing with and without a starting point. If the matching number is the same, it means that the starting point is not necessarily in the maximum matching, otherwise it must be in the maximum matching, which can be solved by Dinic and Hungary
When running Dinic, you don't need to build a map twice according to whether there is a starting point. Instead, save the edge related to the starting point when building the map, and build the edge after running Dinic once to check whether Dinic increases traffic
To sum up, for the bipartite graph game, we can consider it in two major cases (actually one case, but the separation is clearer)
- Have a starting point
If there is a starting point, you need to judge whether the starting point must belong to the maximum matching, that is, the maximum matching must point. If so, the first hand will win, otherwise the first hand will lose - No starting point
If there is no starting point, the first hand needs to select the starting point. If the first hand selects the maximum matching point first, the second hand only needs to select the matching point of the corresponding maximum matching, the first hand will lose. If the picture is a complete matching, the first hand will select the maximum matching point. If it is not a complete matching, the first hand will select the non maximum matching point or the non essential point of the maximum matching, Then the second hand will always get the biggest match first, so the first hand can win
train
LuoguP1330
Main idea of the title: omitted
Idea: it can be seen from the problem design that river crabs cannot be connected. Then all river crabs can be divided into two sets, which just conforms to the bipartite graph. Then directly judge whether the given graph is a bipartite graph. If not, there is no solution. If not, select the nodes with less color. Because the problem does not guarantee connectivity, we should dye each connected block with bipartite graph
code
#include <iostream>
#include <queue>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=4e5+10;
int n,m,cnt,res,head[maxn/10],col[maxn/10],dress[2];
struct node {
int next,to;
} e[maxn<<1];
void Add(int from,int to) {
e[++cnt].to=to;
e[cnt].next=head[from];
head[from]=cnt;
}
bool DFS(int u,int c) {
col[u]=c;
dress[c]++;
for(int i=head[u]; ~i; i=e[i].next) {
int v=e[i].to;
if(col[v]==col[u])return 0;
if(col[v]==-1&&!DFS(v,!col[u]))return 0;
}
return 1;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >>n>>m;
memset(head,-1,sizeof(head));
memset(col,-1,sizeof(col));
while(m--) {
int u,v;
cin >>u>>v;
Add(u,v);
Add(v,u);
}
for(int i=1; i<=n; i++)
if(col[i]==-1) {
if(!DFS(i,1)) {
res=0;
break;
}
res+=min(dress[0],dress[1]);
dress[0]=dress[1]=0;
}
res==0? cout <<"Impossible": cout <<res;
return 0;
}
LuoguP1285
Main idea of the title: omitted
Idea: a very important point is that if two team members are not two-way, then these two people must not be in the same group. Therefore, when building the map, each point and the point of the same group must not build an edge. In this way, the whole graph can be divided into two point sets, that is, a bipartite graph. After coloring, the whole graph will be divided into multiple connected blocks with black and white. Obviously, Each block can only take all black or all white. In this way, the whole model can be abstracted into 01 knapsack model. There are k connected blocks. Each connected block can choose either black or white. It is required that the difference of the final grouping is the smallest. Here d p [ i ] [ j ] dp[i][j] dp[i][j] can be interpreted as whether j people can be selected on the ith connected block. See the code for the rest
code
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
int n,acc[121][2],pre[121][121],res,col[121],block,out[121];
bool gragh[121][121],dp[121][121],mark[121];
vector<int>path[121][2];
void DFS(int u,int f,int c) {
acc[block][col[u]=c]++;//Record the number of connected block colors c
path[block][c].push_back(u);//Record the color c of the connected block of the first block
for(int i=1; i<=n; i++)
if(!gragh[i][u]&&i!=f&&u!=i) {
if(col[i]==-1)DFS(i,u,c^1);//If the adjacent points are not stained, take the opposite color
else if(col[i]==c) {
cout <<"No solution";
exit(0);
}
}
}
int main() {
cin >>n;
memset(col,-1,sizeof(col));
for(int i=1; i<=n; i++) {
int k;
while(cin >>k&&k)gragh[i][k]=1;
}
for(int i=1; i<=n; i++)
for(int j=i+1; j<=n; j++)
if(gragh[i][j]!=gragh[j][i])gragh[i][j]=gragh[j][i]=0;
//If you can't reach each other, don't connect the edges
for(int i=1; i<=n; i++)
if(col[i]==-1) {//Not dyed
block++;
DFS(i,0,1);
}
dp[0][0]=1;//initialization
for(int i=1; i<=block; i++)//Multiple connected blocks can be equivalent to block items
for(int j=0; j<=n/2; j++) {//capacity
int p=j-acc[i][0];//acc[i][0] is the number of 0 that can be taken out of the first I connected blocks, and p is the number required to reach j
if(p>=0&&dp[i-1][p])dp[i][j]=1,pre[i][j]=0;
//If more zeros are needed and the first i-1 blocks are available, it means that the current installed j blocks can also be met
//pre records the previous transfer status and installs 0
p=j-acc[i][1];//
if(p>=0&&dp[i-1][p])dp[i][j]=1,pre[i][j]=1;
//ditto
}
for(int i=n/2; i>=0; i--)
if(dp[block][i]) {//There is a solution that makes the capacity difference small
res=i;
break;
}
int t=res;
for(int i=block; i>0; i--) {//Traverse each block and backtrack the solution
for(int j=0; j<path[i][pre[i][t]].size(); j++)
//Traverse the block and enter the node with color pre[i][t]
mark[out[++out[0]]=path[i][pre[i][t]][j]]=1;
t-=acc[i][pre[i][t]];//Subtract the number of blocks that have been used
}
sort(out+1,out+out[0]+1);//Sort the output according to the meaning of the question
cout <<out[0]<<" ";
for(int i=1; i<=out[0]; i++)
cout <<out[i]<<" ";
cout <<endl<<n-out[0]<<" ";
for(int i=1; i<=n; i++)
if(!mark[i])cout <<i<<" ";
return 0;
}
POJ1274
Main idea of the title: there is a direct corresponding relationship between cowshed and cattle. Each cow has its own preference for cowshed. A cowshed can only be allocated to one cow, and a cow can only be allocated to one cowshed. Calculate the maximum number of cows that can be allocated to the cowshed
Idea: for the bipartite graph problem, construct the bipartite graph according to the corresponding relationship, and then use the Hungarian algorithm to calculate the maximum matching
code
#include <iostream>
#include <queue>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=4e4+10;
int n,m,cnt,head[500],match[500];
struct node {
int next,to;
} e[maxn<<1];
void Add(int from,int to) {
e[++cnt].to=to;
e[cnt].next=head[from];
head[from]=cnt;
}
bool vis[500];
bool maxmatch(int u) {//Incoming left collection node
for(int i=head[u]; ~i; i=e[i].next) {//BFS
int v=e[i].to;
if(!vis[v]) {//If you haven't visited
vis[v]=1;
if(!match[v]||maxmatch(match[v]))//If you can match
{
match[v]=u;//Set match
return 1;
}
}
}
return 0;
}
int main() {
while(~scanf("%d%d",&n,&m)) {
int res=0;
memset(head,-1,sizeof(head));
memset(match,0,sizeof(match));
cnt=0;
for(int i=1; i<=n; i++) {
int s;
scanf("%d",&s);
while(s--) {
int x;
scanf("%d",&x);
Add(i,x+n);
//Add(x+n,i); There is no need to build a bilateral relationship here, because after the matching relationship is determined, it can be deduced according to the matching
}
}
for(int i=1; i<=n; i++) {
memset(vis,0,sizeof(vis));
if(maxmatch(i))res++;
}
printf("%d\n",res);
}
return 0;
}
POJ1325
Give two machines A, B, A have N working modes (0~ n-1) and B have m working modes (0~ m-1). At first, they all work in working mode 0. Now, given k jobs, each job triple constraint is given ( i , x , y ) (i,x,y) (i,x,y) indicates that it can be processed with X on A or Y on B. to complete the work, it is necessary to restart to modify the machine working mode. It is necessary to arrange the sequence of work and allocate appropriate machines to minimize the number of restarts and output
Idea: at the beginning, it works in working mode 0, so it can be ignored in working formula 0. Finding the minimum restart times is equivalent to finding the minimum point coverage of bipartite graph and the maximum matching. Just run Hungarian algorithm
code
#include <iostream>
#include <queue>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=4e4+10;
int n,m,cnt,k,head[500],match[500];
struct node {
int next,to;
} e[maxn<<1];
void Add(int from,int to) {
e[++cnt].to=to;
e[cnt].next=head[from];
head[from]=cnt;
}
bool vis[500];
bool maxmatch(int u) {//Incoming left collection node
for(int i=head[u]; ~i; i=e[i].next) {//BFS
int v=e[i].to;
if(!vis[v]) {//If you haven't visited
vis[v]=1;
if(!match[v]||maxmatch(match[v])) { //If you can match
match[v]=u;//Set match
return 1;
}
}
}
return 0;
}
int main() {
while(~scanf("%d",&n)&&n) {
scanf("%d%d",&m,&k);
int res=0;
memset(head,-1,sizeof(head));
memset(match,0,sizeof(match));
cnt=0;
while(k--) {
int i,x,y;
scanf("%d%d%d",&i,&x,&y);
if(x==0||y==0)continue;//Skip working mode 0
Add(x,y+n);
}
for(int i=0; i<n; i++) {
memset(vis,0,sizeof(vis));
if(maxmatch(i))res++;
}
printf("%d\n",res);
}
return 0;
}
LuoguP1263
Main idea of the title: omitted
Idea: if there is no wall, treat each row as a left set and column as a right set. For the open space, connect the row and column, but the wall separates the rows and columns. Therefore, it is necessary to treat the connected blocks generated by the separation as separate individuals, that is, modify the traversal range. See the code for details
code
#include <bits/stdc++.h>
using namespace std;
const int maxn=2e4+10;
int m,n,cnt,maze[250][250],match[maxn],head[maxn],res,acch,accz;
int col[maxn],parth[250][250],partz[250][250];
bool vis[maxn];
struct node {
int next,to;
} e[maxn<<1];
void Add(int from,int to) {//Chain forward star
e[++cnt].next=head[from];
e[cnt].to=to;
head[from]=cnt;
}
bool maxmatch(int u) {//Maximum match
for(int i=head[u]; ~i; i=e[i].next) {
int v=e[i].to;
if(!vis[v]) {
vis[v]=1;
if(!match[v]||maxmatch(match[v])) {
match[v]=u;
return 1;
}
}
}
return 0;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >>n>>m;
memset(head,-1,sizeof(head));
memset(col,-1,sizeof(col));
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
cin >>maze[i][j];
for(int i=1; i<=n; i++)maze[i][0]=2;//Processing boundary values
for(int i=1; i<=m; i++)maze[0][i]=2;//ditto
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
if(maze[i][j]<2) {//If it's not a wall
if(maze[i][j-1]>1)parth[i][j]=++acch;//The previous point is the wall, creating a new connected block
else parth[i][j]=parth[i][j-1];//Not walls, merge connected blocks
}
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
if(maze[i][j]<2) {
if(maze[i-1][j]>1)partz[i][j]=++accz;//The previous point is the wall, creating a new connected block
else partz[i][j]=partz[i-1][j];//Not walls, merge connected blocks
}
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
if(maze[i][j]==0)Add(parth[i][j],partz[i][j]);//If it is an open space, build sides on the left and right
for(int i=1; i<=acch; i++) {//Traverse each column connected block
for(int j=1; j<=accz; j++)vis[j]=0;
res+=maxmatch(i);//Statistical matching quantity
}
cout <<res<<endl;
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)//The match array records all matching edges
if(maze[i][j]==0&&parth[i][j]==match[partz[i][j]])cout <<i<<" "<<j<<endl;
//Open space, and the row corresponds to the column?
return 0;
}
2019icpc Nanjing J
Main idea of the title: omitted
Idea: KM template questions, but need to use real ones O ( n 3 ) O(n^3) O(n3) template
code
#include <bits/stdc++.h>
#define int long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=512;
int pre[maxn],match[maxn],delta[maxn],graph[maxn][maxn],n,res,l[maxn],r[maxn];
int a[maxn],p[maxn],b[maxn],c[maxn];
bool visl[maxn],visr[maxn];
void maxmatch(int u) {
int x,y=0,d,id=0;
memset(pre,0,sizeof(pre));//pre is used to record the previous edge
for(int i=1; i<=n; i++)delta[i]=inf;//Initialize right point set
match[y]=u;//Initialize matching relationship
while(1) {
x=match[y];
d=inf;//initialization
visr[y]=1;//visit
for(int i=1; i<=n; i++) {
if(visr[i])continue;
if(delta[i]>l[x]+r[i]-graph[x][i]) {//Can you add an edge x-i
delta[i]=l[x]+r[i]-graph[x][i];
pre[i]=y;//Connect an unmatched edge
}
if(delta[i]<d) {//Find a point with the least modification value
d=delta[i];//Record value
id=i;//Record number
}
}
for(int i=0; i<=n; i++)
if(visr[i])l[match[i]]-=d,r[i]+=d;//Try to modify
else delta[i]-=d;//The edge is not the shortest edge and may become the shortest edge after subtraction
y=id;
if(match[y]==-1)break;//Cannot continue matching
}
while(y) {//Construction matching
match[y]=match[pre[y]];
y=pre[y];
}
}
int KM() {
memset(match,-1,sizeof(match));//Empty match
memset(l,0,sizeof(l));
memset(r,0,sizeof(r));
for(int i=1; i<=n; i++) {
memset(visr,0,sizeof(visr));
maxmatch(i);//BFS left point set
}
for(int i=1; i<=n; i++)
if(match[i]!=-1)res+=graph[match[i]][i];
return res;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >>n;
for(int i=1; i<=n; i++)cin >>a[i];
for(int i=1; i<=n; i++)cin >>p[i];
for(int i=1; i<=n; i++)cin >>b[i];
for(int i=1; i<=n; i++)cin >>c[i];
//Data entry
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
for(int k=1; k<=n; k++)
if(b[i]+c[j]>a[k])graph[i][j]+=p[k];//If you can defeat, build an edge
cout <<KM();
return 0;
}
/*
4
1 2 3 4
1 1 1 1
0 0 1 1
0 1 1 2
*/
LuoguP6577
Main idea of the title: omitted
Train of thought: KM template question
code
#include <bits/stdc++.h>
#define int long long
#define inf 1e18 / / Infinity 0x3f3f3f is smaller here
using namespace std;
const int maxn=512;
int pre[maxn],match[maxn],delta[maxn],graph[maxn][maxn],n,m,res,l[maxn],r[maxn];
int a[maxn],p[maxn],b[maxn],c[maxn];
bool visl[maxn],visr[maxn];
void maxmatch(int u) {
int x,y=0,d,id=0;
memset(pre,0,sizeof(pre));//pre is used to record the previous edge
for(int i=1; i<=n; i++)delta[i]=inf;//Initialize right point set
match[y]=u;//Initialize matching relationship
while(1) {
x=match[y];
d=inf;//initialization
visr[y]=1;//visit
for(int i=1; i<=n; i++) {
if(visr[i])continue;
if(delta[i]>l[x]+r[i]-graph[x][i]) {//Can you add an edge x-i
delta[i]=l[x]+r[i]-graph[x][i];
pre[i]=y;//Connect an unmatched edge
}
if(delta[i]<d) {//Find a point with the least modification value
d=delta[i];//Record value
id=i;//Record number
}
}
for(int i=0; i<=n; i++)
if(visr[i])l[match[i]]-=d,r[i]+=d;//Try to modify
else delta[i]-=d;//The edge is not the shortest edge and may become the shortest edge after subtraction
y=id;
if(match[y]==-1)break;//Cannot continue matching
}
while(y) {//Construction matching
match[y]=match[pre[y]];
y=pre[y];
}
}
int KM() {
memset(match,-1,sizeof(match));//Empty match
memset(l,0,sizeof(l));
memset(r,0,sizeof(r));
for(int i=1; i<=n; i++) {
memset(visr,0,sizeof(visr));
maxmatch(i);//BFS left point set
}
for(int i=1; i<=n; i++)
if(match[i]!=-1)res+=graph[match[i]][i];
return res;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >>n>>m;
for(int i=1; i<=n; i++)//Note initialization
for(int j=1; j<=n; j++)
graph[i][j]=-inf;
while(m--) {
int x,y,w;
cin >>x>>y>>w;
graph[x][y]=w;
}
cout <<KM()<<endl;
for(int i=1; i<=n; i++)
cout <<match[i]<<" ";
return 0;
}
LuoguP4014
Main idea of the title: omitted
Idea: the maximum total income is directly solved by KM. The minimum income needs to reverse the edge weight and then run KM. After running, reverse the result
code
#include <bits/stdc++.h>
#define int long long
#define inf 1e18
using namespace std;
const int maxn=512;
int pre[maxn],match[maxn],delta[maxn],graph[maxn][maxn],n,m,res,l[maxn],r[maxn];
bool visl[maxn],visr[maxn];
void maxmatch(int u) {
int x,y=0,d,id=0;
memset(pre,0,sizeof(pre));//pre is used to record the previous edge
for(int i=1; i<=n; i++)delta[i]=inf;//Initialize right point set
match[y]=u;//Initialize matching relationship
while(1) {
x=match[y];
d=inf;//initialization
visr[y]=1;//visit
for(int i=1; i<=n; i++) {
if(visr[i])continue;
if(delta[i]>l[x]+r[i]-graph[x][i]) {//Can you add an edge x-i
delta[i]=l[x]+r[i]-graph[x][i];
pre[i]=y;//Connect an unmatched edge
}
if(delta[i]<d) {//Find a point with the least modification value
d=delta[i];//Record value
id=i;//Record number
}
}
for(int i=0; i<=n; i++)
if(visr[i])l[match[i]]-=d,r[i]+=d;//Try to modify
else delta[i]-=d;//The edge is not the shortest edge and may become the shortest edge after subtraction
y=id;
if(match[y]==-1)break;//Cannot continue matching
}
while(y) {//Construction matching
match[y]=match[pre[y]];
y=pre[y];
}
}
int KM() {
memset(match,-1,sizeof(match));//Empty match
memset(l,0,sizeof(l));
memset(r,0,sizeof(r));
for(int i=1; i<=n; i++) {
memset(visr,0,sizeof(visr));
maxmatch(i);//BFS left point set
}
for(int i=1; i<=n; i++)
if(match[i]!=-1)res+=graph[match[i]][i];
return res;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >>n;
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
cin >>graph[i][j];
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
graph[i][j]*=-1;
cout <<-KM()<<endl;
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
graph[i][j]*=-1;
res=0;
cout <<KM()<<endl;
return 0;
}
LuoguP1971
Main idea of the title: omitted
Idea: using the idea of relative displacement, the movement of chess pieces is regarded as the movement of spaces. Then the space is first moved to white, which is similar to the nature of sunspots. Therefore, the space is regarded as black, so the whole maze can be transformed into the problem of pairwise matching between black and white, black and white coloring, building a bipartite graph, and according to the idea of bipartite graph game, Judge whether the current moving point position is the maximum matching point before moving. If so, the current hand must win, otherwise it must lose
Judge whether the current point position is the required point for maximum matching. You can delete the point from the graph and delete the original matching relationship to see whether another point of the original matching relationship can form another maximum matching. If yes, it means that the current point is not a required point, then the current hand must be input (according to the optimal strategy), because the current hand must enter the maximum matching in the next step, Record whether the current hand of each step must lose and win. Judge whether the first hand is wrong at the beginning. You need to judge whether the first hand must win in the k round, and the second hand must win after the next round, that is, both states are 1, which means that the first hand of this step is wrong. Record it
code
#include <bits/stdc++.h>
using namespace std;
const int maxn=5e3+10;
int n,m,k,sx,sy,cnt,head[maxn],match[maxn];
vector<int>res;
char maze[50][50];
bool color[50][50],vis[maxn/2],block[maxn/2],win[maxn/2];
struct node {
int next,to;
} e[maxn];
void Add(int from,int to) {//Chain forward star
e[++cnt].to=to;
e[cnt].next=head[from];
head[from]=cnt;
}
int Hash(int i,int j) {//Discrete coordinates
return (i-1)*m+j;
}
bool maxmatch(int u) {
for(int i=head[u]; ~i; i=e[i].next) {
int v=e[i].to;
if(block[v])continue;//This point has been removed
if(!vis[v]) {
vis[v]=1;
if(!match[v]||maxmatch(match[v])) {
match[v]=u;
match[u]=v;
return 1;
}
}
}
return 0;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >>n>>m;
memset(head,-1,sizeof(head));
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++) {
cin >>maze[i][j];
if(maze[i][j]=='.')//Storage starting point
sx=i,sy=j;
else if(maze[i][j]=='O')//Mark white dots
color[i][j]=1;
}
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
if(color[i][j]) {
if(i+1<=n&&!color[i+1][j]) {//Jianbian
Add(Hash(i,j),Hash(i+1,j));
Add(Hash(i+1,j),Hash(i,j));
}
if(j+1<=m&&!color[i][j+1]) {
Add(Hash(i,j+1),Hash(i,j));
Add(Hash(i,j),Hash(i,j+1));
}
if(i>1&&!color[i-1][j]) {//Jianbian
Add(Hash(i,j),Hash(i-1,j));
Add(Hash(i-1,j),Hash(i,j));
}
if(j>1&&!color[i][j-1]) {//Jianbian
Add(Hash(i,j),Hash(i,j-1));
Add(Hash(i,j-1),Hash(i,j));
}
}
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
if(color[i][j]&&!match[Hash(i,j)]) {//Edge construction based on white dots
memset(vis,0,sizeof(vis));
maxmatch(Hash(i,j));//matching
}
cin >>k;
for(int i=1; i<=2*k; i++) {
int id=Hash(sx,sy);
block[id]=1;//It means that this one has been accessed and cannot be used as a match
if(match[id]==0)//This is a non necessary / non matching point. The next step must be at the matching point, and the next person must win
win[i]=0;
else {
int t=match[id];//t will not match the id because it is already marked on the block
match[id]=match[t]=0;
memset(vis,0,sizeof(vis));
if(maxmatch(t))win[i]=0;
else win[i]=1;
//Try to remove the id and start matching. If there is still a maximum matching, the id is a non mandatory point
//The non essential point is the starting point. The next person must be at the matching point and the next person must win
}
cin >>sx>>sy;//Enter next operation
}
for(int i=1; i<=k; i++)
if(win[2*i-1]&&win[2*i])//If A could have won, but B won after the game, it means A made A mistake
res.push_back(i);
int len=res.size();
cout <<len<<endl;
for(int i=0; i<len; i++)
cout <<res[i]<<endl;
return 0;
}
LuoguP4055
Main idea of the title: omitted
Idea: first of all, make a statement:
There is a problem with the data! There is a problem with the data! There is a problem with the data!
The data ignores data similar to the following two types
3 3 3 3 .## .## .## .## ..# #..
Therefore, part of the problem solution on Luogu may be right, but the code is logically wrong. I can't guarantee that the code given below is right, because there is no more comprehensive data
Here is the idea
According to the meaning of the question, the adjacent feasible lattice can obviously connect edges. Then the whole feasible domain is divided into black and white parts by using the black-and-white coloring method. In this way, a bipartite graph can be constructed, and the question will be transformed into a bipartite graph game. However, the first hand of this question is to select the point first, not from the starting point
In order to win the first hand, the first hand needs to make the current point as the starting point of the maximum matching after the second hand goes, which is consistent with the model of bipartite graph game. Then the point that the first hand needs to find is connected with the maximum matching, but it can not belong to the maximum matching point. If the whole graph is completely matched, there is obviously no such point
There may be multiple maximum matches. If the first player takes a necessary point for the maximum match, it is obvious that the second player will start from the "starting point" in the game model, and the first player will lose. Therefore, the first player needs to take all points that are not necessary for the maximum match
In order to find all the necessary points with the largest matching, you can start the search from one non essential point. Assuming that its color is black, if you can find black through a white point search, the other black point must also be non essential point. Because these two points are equivalent, the edge composed of them and common points can replace the one with the largest matching edge in the original image, and you can try to draw a picture
code
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,m,match[maxn],head[maxn],cnt,ans,res,color[maxn];
int point[1212][1212];
char maze[1212][1212];
bool vis[maxn],une[maxn];
struct node {
int next,to;
} e[maxn];
void Add(int from,int to) {
e[++cnt].to=to;
e[cnt].next=head[from];
head[from]=cnt;
}
bool maxmatch(int u) {
for(int i=head[u]; ~i; i=e[i].next) {
int v=e[i].to;
if(!vis[v]) {
vis[v]=1;
if(match[v]==-1||maxmatch(match[v])) {
match[v]=u;
return 1;
}
}
}
return 0;
}
void DFS(int u) {
if(une[u])return ;
une[u]=1;
for(int i=head[u]; ~i; i=e[i].next) {
int v=e[i].to;
if(match[v]!=-1)
DFS(match[v]);
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >>n>>m;
memset(match,-1,sizeof(match));
memset(head,-1,sizeof(head));
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
cin >>maze[i][j];
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
if(maze[i][j]=='.') {
point[i][j]=++ans;//Discretization
if((i+j)%2==0)color[ans]=1;//Dyeing, a little skill
//Only even numbers and lattices are dyed, which can ensure that odd numbers and lattices must be 0
}
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
if(maze[i][j]=='.') {//Mapping
if(point[i+1][j]) {//Use the coordinates that have been discretized to replace
Add(point[i][j],point[i+1][j]);
Add(point[i+1][j],point[i][j]);
}
if(point[i][j+1]) {
Add(point[i][j],point[i][j+1]);
Add(point[i][j+1],point[i][j]);
}
}
for(int i=1; i<=ans; i++)//Construct maximum match
if(color[i]) {//Based on black spots
memset(vis,0,sizeof(vis));
if(match[i]==-1)
res+=maxmatch(i);
}
if(cnt/2==res||(ans/2==res&&cnt/2+1==ans)) {//Is there no solution to the special judgment
cout <<"LOSE"<<endl;
return 0;
}
cout <<"WIN"<<endl;
for(int i=1; i<=ans; i++)//Anti marking, indicating that it has been on the maximum match
if(match[i]!=-1)match[match[i]]=i;
for(int i=1; i<=ans; i++)if(match[i]==-1)DFS(i);
//If it is a non essential point, find another non essential point
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
if(une[point[i][j]])//Judge whether it is an unnecessary point according to the discrete coordinates
cout <<i<<" "<<j<<endl;
return 0;
}
/*
3 3
.##
.##
..#
*/
summary
The most basic knowledge points of a bipartite graph are maximum matching and coloring. The rest of the knowledge points are extended on these two points, which need a deep understanding. As can be seen from LuoguP1285, a bipartite graph can turn the whole graph into connected blocks with dual properties. If these connected blocks are nested into the knapsack model, the problem can be solved with the idea of DP, This is very ingenious
Bipartite graph, to be exact, is a kind of thought, a kind of thinking. We need to master how to convert the problem into a bipartite graph and how to apply the bipartite graph model to solve the problem
KM algorithm is an extension of maximum matching. To be exact, it uses the top mark and edge weight to restrict the value. By constantly modifying the top mark, it indirectly modifies the edge and matching relationship, and finally obtains the maximum weight matching
Most of the problems of bipartite graph can be solved by other algorithms of network flow, but due to the particularity of bipartite graph, the related algorithms of bipartite graph are more suitable for their own problems
reference
- AHA algorithm
- Graph theory -- bipartite graph
- Algorithm training camp: massive diagrams + competition questions
- Bipartite graph learning notes
- 2019 Zhejiang Normal University Summer ACM training lecture 2 Graph Theory (II) bipartite graph and network flow
- "Bipartite graph" learning notes
- P1285 team member grouping problem solving
- P1263 [CEOI2002] Royal guards
- Bipartite graph of August 16 of 2020ICPC summer training in Tongji University and its application
- Algorithm learning notes (74): bipartite graph game
- Explanation and proof of bipartite graph game algorithm (learning notes of summer 21)
- 1971 rabbit and egg problem solution