view and reshape operations

The functions and usage of the two are the same, but it is necessary to ensure that the overall size of the view remains unchanged, that is, numel () is consistent

view operation will lose dimension information. Remember the storage order of data

a = torch.rand(4,1,28,28)
b = a.view(4,28*28)     #Two dimensions are missing
print(b)
print(b.shape)
c = a.view(4*28,28)     #Two dimensions are missing
d = a.view(4*1,28,28)   #A dimension is missing

e = a.reshape(4*1,28,28)        #Same as view
print(c.shape)
print(d.shape)
print(e.shape)

Squeeze and Unsqueeze

Extrusion and unfolding

 unsqueeze

Inserting a new dimension will not change the data itself, increase or decrease the data, which is equivalent to adding a group

a = torch.rand(4,1,28,28)
b = a.unsqueeze(0)      #Add dimension 1 before dimension 0
c = a.unsqueeze(4)      #Add dimension 1 before dimension 4
d = a.unsqueeze(-1)     #Add 1 dimension after the last dimension
e = a.unsqueeze(-4)
f  = a.unsqueeze(-5)
print(b.shape),print(c.shape),print(d.shape)
print(e.shape),print(f.shape)

It can also change the shape of the tensor

a = torch.tensor([1,2])
b = a.unsqueeze(0)      #Add a dimension outside
c = a.unsqueeze(1)      #Add a dimension to it

print(a)
print(a.shape)
print(b)
print(c)

It can also nest multiple ~ expansion dimensions

#a = torch.rand(4,1,28,30)  #You can use unsqueeze to expand a d into 3D, and then expand it into a

a = torch.rand(28)
b = a.unsqueeze(0)
c = a.unsqueeze(0).unsqueeze(0)
d = a.unsqueeze(0).unsqueeze(0).unsqueeze(3)
print(b.shape),print(c.shape),print(d.shape)

 

squeeze

Extrusion, as the name suggests, is dimension deletion

Positive and negative indexes can be received. If the number of the current index is 1, this dimension will be removed, otherwise it will remain unchanged,

If the index is not given, all qualified indexes will be removed by default

a = torch.rand(1,32,1,1)
b = a.squeeze()      #Do not write anything. Delete all size 1 by default
c = a.squeeze(0)    #If the index position is 1, remove this dimension, otherwise it remains unchanged
d = a.squeeze(1)    #unchanged
e = a.squeeze(-1)
print(b.shape),print(c.shape)
print(d.shape),print(e.shape)

expand and repeat

Both can extend a tensor shape, which is equivalent. However, repeat has disadvantages. expand is recommended

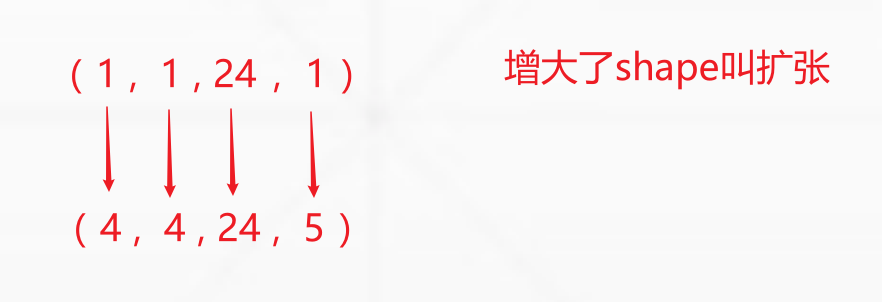
expand

It will not actively copy data, which is fast and saves memory

Its expansion has two conditions

1. Only when the current dimension size is 1 can it be expanded arbitrarily, otherwise it cannot be expanded.

2. The dimensions remain unchanged before and after expansion

#   a = torch.rand(4,32,14,14)
b = torch.rand(1,32,1,1)    #Next, expand from b to a
ba = b.expand(4,32,14,14)
print(ba.shape)
c = b.expand(-1,-1,4,14)    #Enter - 1 to return the original corresponding data
print(c.shape)

repeat 

repeat () the parameter it gives is no longer the expanded data, but the number of times each dimension needs to be repeated. The original data will be changed

Two conditions:

1. The dimension remains unchanged

2. The given parameter is the number of repetitions of each dimension, which should be calculated by yourself

a = torch.rand(1,12,1,1)
b = a.repeat(4,12,8,13)         #Number of times to repeat each dimension
c = a.repeat(4,1,12,12)
print(b.shape)
print(c.shape)

.t                transpose                permute

Three dimension conversion operations

. t # transpose operation

This method is only applicable to two dimensions, that is, matrix

a = torch.randn(2,4)
b = a.t()
print(a),print(b)

Transfer dimension exchange

After the dimension transformation operations such as transfer and permute, the tensor is no longer stored continuously in memory, while the view operation requires the memory of tensor to be stored continuously. Therefore, a contiguous copy needs to be returned

view will blur the dimension order relationship and need to be tracked manually

a = torch.rand(4,3,32,32)
b = a.transpose(1,3)        #Represents the dimension to be exchanged
print(b.shape)

a1 = a.transpose(1,3).contiguous().view(4,3*32*32).view(4,3,32,32)  #The first dimension is exchanged but not exchanged back. Even if the shape is the same, it is actually different
a2 = a.transpose(1,3).contiguous().view(4,3*32*32).view(4,32,32,3).transpose(1,3)#Remember the order after view. You have to change it back

print(a1.shape),print(a2.shape)
print(torch.all(torch.eq(a,a1)))       #Judge whether the content remains unchanged
print(torch.all(torch.eq(a,a2)))        #The eq function compares whether the contents are consistent. all returns TRUE or FALSE

permute exchange dimension

It can complete the exchange of any dimension, which is equivalent to calling any number of transfers

permute() use

Use the position where the index of the original shape is placed to determine who exchanges with whom

a = torch.rand(4,3,28,28)
b = a.transpose(1,3).transpose(0,2)
p = a.permute(2,3,0,1)  #One step in place
print(b.shape)
print(p.shape)