Definition from Wikipedia

The travelling salesman problem (also called the travelling salesperson problem or TSP) asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?"

Recently, in order to study the paper of Kool boss, we used neural network to guide dynamic programming to solve TSP, so we planned to do this idea by ourselves. Anyway, no matter where the neural network is used, write the dp first, and then the beautiful Ma Zhengqi starts to search the whole network and sort out the code... In order to save my time, I will explain only a few key parts below. For the basic process of dp, please refer to the links in Reference.

I use 0, 1, N - 1 is used to number n cities. The comparison revolves around the following group of correspondence:

Of course, it's OK for the city number to be from 1 to N, but those who are so lazy as sister Zhengqi certainly didn't study it. Just number it from 0 to N-1 and explain the corresponding relationships of these groups

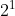• The first two lines are the relationship between decimal and corresponding binary bits. For example, binary number 1 corresponds to decimal number, binary number 10 corresponds to decimal number, binary number 11 corresponds to decimal number.
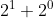• Their relationship with shift operation is that binary number 1 corresponds to decimal number, the same value can be obtained by using the shift operation 1 < < 0. The corresponding relationship between decimal number and shift is: power is the number to be shifted, for example, 1 < < (k-1) is decimal.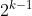
• The last three digits of the set of cities defined by 1-1 can be used to indicate whether there is a binary number of cities from 1 to 1. Therefore, it has nothing to do with whether the last three digits of the set of cities defined by me will always appear in the binary number of cities from 1 to 1.

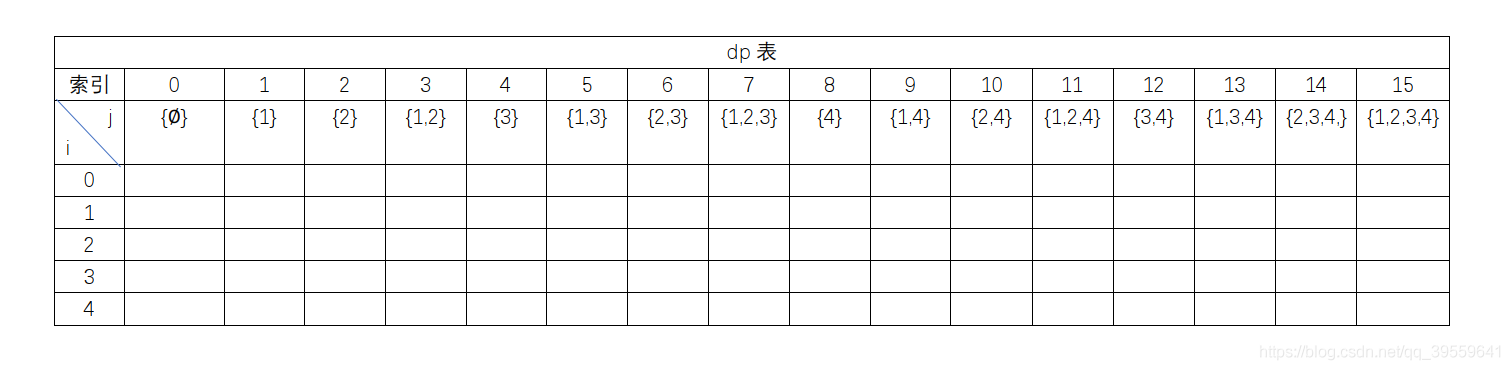
The above figure is copied from the Reference link. The table shows the situation of dp[i][j]. The "index" row is the decimal value of j, and the lower row set is the set represented by this value. For example, when j is 0, each bit in its binary is 0, that is, all cities are not in the set represented, so it is an empty set. When j is 1, only the last binary is 1, that is, only city 1 in the set, and when j is 3, its binary is 11, so city 1 and city 2 are in the set, when j is 4, the binary is 100, and only city 3 is in the set.

By analogy, when the set represented by j is the largest, that is, cities 1 to n-1 are in the set. At this time, the N-1 bits in the binary of j are all 1, and the corresponding decimal value is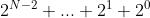. From the corresponding graph, we can see that the corresponding bit weight of city N-1 is, that is, its decimal value, which is specially listed in the corresponding relationship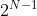One, the significance of which is that we calculate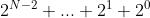A skill often used in:

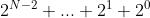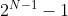•  = The corresponding binary is 111 = 1000 - 1. When all binary bits are 1, it is troublesome to add one bit by one according to the bit weight. The usual practice is to first calculate the decimal value of the number 1 larger than it, and then subtract 1. Then according to the corresponding relationship between decimal and shift,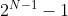This value can be calculated by (1 < < (n-1)) - 1.

Shape pressure dp needs to switch back and forth between binary and decimal, which involves the city number corresponding to binary and the calculation of decimal value by shift operation. We should clarify the relationship between them before continuing.

After the correspondence between them is determined, let's look at the core part: dp[i][j] the calculation of this array.

dp[i][j]: starting from city I, passing through each city in the set represented by j only once, and then returning to the shortest path length of city 0

Here we start from city 0 by default and then return to city 0, so we have the above definition dp[i][j]. Where dp[0][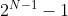]The meaning of dp[i][j] is the shortest path length starting from city 0, passing through city 1 to N-1, and then returning to city 0. When city I is included in the set represented by j, dp[i][j] is meaningless, because TSP stipulates that each city is visited only once, and starting from I and then passing through I is visited twice, so it is meaningless. When writing code, we skip such positions in the array. dp[i][0] represents the shortest path length from city I through empty set to city 0, that is, the length of edge I - > 0. Before starting dp, we first fill in the value of dp[i][0], and the subsequent dp[i][j] needs to be calculated according to them.

The following three for loops are the core part. The first two sides traverse I and j, and DP [i] [J] should be filled in by column. Because the later columns need to be calculated according to the previous columns, I is responsible for traversing N cities from 0 to N-1 in the inner layer, while J is responsible for traversing the set represented by J. the empty set of the set has been filled in during initialization. Here, only the maximum value of 1 to j needs to be traversed. The maximum value of J should be (1 < < (N-1)) - 1. We define the variable m as (1 < < (N-1)), because the range is closed on the left and open on the right, and M is 1 larger than the maximum value to be traversed. In addition, in these two-layer loops, we skip the case that I is included in the set represented by J, which can be represented by (J > > (I - 1)) & 1 = = 1. A special case is that I is 0, and I must not be in the set represented by J, which is meaningful. Let's skip the meaningless dp[i][j].

The for loop in the innermost layer is used to calculate the current value of DP [i] [J]. Using the idea of recursion, calculate the shortest path length starting from city I, passing through each city in the set represented by J only once, and then returning to city 0. We can take out each City in the set represented by J and try it once. Use K to traverse each city in J, that is, K from 1 to N-1 in the code, Then use an if to judge whether it is in J or not, and skip if it is not. For each city K in J, we calculate the shortest length from I to K, then from K to pass through all other cities only once, and then return to city 0. This shortest length can be expressed by dis[i][k] + DP [k] [J ^ (1 < < (k - 1))]. In this formula, the first half of dis[i][k] means to go from I to K first, The latter half represents the shortest path used to start from K, pass through other cities in J only once, and then return to city 0. We calculate all cities K in J, and the shortest one is the optimal choice starting from I, that is, the value of DP [i] [J]. Here, J ^ (1 < < (k - 1)) is to delete the city K from the set J, and the binary position corresponding to the city K in J can be 0. The value of J after deleting the city K must be smaller than that before deleting. Because we traverse j from small to large, the smaller position of J in DP [i] [J] must be calculated, and it can be used directly at this time, That's why dp[i][j] forms must be filled out column by column.

Finally, we determine the reverse path according to dp[i][j], and calculate dp[0][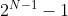]That is, the shortest path length. At this time, the known path can be expressed as? 0 The travel agent starts from city 0, visits all cities and then returns to city 0. We determine the path in reverse order. First, take the last returned City 0 as the successor city (suc), and find the penultimate City, that is, the one in front of the last 0? Which city in 1 - > n-1. The city is the calculation dp[0][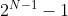]For the smallest city K, we recalculate dis [i] [k] + DP [k] [J ^ (1 < < (k - 1))], where I is the successor city (suc), i.e. City 0, and j is from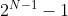Start. After confirming K, we'll confirm? k 0. At this time, set the found city K as the new suc, and delete K from the set represented by j. The reverse search knows that all locations are determined, which is the optimal path.

import numpy as np
from scipy.spatial import distance_matrix
import time

N = 20
train_graphs = np.genfromtxt('./data/tsp{}_train.txt'.format(N)).reshape(-1, N, 2)

for graph in train_graphs:
    total_st = dis_st = time.time()
    dis = distance_matrix(graph, graph)
    dis_ed = time.time()
    
    
    # DP
    dp_st = time.time()
    M = 1 << (N - 1) # Each binary bit of j represents whether the city of the number exists or not,
                     # The maximum of set j is. Except for city 0, cities 1 to N-1 are all in the set represented by j,
                     # At this time, the value of j is 2 ^ (n-1) ++ 2 ^ 1 = 2 ^ n - 1, i.e. 1 < < (n - 1) - 1
    
    # dp[i][j] represents the shortest distance from city I, passing through all cities in the set represented by j only once, and then returning to city 0
    dp = np.ones((N, M)) * np.inf  
    dp[:,0] = dis[:,0]  # dp[i][0] is the shortest distance from city I, through the empty set, and then back to city 0, that is, the length of edge I - > 0
    
    
    for j in range(1, M):  # Left closed right open, j traverses [1, M), i.e. [1, M - 1]
        for i in range(N):
            if i != 0 and (j >> (i - 1)) & 1 == 1:  # If the set of [i] [j] contains no meaning, DP means no city
                continue
            for k in range(1, N):
                if (j >> (k - 1)) & 1 != 1: # Traverse each city k in the set represented by j, and skip cities not in j
                    continue
                if dp[i][j] > dis[i][k] + dp[k][j ^ (1 << (k - 1))]: #Start from i to city k, and then to all cities except k in j
                    dp[i][j] = dis[i][k] + dp[k][j ^ (1 << (k - 1))]      
    dp_ed = time.time()                
    
    
    # Reverse order output path
    tour_st = time.time()
    suc = 0  # The next city number of the current city in the calculation dp[0][M-1]
    j = M - 1 # The set represented by j starts from the set containing all cities except City 0, and gradually deletes the city until the empty set
    tour = [0]
    for i in range(N - 1): # Except for city 0, other cities need to compare the length, and a total of N - 1 times is required
        min_len = np.inf
        for k in range(1, N):
            if (j >> (k - 1)) & 1 != 1: # Traverse all cities in the set represented by j, and skip those not in the set
                continue
            if min_len > dis[suc][k] + dp[k][j ^ (1 << (k - 1))]: # Find the k that minimizes dp[suc][j], that is, the city you are currently looking for
                min_len = dis[suc][k] + dp[k][j ^ (1 << (k - 1))]
                tmp = k
        suc = tmp
        tour.append(suc)
        j = j ^ (1 << (suc - 1))
    total_ed = tour_ed = time.time()
    
    
    print("tour: {} tour len: {}".format(tour, dp[0][M - 1]))
    print("Total duration: {}s \nDistances duration: {}s \nDP duration: {}s \nTour duration: {}s \n" \
          .format(total_ed - total_st, dis_ed - dis_st, dp_ed - dp_st, tour_ed - tour_st))
    #break

Give a set of test samples, which are randomly generated coordinates, and then use Gurobi to find the optimal solution

0.976064721802 0.245184117574 0.838277998552 0.949267213072 0.0676232302886 0.86665492153 0.954081065089 0.0962588315714 0.634296398269 0.404612925754 0.317284691223 0.540314315697 0.925689168873 0.0987753221956 0.761323280947 0.246835271084 0.374806546136 0.0575070527685 0.617327136243 0.678832372194 0.597783701296 0.489010648008 0.032855462271 0.883801127308 0.268434390934 0.675948261943 0.58618911836 0.755495660388 0.0376380290029 0.596520826603 0.834560198828 0.207960071941 0.879295374647 0.384123896197 0.300851987203 0.384237016803 0.643051333936 0.322582832126 0.000905072843543 0.685928559335 

0 3 6 15 7 8 17 5 14 19 11 2 12 13 1 9 10 4 18 16

Reference

Traveling salesman problem (dynamic programming method, super detailed)_ Benevolent Leshan, wise leshui blog - CSDN blog_ The travel agent asked kais