Some content sources: bestsort blog

Recommended blog:
CSDN: Nangong Yichen - thoroughly understand the two-dimensional tree array
CSDN: Lv1_kangdi - 2D tree array summary and template

The one-dimensional tree array sum[x] records the prefix and length of lowbit(x) from 1 to X

The two-dimensional tree array sum [x] [y] records the sum of areas from [1,1] to [x,y], with the height of lowbit(y) and the length of lowbit(x)

Example: Tree array - related template questions

One dimensional tree array

Illustration:

• Binary representation

lowbit() function

lowbit(x) represents the value corresponding to the lowest 1 in the binary expression of X

int lowbit(int x){
    return x & (-x);
}

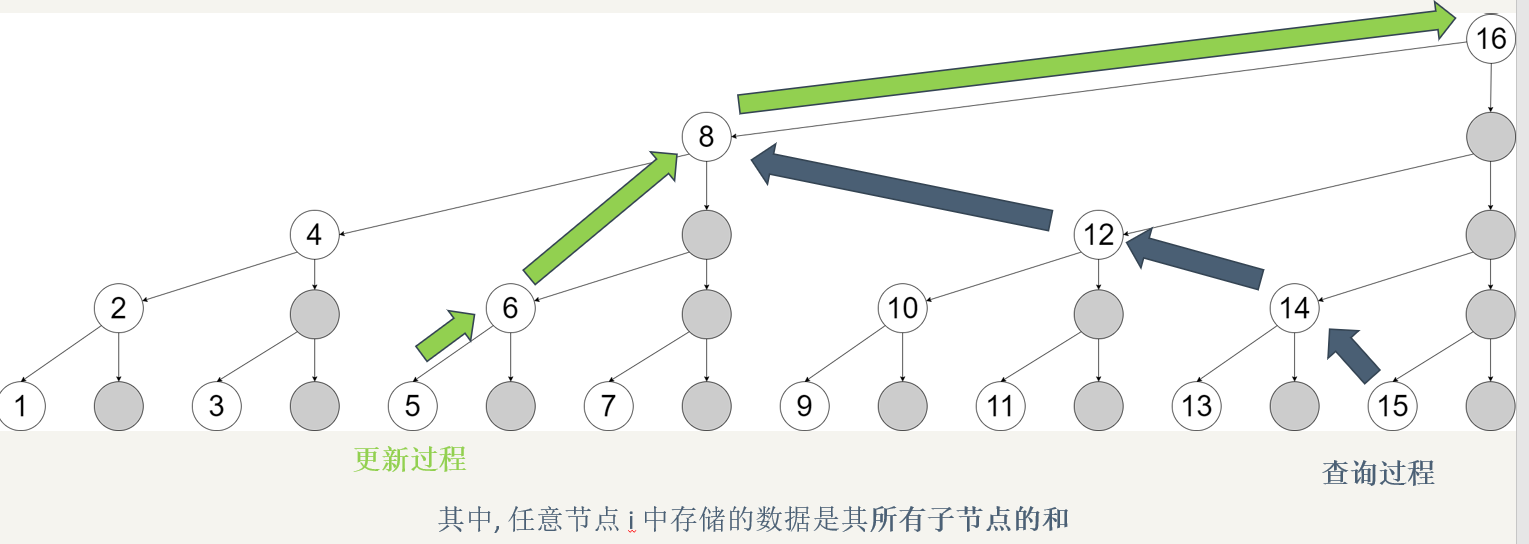
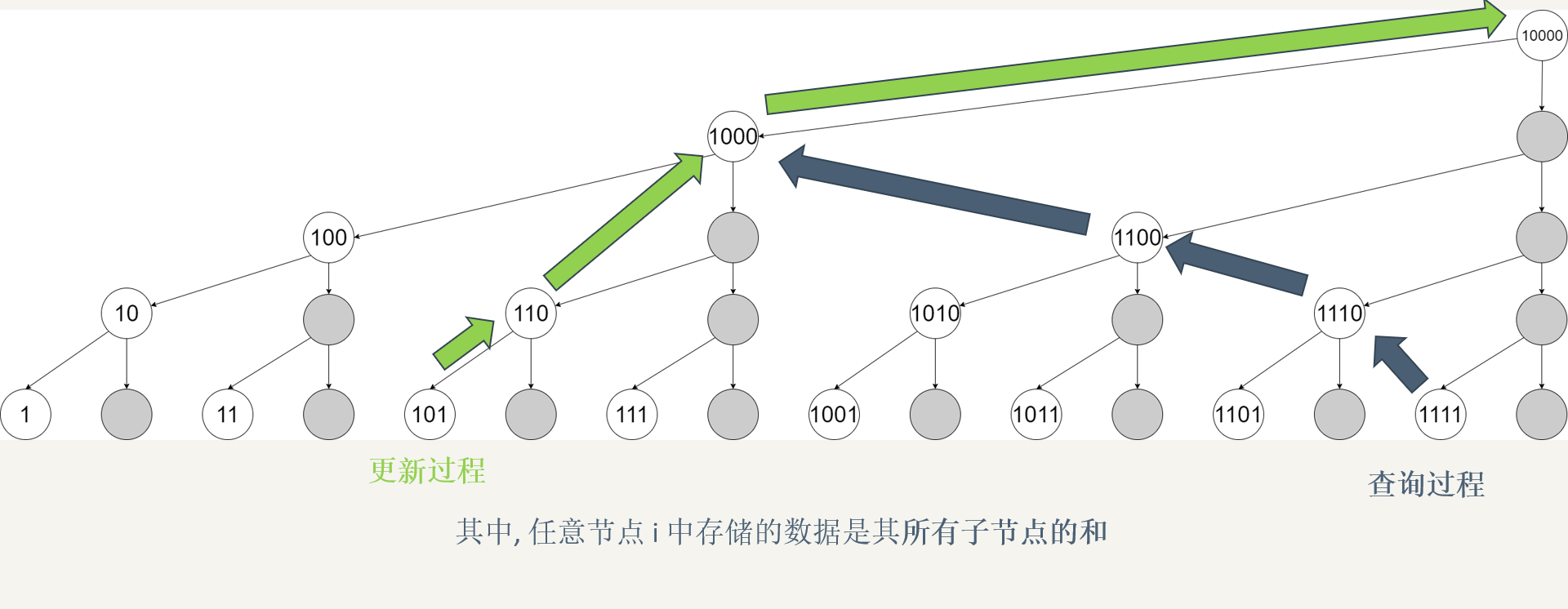
Single point modification

• Update from bottom to top to update the interval containing the point
• For example, when updating [5], the update order is sum [5], sum [6], sum [8], sum [16] (n < = 16)
• Binary representation is sum[101], sum[110], sum[1000], sum[10000]
• The upward update point is the current number + the value of the binary lowest 1 of the number (x + lowbit(x))

void updata(int id,int x,int n){
    while(id <= n){
        sum[id] += x;
        id += lowbit(id);
    }    
}

Interval query

• Query interval prefix and from bottom to top
• When querying, it is the sum of the current query number interval + the previous interval
• For example, when querying [1,13] intervals, the query intervals are sum[13], sum[12], sum[8] (sum[13] is the sum of [13,13], sum[12] is the sum of [9,12], and sum[8] is the sum of [1,8])
• Expressed in binary: sum[1101] + sum[1100] + sum[1000]
• The point queried upward is the current number - the value of the lowest binary 1 of the number (x - lowbit(x))
• The array sum[x] records the interval prefix sum of (x-lowbit (x), x)] (note that it is opened before closed)

int query(int id){
    int res = 0 ;
    while(id){
        res += sum[id];
        id -= lowbit(id);
    }
    return res;
}

Interval modification + single point query

Difference: a[i] is the original array, and the b[i] array is constructed so that b[i] = a[i] - a[i-1], that is, a[i] = a[i-1] + b[i] -- > a[i] is the prefix and sum of b[i]

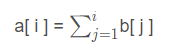
Interval modification:
The interval modification of a[i] is transformed into a single point modification of b[i] by difference: a [l, R] + X -- > b [l] + X, B [R + 1] - X

Single point query:
It is also an interval query that uses difference to convert it into b[i]: a [i] -- > b [1, R]

int a[N],b[N]; // a [] original array, b [] differential array

int lowbit(int id){
    return id & -id;
}

//Single point query
int query(int id){
    int res = 0;
    while(id) res += id, id -= lowbit(id);
    return res;
}

// Single point modification of differential array
void alter(int id,int x,int n){
    while(id <= n)  b[id] += x, id += lowbit(id);
}

//Interval modification
int update(int l,int r,int x,int n) {
    alter(l,x,n),alter(r+1,-x,n);
}

Interval modification + interval query

Similarly, use difference to build two arrays (explain the reasons below):
sum1[i] = b[i]
sum2[i] = b[i] * i

The principle of interval modification is basically the same as above: a [l, R] X -- > sum1 [l] + X, sum2 [R + 1] - X

Interval query: Sum_ a[l,r] --> (p+1) * sum1[i] - sum2[i] - ( (p+1) * sum1 - sum2[i] )

a[i] is the prefix sum of b[i], and the prefix sum of a[i] is the double prefix sum of b[i], as shown in the figure:

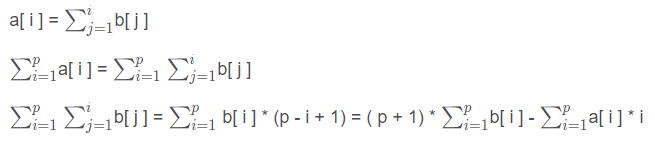
a[i] = b[i] + b[i-1] + b[i-2] +... + b[1]

a[1] = b[1]
a[2] = b[1] + b[2]
a[3] = b[1] + b[2] + b[3]
a[4] = b[1] + b[2] + b[3] +b[4]

In the prefix sum of a[p], b[1] uses p times, b[2] uses p-1 times, and so on (equation 3 above):

sum_a[p] = p * b[1] + (p-1) * b[2] + (p-3) * b[3] + ...+2 * b[p-1]+ 1 * b[p]

sum_a[p] = (p-i+1) * b[i] = (p+1) * b[i] - i * b[i]

Therefore, two formulas are used to maintain interval queries:
sum1[i] = b[i]
sum2[i] = b[i] * i

Note: when maintaining sum2 array, sum2[i] += id*x

int sum1[N], sum2[N];

//Point modification in interval modification
void alter(int id, int x, int n){
    int i = id;
    while(i <= n) sum1[i] += x, sum2[i] += id*x , i += lowbit(i);
}

// Interval modification
void update(int l,int r, int x, int n){
    alter(l, x, n), alter(r+1, -x, n);
}

// Point query in interval query
int query(int id){
    int res = 0, i = id;
    while(i){
        res += (id+1) * sum1[i] - sum2[i], i -= lowbit(i);
    }
    return res;
}

// Interval query
int range_query(int l,int r){
    return query(l) - query(r-1);
}

Two dimensional tree array

Recommended blog: 2D tree array summary and template:

Interval query + single point modification

int s[N][N], n ;

int lowbit(int x){
    return x & -x;
}

// Single point modification
void updata(int x, int y, int d){

    while(x <= n){
        int yy = y;
        while(yy <= n)
            s[x][yy] += d, yy += lowbit(yy);
        x += lowbit(x);
    }
}

// Interval query
int query(int x, int y){
    int res = 0;
    while(x){
        int yy = y;
        while(yy) res += s[x][yy], yy -= lowbit(yy);
        x -= lowbit(x);
    }
}

Interval modification + single point query

/**two-dimensional
 * Interval modification + single point query
 * **/

int a[N][N], b[N][N];

void updata(int x,int y, int d){
    while(x <= n){
        int yy = y;
        while(yy <= n)
            b[x][yy] += d, yy += lowbit(yy);
        x += lowbit(x);
    }
}

// modify
void range_updata(int x1,int y1,int x2,int y2, int d){
    updata(x1, y1, d);
    updata(x1+1, y2, -d);
    updata(x2, y1+1, -d);
    updata(x2+1, y2+1, d);
}

// query
int query(int x, int y){
    int res = 0;
    while(x){
        int yy = y;
        while(yy) res += b[x][yy], yy -= lowbit(yy);
        x -= lowbit(x);
    }
}

Interval modification + interval query

On the two-dimensional prefix and sum of points (x,y)

∑ i = 1 x ∑ j = 1 y ∑ k = 1 i ∑ h = 1 j d [ h ] [ k ] \sum_{i=1}^{x}\sum_{j=1}^{y}\sum_{k=1}^{i}\sum_{h=1}^{j}d[h][k] i=1∑x​j=1∑y​k=1∑i​h=1∑j​d[h][k]

∑ i = 1 x ∑ j = 1 y d [ i ] [ j ] ∗ ( x + 1 − i ) ∗ ( y + 1 − j ) \sum_{i=1}^{x}\sum_{j=1}^{y}d[i][j] * (x+1-i) * (y+1-j) i=1∑x​j=1∑y​d[i][j]∗(x+1−i)∗(y+1−j)

( x + 1 ) ∗ ( y + 1 ) ∗ ∑ i = 1 x ∑ j = 1 y d [ i ] [ j ] − ( y + 1 ) ∗ ∑ i = 1 x ∑ j = 1 y d [ i ] [ j ] ∗ i − ( x + 1 ) ∗ ∑ i = 1 x ∑ j = 1 y d [ i ] [ j ] ∗ j + ∑ i = 1 x ∑ j = 1 y d [ i ] [ j ] ∗ i ∗ j (x+1)*(y+1)*\sum_{i=1}^{x}\sum_{j=1}^{y}d[i][j]-(y+1)*\sum_{i=1}^{x}\sum_{j=1}^{y}d[i][j]*i-(x+1)*\sum_{i=1}^{x}\sum_{j=1}^{y}d[i][j]*j+\sum_{i=1}^{x}\sum_{j=1}^{y}d[i][j]*i*j (x+1)∗(y+1)∗i=1∑x​j=1∑y​d[i][j]−(y+1)∗i=1∑x​j=1∑y​d[i][j]∗i−(x+1)∗i=1∑x​j=1∑y​d[i][j]∗j+i=1∑x​j=1∑y​d[i][j]∗i∗j

Four arrays are maintained:
t1[i] [i] = d[i] [j]
t2[i] [j] = d[i] [j] * i
t3[i] [j] = d[i] [j] * j
t4[i] [j] = d[i] [j] * i * j

int t1[N][N], t2[N][N], t3[N][N], t4[N][N];

void updata(int x, int y, int d){
    while(x <= n){
        int yy = y;
        while(yy <= n){
            t1[x][yy] += d;
            t2[x][yy] += d*x;
            t3[x][yy] += d*y;
            t4[x][yy] += d*x*y;
            yy += lowbit(yy);
        }
        x += lowbit(x);
    }
}

//Interval modification
void range_updata(int x1,int y1,int x2,int y2,int d){
    updata(x1, y1, d);
    updata(x1 + 1, y2, -d);
    updata(x2, y1 + 1, -d);
    updata(x2 + 1, y2 + 1, d);
}

int query(int x, int y){
    int res = 0;
    while(x){
        int yy = y;
        while(yy){
            res += t1[x][yy]*(x+1)*(y+1) - t2[x][yy]*(y+1) - t3[x][yy]*(x+1) + t4[x][yy];
            yy -= lowbit(yy);
        }
        x-=lowbit(x);
    }
}

//Interval query
int range_query(int x1,int y1,int x2,int y2){
    return query(x2,y2) - query(x1-1,y2) - query(x2,y1-1) + query(x1-1,y1-1);
}