What I want to share with you today is a tree array. What is a tree array? According to the name, we can roughly deduce that we use our common array to simulate the tree structure. So what problems can he solve? I'll explain it at the end.
First, let's talk about what the tree leader looks like?
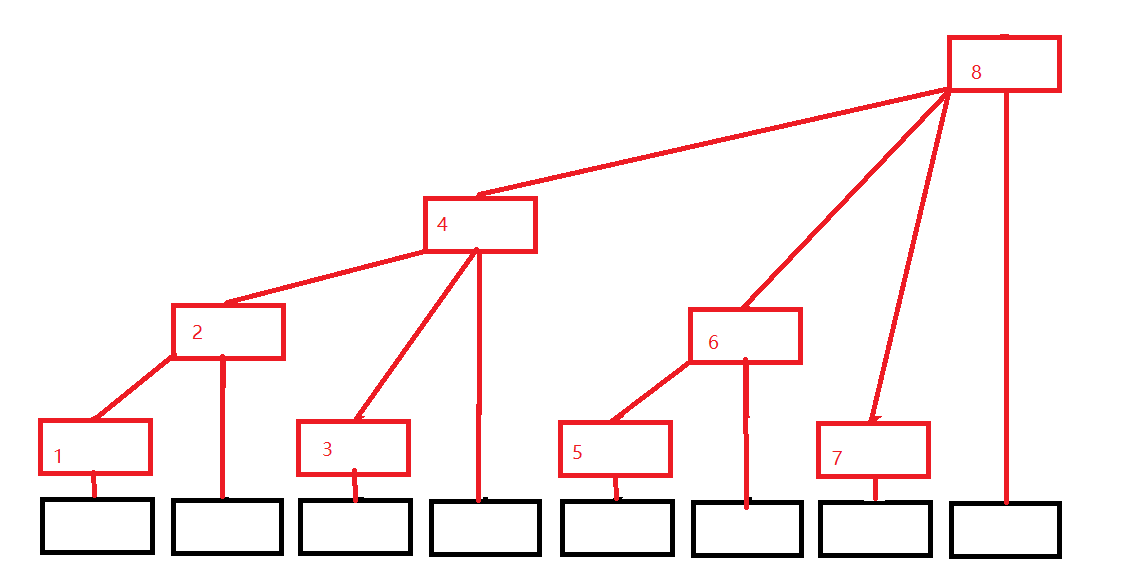
In this picture, we can see an array with two elements. The black array represents the original array, let's use a [] to represent it, and the red array represents the tree array we want to construct, let's use b []. Each red color array stores the sum of the node elements below it. It is not difficult to see from the picture:
c[1]=a[1]
c[2]=c[1]+a[2]=a[1]+a[2]
c[3]=a[3]
c[4]=c[2]+c[3]+a[4]=a[1]+a[2]+a[3]+a[4]
c[5]=a[5]
c[6]=c[5]+a[6]=a[5]+a[6]
c[7]=a[7]
c[8]=c[4]+c[6]+c[7]+a[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]
Now let's find the law from some of the above examples; It is not difficult to find that if n is a power of 2, then C [n] = a [1] + a [2] ++ A [n], so what is the law of such n in binary representation? We find that in its binary representation, only the highest bit is 1, and the other bits are 0. Does this have anything to do with the lowest to highest bit of the number under the binary representation? In fact, C [n] = a [n-2 ^ m + 1] + a [n-2 ^ m + 2] ++ A [n] where m is the length of 0 in the binary representation of N, starting from the low bit until the first 1 is found.
So how to find this m, M = n & (- n); For example:
If n is 12, the binary representation is 1100, then its inverse code is the inverse of each bit, i.e. 0011, then all the places that are 1 at this time are 0 in N, then adding its inverse code to 1 will keep the first 1 and its previous numbers in the original n unchanged, and the subsequent numbers will be reversed, so they will keep the first number that is 1 in their & operation, which is the principle of lowbit function.
Our common interval problems mainly include the following:
(1) Single point update, single point query;
(2) Single point update, interval query;
(3) Interval update, single point query;
(4) Interval update, interval query;
The first problem can be realized with an ordinary one-dimensional array. I won't say much here. I mainly want to introduce the processing methods of the last three problems.
Let's deal with the second problem first. If we modify a[i], the array we construct stores the sum of array a, so it will certainly be affected, but which elements are affected? In fact, it is c[i+lowbit(i)],c[i+lowbit(i)+lowbit(i+lowbit(i))]; It is not difficult to find that this operation can be solved by lowbit function. The board for creating a tree array is given below:
int lowbit(int x)//Find the position where the first one in x is 1
{
return x&(-x);
}
void update(int x,int k)//Construct a tree array
{
while(x<=n)
{
c[x]+=k;
x+=lowbit(x);
}
}
int sum(int i)//Implement query
{
int res=0;
while(i>0)
{
res+=c[i];
i-=lowbit(i);
}
return res;
}This is the board of single point update and interval query. Here is an example: (pure template) Luogu 3374
Title Description
For example, given a sequence of numbers, you need to perform the following two operations:
-
Add a number to x
-
Find the sum of each number in an interval
Input format
The first row contains two positive integers, n,m, which respectively represent the number of numbers in the sequence and the total number of operations.
The second line contains n ¢ integers separated by spaces, where the ¢ i ¢ number represents the initial value of the ¢ i ¢ item of the sequence.
Next, each line of # m # contains # 3 integers, representing an operation, as follows:
-
1 x k , meaning: add the , x , number to , K
-
2 x,y meaning: the sum of each number in the output interval [x,y]
Input and output samples
Input
5 5 1 5 4 2 3 1 1 3 2 2 5 1 3 -1 1 4 2 2 1 4
Output
14 16
#include<iostream>
using namespace std;
int a[500010],c[500010];
int n,m;
int lowbit(int x)
{
return x&(-x);
}
void update(int x,int k)
{
while(x<=n)
{
c[x]+=k;
x+=lowbit(x);
}
}
int sum(int i)
{
int res=0;
while(i>0)
{
res+=c[i];
i-=lowbit(i);
}
return res;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
update(i,a[i]);//The constructed array is updated every time a value is entered
}
int a,b,c;
while(m--)
{
cin>>a>>b>>c;
if(a==1)
update(b,c);
if(a==2)
cout<<(sum(c)-sum(b-1))<<endl;
}
return 0;
}Now let's consider the third problem, that is, single point interval update and single point query; The violent method is to modify the numbers in the modification interval one by one, but this complexity is obviously a little high. How can we achieve this operation through a tree array? Let's think about the interval update and single point query of ordinary arrays. We constructed a difference array at that time. Similarly, we can also construct a difference group D [], so d [n] means a[n]-a[n-1], so C [n] = D [1] + D [2] + D [3] ++ d[n]=a[1]+(a[2]-a[1])+(a[3]-a[2])+....+ (a[n]-a[n-1]) = a [n], that is, the result of our single point query is the prefix sum of Array D, that is, the value of the corresponding array a. Here is an example: (pure template)
For example, given a sequence of numbers, you need to perform the following two operations:
-
Add {x to each number in a certain interval;
-
Find the value of a number.
Input format
The first row contains two integers N and M, which respectively represent the number of numbers in the sequence and the total number of operations.
The second line contains N ¢ integers separated by spaces, where the ¢ i ¢ number represents the initial value of the ¢ i ¢ item of the sequence.
Next, each line of ^ M ^ contains ^ 2 ^ or ^ 4 integers, representing an operation, as follows:
Operation # 1: Format: 1 x y k # meaning: add # kk to each number in the interval [x,y];
Operation # 2: Format: 2 x # meaning: output the value of the # x # number.
Output format
The output contains several lines of integers, which is the result of all operations {2}.
Input and output samples
Input
5 5 1 5 4 2 3 1 2 4 2 2 3 1 1 5 -1 1 3 5 7 2 4
Output
6 10
Here is the code
#include<iostream>
using namespace std;
int a[500010],c[500010];
int n,m;
int lowbit(int x)
{
return x&(-x);
}
void update(int x,int k)
{
while(x<=n)
{
c[x]+=k;
x+=lowbit(x);
}
}
int sum(int i)
{
int res=0;
while(i>0)
{
res+=c[i];
i-=lowbit(i);
}
return res;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
update(i,a[i]-a[i-1]);//What we construct is a differential array
}
int a,b,c,d;
while(m--)
{
cin>>a;
if(a==1)
{
cin>>b>>c>>d;
update(b,d);//Update array left boundary
update(c+1,-d);//Update array right boundary
} if(a==2) { cin>>c; cout<<sum(c)<<endl; } } return 0; }The last problem is interval update interval query. How should we construct a tree array? Well, we still use the idea of difference. I can't type some symbols yet. I'll write the analysis process on paper. Ha ha, the following pictures are attached:

#include<iostream>
using namespace std;
int a[500010],c[500010],d[500010];
int n,m;
int lowbit(int x)
{
return x&(-x);
}
void update(int x,int k)
{
int t=x-1;
while(x<=n)
{
c[x]+=k;//Maintain differential array
d[x]+=t*k;//Maintenance (i-1) * d[i]
x+=lowbit(x);
}
}
int sum(int i)//Sum
{
int res=0,x=i;
while(i>0)
{
res+=x*c[i]-d[i];
i-=lowbit(i);
}
return res;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
update(i,a[i]-a[i-1]);
}
int a,b,c,d;
while(m--)
{
cin>>a;
if(a==1)//Add d to the interval b~c
{
cin>>b>>c>>d;
update(b,d);
update(c+1,-d);
}
if(a==2)//Sum of output b~c intervals
{
cin>>b>>c;
cout<<sum(c)-sum(b-1)<<endl;
}
}
return 0;
}Summary: the functionality of tree array is not as strong as line segment tree, but its code is relatively simple and can be used to solve many basic problems on interval.
After coding for nearly three hours, the code is finally finished. The code is not easy. If you can help everyone, I hope you can do something and give a praise before you go. Thank you~