tree
What is a tree?
Tree is a kind of data structure similar to the linked list, but the nodes of the linked list simply point to their successor nodes in a linear way, and one node of the tree can point to many nodes; number is a typical nonlinear structure; tree structure is a method to express the hierarchical graph structure;
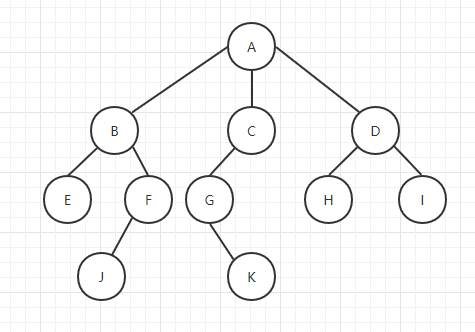
Related terms
- Root node: the root node is A node without parents. There is at most one root node in A tree (as shown in the above figure, node A is the root node).
- Edge: the edge represents the link from the parent node to the child node (as shown in the above figure);
- Leaf node: nodes without child nodes are called leaf nodes (such as E, J, K, H and I)
- Brother node: all child nodes with the same parent node are called brother nodes (B, C, D are brother nodes of A, E, F are brother nodes of B);
- Ancestor node: if there is A path from root node to node Q, and node p appears in this path, then node p can be called the ancestor node of node Q, and node q is also called the descendant node of p (for example, A, C and G are the ancestor nodes of K).
- Node size: node size refers to the number of descendants, including itself. (the size of subtree C is 3);
- Tree layer: the set of all nodes at the same depth is called the tree layer (B, C and D have the same layer, and the structure in the above figure has four layers of 0 / 1 / 2 / 3);
- Node depth: refers to the path length from the root node to the node (the depth of G point is 2, A-C-g);
- Node height: refers to the path length from the node to the deepest node. Tree height refers to the path length from the root node to the deepest node in the book. The height of the tree containing only the root node is 0. (the height of B is 2, b-F-J);
- Tree height: the maximum height of all nodes in the tree, and the depth of the tree is the maximum depth of all nodes in the tree. For the same tree, its depth and height are the same, but for each node, its depth and height are not necessarily the same;
Two fork tree
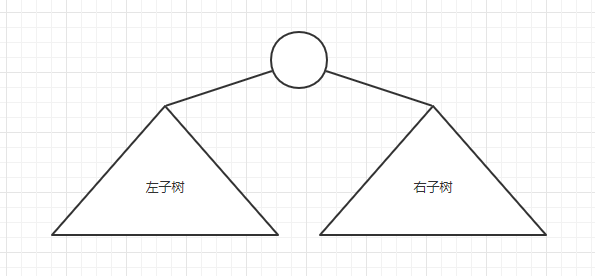
If each node in a tree has 0, 1 or 2 child nodes, then the tree is called a binary tree; an empty tree is also an effective binary tree, and a binary tree can be seen as consisting of a root node and two disjoint subtrees (called left subtree and right subtree respectively), as shown in the following figure.
Types of binary trees
Strict binary tree: each node in a binary tree has either two child nodes or no child nodes
Full binary tree: each node in a binary tree has exactly two child nodes and all leaf nodes are in the same layer
Complete binary tree: before defining a complete binary tree, the height of the binary tree is assumed to be h; for a complete binary tree, if all nodes are numbered successively from left to right, from top to bottom (assuming the number of the root node is 1), then the complete sequence from 1 to n (n is the total number of nodes) is obtained rigidly, and the null pointer is also assigned with a number during the traversal process, if all nodes are numbered successively from left to right, from top to bottom. If the depth of the node is h or h-1, and there is no missing number in the node number sequence, then such a binary tree is called a complete binary tree.
(just make sure that all nodes before the last node are complete)
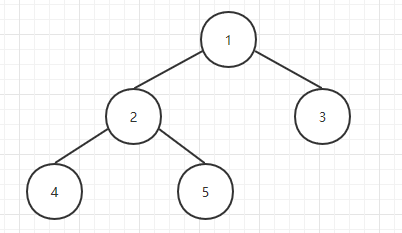
Application of binary tree
- Expression tree in compiler;
- Huffman coding tree for data compression algorithm;
- It supports searching, inserting and deleting in the set, and its average time complexity is O(lognn) binary search tree (BST).
- Priority queue (PQ), which supports the search and deletion of the smallest (or largest) data elements in the set in logarithmic time (worst case);
Traversal of binary tree
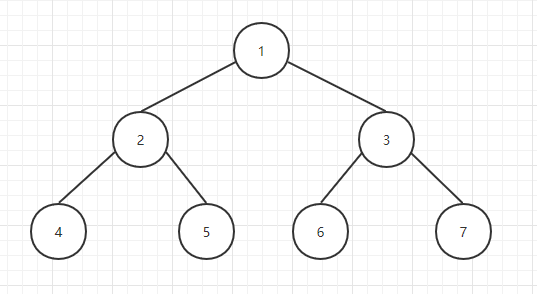
The process of accessing all nodes in the tree is called tree traversal. In the process of traversal, each node can only be processed once, although it may be accessed many times; according to the different processing order of nodes. Different traversal methods can be defined, and the traversal classification can be divided according to the order in which the current node is processed:
Preorder traversal
In the pre order traversal, each node is processed before its subtree traversal, which is the most easy to understand convenient method. However, although each node has been processed before its subtree, some information still needs to be kept in the process of moving down. For example, in the above figure, first visit node 1, then traverse its left subtree, and finally traverse its right subtree, so when left After traversing the subtree, you must return to its right subtree to continue traversing; in order to move to the right subtree after traversing the left subtree, you must keep the information of the root node, and the abstract data type that can realize the information storage is obviously the stack, because it is the structure of LIFO, so it can collect the information in reverse order and return to the right subtree; (first visit the root node , then access the left node, and finally access the right node (root - > left - > right))
The preamble traversal can be defined as follows:
- Access the root node;
- Traversing the left subtree in the way of pre order traversal;
- Traversing the right subtree in the way of pre order traversal;
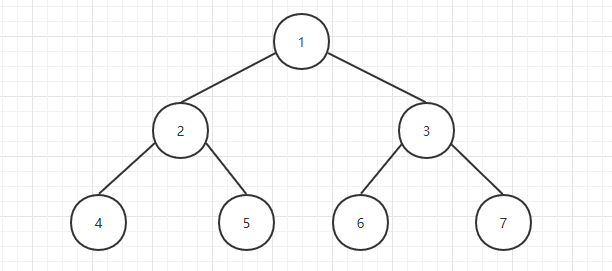
The output sequence of the tree shown in the figure above is: 1 24 5 3 6 7
void preOrder(BinaryTreeNode root) {
if (null != root) {
System.out.println(root.getData());
preOrder(root.getLeft());
preOrder(root.getRight());
}
}Sequential traversal
Access the left node first, then the root node, and finally the right node (left - > root - > right)
Based on the middle order traversal, the output order of the middle order traversal of the tree shown above is: 4 25 1 6 3 7
void inOrder(BinaryTreeNode root) {
if (null != root) {
inOrder(root.getLeft());
System.out.println(root.getData());
inOrder(root.getRight());
}
}Post order traversal
Access the left node first, then the right node, and finally the root node (left - > right - > root)
For the binary tree shown in the figure above, the output sequence generated by subsequent traversal is: 4 5 2 6 7 3 1
void postOrder(BinaryTreeNode root) {
if (null != root) {
postOrder(root.getLeft());
postOrder(root.getRight());
System.out.println(root.getData());
}
}level traversal
- Access the root node;
- When accessing layer l, the nodes of layer l+1 are saved in the queue in order.
- Enter the next layer and access all nodes of the layer;
- Repeat the above operations until all layers are accessed;
For the binary tree shown in the figure above, the output sequence generated by level traversal is: 1 23 4 5 6 7
void levelOrder(BinaryTreeNode root) {
BinaryTreeNode temp;
LoopQueue Q = new LoopQueue();
if (null == root) {
return;
}
Q.enqueue(root);
while (!Q.isEmpty()) {
temp = Q.dequeue();
// Process current node
System.out.println(temp.getData());
if (temp.getLeft()) {
Q.enqueue(temp.getLeft());
}
if (temp.getRight()) {
Q.enqueue(temp.getRight());
}
}
// Delete all data in the queue
Q.deletequeue();
}
Binary search tree
In the binary search tree, the elements of all the left sub tree nodes are smaller than the data of the root node, and the elements of all the right sub tree nodes are larger than the data of the root node. Note that every node in the tree should meet this property.
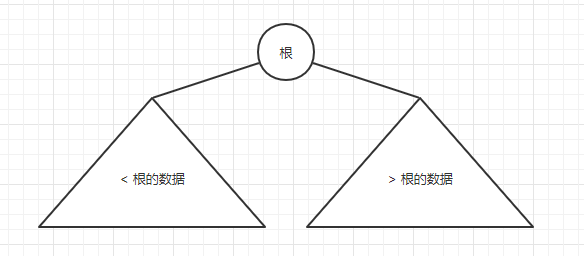
Implementation of binary search tree
Some commonly used methods are included, including several traversal methods, query, deletion, etc., for reference only:
public class BST<E extends Comparable<E>> {
private class Node{
public E e;
public Node left, right;
public Node(E e){
this.e = e;
left = null;
right = null;
}
}
private Node root;
private int size;
public BST(){
root = null;
size = 0;
}
public int size(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
// Add a new element e to the binary search tree
public void add(E e){
root = add(root, e);
}
// Insert element e into binary search tree with node as root, recursive algorithm
// Returns the root of the binary search tree after inserting a new node
private Node add(Node node, E e){
if(node == null){
size ++;
return new Node(e);
}
if(e.compareTo(node.e) < 0)
node.left = add(node.left, e);
else if(e.compareTo(node.e) > 0)
node.right = add(node.right, e);
return node;
}
// See if the binary search tree contains element e
public boolean contains(E e){
return contains(root, e);
}
// See if the binary search tree with node as root contains element e, recursive algorithm
private boolean contains(Node node, E e){
if(node == null)
return false;
if(e.compareTo(node.e) == 0)
return true;
else if(e.compareTo(node.e) < 0)
return contains(node.left, e);
else // e.compareTo(node.e) > 0
return contains(node.right, e);
}
// Preorder traversal of binary search tree
public void preOrder(){
preOrder(root);
}
// Pre order traversal of binary search tree with node as root, recursive algorithm
private void preOrder(Node node){
if(node == null)
return;
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
// Non recursive preorder traversal of binary search tree
public void preOrderNR(){
Stack<Node> stack = new Stack<>();
stack.push(root);
while(!stack.isEmpty()){
Node cur = stack.pop();
System.out.println(cur.e);
if(cur.right != null)
stack.push(cur.right);
if(cur.left != null)
stack.push(cur.left);
}
}
// Middle order traversal of binary search tree
public void inOrder(){
inOrder(root);
}
// Middle order traversal of binary search tree with node as root, recursive algorithm
private void inOrder(Node node){
if(node == null)
return;
inOrder(node.left);
System.out.println(node.e);
inOrder(node.right);
}
// Post order traversal of binary search tree
public void postOrder(){
postOrder(root);
}
// Post order traversal of binary search tree with node as root, recursive algorithm
private void postOrder(Node node){
if(node == null)
return;
postOrder(node.left);
postOrder(node.right);
System.out.println(node.e);
}
// Sequence traversal of binary search tree
public void levelOrder(){
Queue<Node> q = new LinkedList<>();
q.add(root);
while(!q.isEmpty()){
Node cur = q.remove();
System.out.println(cur.e);
if(cur.left != null)
q.add(cur.left);
if(cur.right != null)
q.add(cur.right);
}
}
// Finding the minimum elements of binary search tree
public E minimum(){
if(size == 0)
throw new IllegalArgumentException("BST is empty!");
return minimum(root).e;
}
// Returns the node of the minimum value of the binary search tree with node as the root
private Node minimum(Node node){
if(node.left == null)
return node;
return minimum(node.left);
}
// Find the largest element of binary search tree
public E maximum(){
if(size == 0)
throw new IllegalArgumentException("BST is empty");
return maximum(root).e;
}
// Returns the node where the maximum value of the binary search tree based on node is located
private Node maximum(Node node){
if(node.right == null)
return node;
return maximum(node.right);
}
// Delete the node of the minimum value from the binary search tree and return the minimum value
public E removeMin(){
E ret = minimum();
root = removeMin(root);
return ret;
}
// Delete the smallest node in the binary search tree with node as root
// Return to the root of the new binary search tree after deleting the node
private Node removeMin(Node node){
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// Remove the node with the maximum value from the binary search tree
public E removeMax(){
E ret = maximum();
root = removeMax(root);
return ret;
}
// Delete the largest node in the binary search tree with node as root
// Return to the root of the new binary search tree after deleting the node
private Node removeMax(Node node){
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
// Remove the node with element e from the binary search tree
public void remove(E e){
root = remove(root, e);
}
// Delete the node whose median value is e in the binary search tree whose root is node, recursive algorithm
// Return to the root of the new binary search tree after deleting the node
private Node remove(Node node, E e){
if( node == null )
return null;
if( e.compareTo(node.e) < 0 ){
node.left = remove(node.left , e);
return node;
}
else if(e.compareTo(node.e) > 0 ){
node.right = remove(node.right, e);
return node;
}
else{ // e.compareTo(node.e) == 0
// The left subtree of the node to be deleted is empty
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
// When the right subtree of the node to be deleted is empty
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
// When the left and right subtrees of the node to be deleted are not empty
// Find the smallest node larger than the node to be deleted, that is, the smallest node of the right subtree of the node to be deleted.
// Replace the location of the node to be deleted with this node
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
generateBSTString(root, 0, res);
return res.toString();
}
// Generate a string describing binary tree with node as root node and depth as depth
private void generateBSTString(Node node, int depth, StringBuilder res){
if(node == null){
res.append(generateDepthString(depth) + "null\n");
return;
}
res.append(generateDepthString(depth) + node.e +"\n");
generateBSTString(node.left, depth + 1, res);
generateBSTString(node.right, depth + 1, res);
}
private String generateDepthString(int depth){
StringBuilder res = new StringBuilder();
for(int i = 0 ; i < depth ; i ++)
res.append("--");
return res.toString();
}
}
public List<Integer> inorderTraversal(TreeNode root) {
List result = new ArrayList();
if (null != root) {
result.addAll(inorderTraversal(root.left));
result.add(root.val);
result.addAll(inorderTraversal(root.right));
}
return result;
}