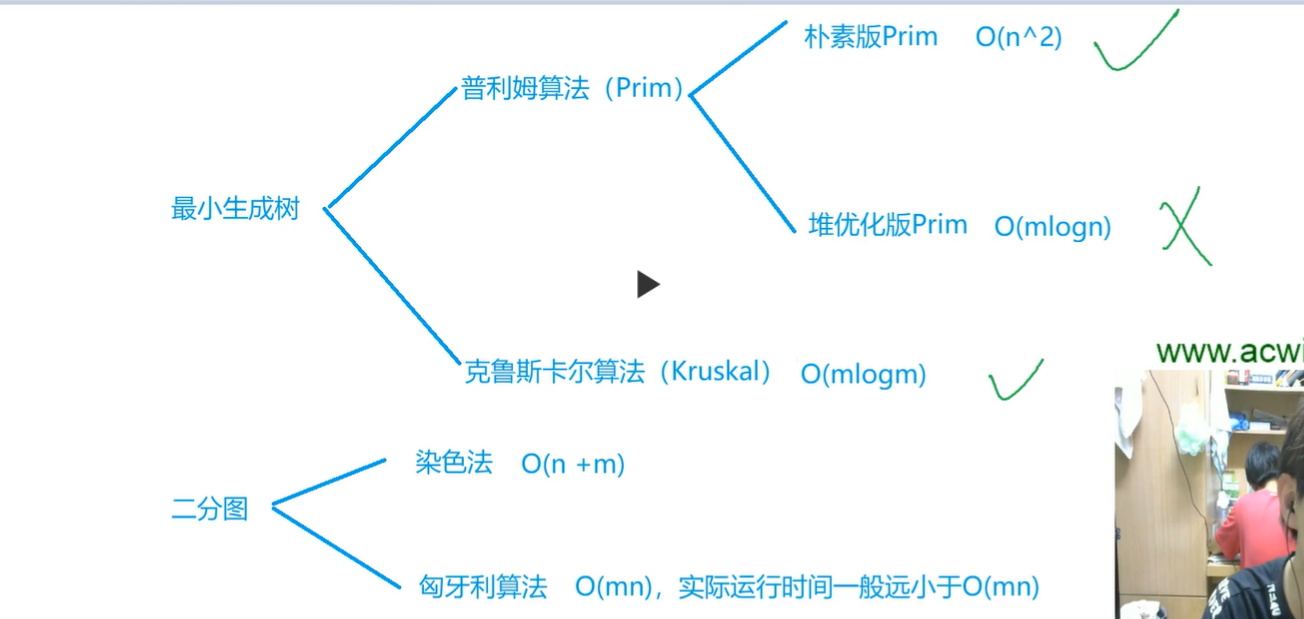
Minimum number of spanning trees - prim algorithm O(n^2):
Purpose: to find the dense graph of the minimum spanning tree
What prim algorithm does is: given an undirected graph, select several edges in the graph to connect all nodes of the graph. The minimum sum of side lengths is required. In graph theory, it is called finding the minimum spanning tree.
prim algorithm adopts a greedy strategy.
Each time the nearest point from the connected part and the edge corresponding to the point are added to the connected part, the connected part gradually expands, and finally the whole graph is connected, and the sum of edge lengths is the smallest.
Contact prim with dijkstra:
Dist in prim is used to store the shortest distance from each node to the spanning tree, and dist in dijkstra is used to store the shortest distance from each node to the source point
1 #include <iostream> 2 #include <cstring> 3 4 using namespace std; 5 6 const int N=510,INF=0x3f3f3f3f; 7 int res,n,m; 8 int dist[N]; //Store the shortest distance from each node to the spanning tree 9 int pre[N]; //Forward node of each node 10 int g[N][N]; 11 bool st[N]; //Judge whether the node is added to the spanning tree 12 13 void prime() 14 { 15 memset(dist,0x3f,sizeof dist); 16 for(int i=0;i<n;i++) 17 { 18 int t=-1; 19 for(int j=1;j<=n;j++)//The closest point in the connected block to a point in the connected block cannot be found 20 { 21 if(!st[j]&&(t==-1||dist[j]<dist[t]))t=j; 22 } 23 24 if(i&&dist[t]==INF) //If there is a point in the connected block, but it is found dist still inf 25 { //If there are unconnected points, there is no minimum spanning tree 26 res=INF; 27 break; 28 } 29 if(i)res+=dist[t]; //On the first cycle, dist[0]=inf 30 //At this time, the connected block has only one point and the distance is 0 31 st[t]=1; //explain t Points have been added to the spanning tree, but not necessarily at this time dist[t]minimum 32 33 for(int j=1;j<=n;j++) //use t Update the distance of other points (whether in connected block or not) 34 { 35 if(dist[j]>g[t][j]) 36 { 37 dist[j]=g[t][j]; 38 pre[j]=t; //from t reach j The distance is shorter, j The precursor to t 39 } 40 } 41 } 42 43 } 44 45 void path()//Output edges 46 { 47 for(int i=n;i>1;i--)printf("%d %d\n",i,pre[i]); 48 49 } 50 51 int main() 52 { 53 scanf("%d%d",&n,&m); 54 memset(g,0x3f,sizeof g); 55 while(m--) 56 { 57 int u,v,w; 58 scanf("%d%d%d",&u,&v,&w); 59 g[u][v]=g[v][u]=min(g[u][v],w); //Undirected graph 60 } 61 62 prime(); 63 path(); 64 65 if(res==INF)puts("impossible"); 66 else printf("%d\n",res); 67 68 69 70 return 0; 71 }
Minimum number of spanning trees - kruskal algorithm O(mlogm):
Purpose: sparse graph of minimum spanning tree
Method: 1 Put the edges and edge weights into the structure and sort them from small to large.
2. Initialize n points as the ancestor node of the union query set
3. For m edge loops, if two points are not in the same set, merge the set, sum the edge weights, and the number of edges++
4. If the number of edges is not equal to n-1, it means that the minimum spanning tree cannot be constructed. Otherwise, the edge weight sum is output
1 #include <iostream> 2 #include <algorithm> 3 using namespace std; 4 5 const int M=2e5+10; 6 int p[M],cnt,res; //cnt Represents the number of sides in the set, res Represents the sum of weights 7 int n,m; 8 struct EDGE 9 { 10 int a,b,w; 11 bool operator<(const EDGE &W)const 12 { 13 return w<W.w; 14 } 15 }edges[M]; 16 17 int find(int x) //And look up the set to find the ancestor node 18 { 19 if(p[x]!=x)p[x]=find(p[x]); 20 return p[x]; 21 } 22 23 void kruskal() 24 { 25 sort(edges,edges+m); //Each edge weight is sorted from small to large 26 for(int i=1;i<=n;i++)p[i]=i; //Joint query set ancestor node assignment 27 28 for(int i=0;i<m;i++) 29 { 30 int a=edges[i].a,b=edges[i].b, w=edges[i].w; 31 if(find(a)!=find(b)) //If a,b If the set is not the same, merge 32 { 33 p[find(b)]=find(a); 34 cnt++; 35 res+=w; 36 } 37 } 38 } 39 40 int main() 41 { 42 scanf("%d%d",&n,&m); 43 for(int i=0;i<m;i++) 44 { 45 int u,v,w; 46 scanf("%d%d%d",&u,&v,&w); 47 edges[i]={u,v,w}; 48 } 49 50 kruskal(); 51 if(cnt!=n-1)puts("impossible"); 52 //If there are not enough sides in the set n-1 Bar, indicating that all points are not connected and there is no minimum spanning tree 53 else printf("%d\n",res); 54 55 56 return 0; 57 }
Bipartite graph - coloring method O(m+n):
Bipartite diagram:
Dividing all points into two sets so that all edges only appear between sets is a bipartite graph
Bipartite graph: it must not contain odd rings, but may contain rings with even length, not necessarily connected graphs
Idea dfs:
Dyeing can use 1 and 2 to distinguish different colors, and 0 indicates no dyeing
Traverse all points, and dfs the non stained points each time. The default color is 1 or 2
Because a successful coloring of a point does not mean that the whole graph is a bipartite graph, only a failed coloring of a point can immediately break/return
Dyeing failure is equivalent to the existence of two adjacent dots dyed with the same color
1 #include <iostream> 2 #include <cstring> 3 using namespace std; 4 5 const int N=2e5+10; 6 int n,m; 7 int h[N],ne[N],e[N],idx; 8 int color[N]; //0 Means no color, 1 means red, 2 means blue 9 10 void add(int a,int b) 11 { 12 e[idx]=b;ne[idx]=h[a];h[a]=idx++; 13 } 14 15 bool dfs(int t,int p) 16 { 17 color[t]=p; //take t Dot coating p 18 for(int i=h[t];i!=-1;i=ne[i]) //At and t Search in connected points 19 { 20 int j=e[i]; 21 if(!color[j]) //If j The dots are not painted 22 { 23 if(dfs(j,3-color[t])==0)return 0; 24 //When j Coating and t If there is a duplicate color in the opposite color, it will fail 25 } 26 else if(color[j]==color[t])return 0; 27 //If j Coloring and t Same, repeat color, failure 28 } 29 return 1; 30 } 31 32 int main() 33 { 34 scanf("%d%d",&n,&m); 35 memset(h,-1,sizeof h); 36 for(int i=1;i<=m;i++) 37 { 38 int u,v; 39 scanf("%d%d",&u,&v); 40 add(u,v);add(v,u); //Undirected graph 41 } 42 43 bool flag=1; 44 for(int i=1;i<=n;i++) 45 { 46 if(!color[i]&&!dfs(i,1)) //If i There is no coloring, and there is coloring contradiction after the search 47 { //Failed 48 flag=0; 49 break; 50 } 51 52 } 53 54 if(flag)puts("Yes"); 55 else puts("No"); 56 57 58 59 return 0; 60 }
Bipartite graph - Hungarian algorithm O(m*n):
Purpose: find the maximum matching number of bipartite graph
#include <iostream> #include <cstring> using namespace std; const int M=1e5+10,N=510; int h[N],ne[M],e[M],idx; int n1,n2,m,res; bool st[N]; int match[N]; void add(int a,int b) //Male to female, no need for female to male { ne[idx]=h[a];e[idx]=b;h[a]=idx++; } bool find(int u) { for(int i=h[u];i!=-1;i=ne[i]) //Go through all the girls you like { int j=e[i]; if(!st[j]) //If this girl hasn't been booked in this round { st[j]=1; //The boy made an appointment if(!match[j]||find(match[j])) { //If a girl doesn't have a boyfriend or her boyfriend can find a girlfriend from the girls she likes match[j]=u; //This girl is with u Together return 1; //Match successful } } } return 0; } int main() { scanf("%d%d%d",&n1,&n2,&m); memset(h,-1,sizeof h); for(int i=1;i<=m;i++) { int u,v; scanf("%d%d",&u,&v); add(u,v); } for(int i=1;i<=n1;i++) { memset(st,-1,sizeof st); //Every boy tries the girl he likes (whether he has a boyfriend or not) if(find(i))res++; } printf("%d\n",res); return 0; }