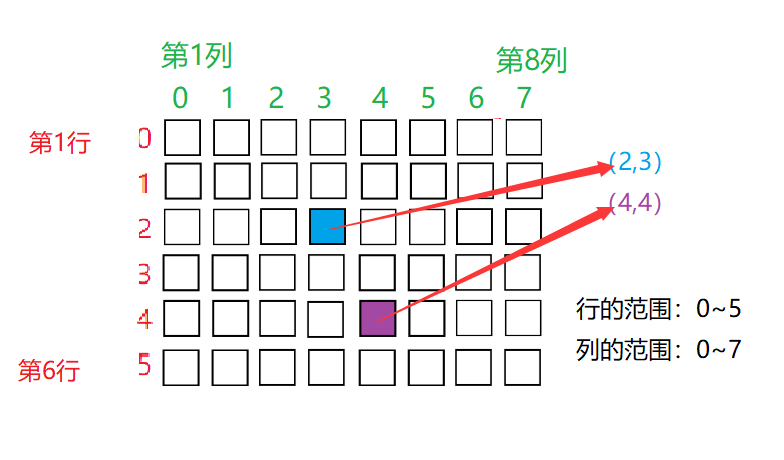
The so-called two-dimensional array is just a table composed of rows and columns, Matrix. When we access the elements in this Matrix, we determine them according to the row and column subscripts of the elements.
How is the two-dimensional array stored in memory?
Whether it's a two-dimensional array or a multi-dimensional array, they are a one-dimensional array
Especially for a two-dimensional array, it is nothing more than a one-dimensional array, but each element in the one-dimensional array is another one-dimensional array!
Use the diagram to explain:
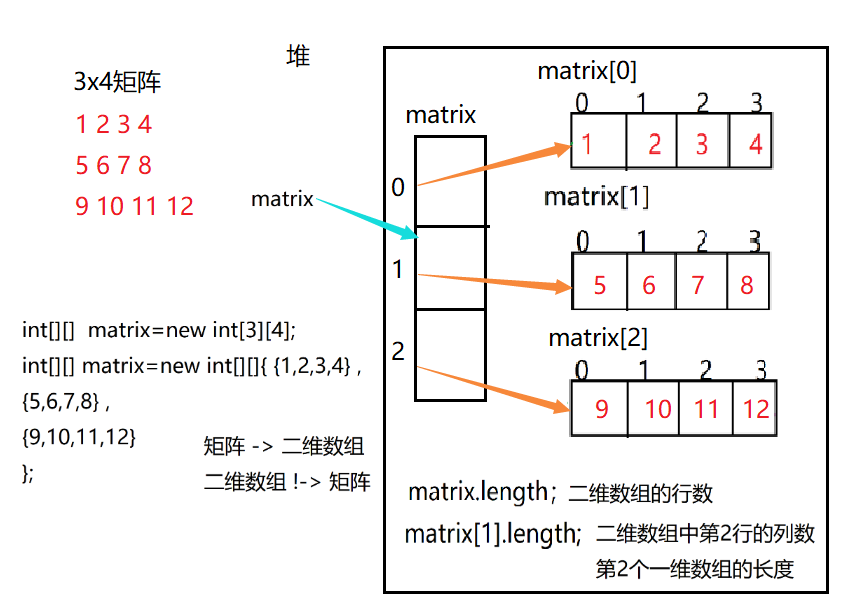
How to create a 2D array?
1.int[][] matrix=new int[3][4];
Create a two-dimensional array with 3 rows and 4 columns, and the elements are all 0 by default
2.int[][] matrix=new int[][]{
{1,2,3,4} ,
{5,6,7,8} ,
{9,10,11,12}
};
Create a 2D array of specified elements
3.int[][] matrix={
{1,2,3,4} ,
{5,6,7,8} ,
{9,10,11,12}
};
4. Sawtooth matrix / 2D array
int[][] matrix={
{1,2,3,4} ,
{5,6,7} ,
{8,9},
{10}
};
In particular, if the rows and columns of a two-dimensional array are equal, it is also called a square array
Here's an example:
matrix.length is the length row number of the outermost one-dimensional array
matrix[i] represents the element of the angle I in the outermost one-dimensional array, but this element is also a one-dimensional array
matrix[i].length represents the length of the one-dimensional array element (the length of the current row)
matrix[i][j] represents the element with the angle J in this one-dimensional array element
class Test01{
public static void main(String[] args){
int[][] matrix={
{1,2,3,4},
{5,6,7,8},
{8,7,6,5},
{4,3,2,1}
};
for(int i=0;i<matrix.length;i++){
for(int j=0;j<matrix[i].length;j++){
System.out.print(matrix[i][j]+" ");
}
System.out.println();
}
}
}Output results:
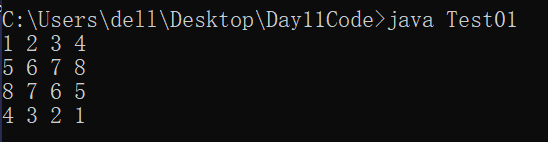
Note: int[][] matrix=new int[m][n]; under this two-dimensional array definition, there are m+1 one-dimensional arrays in memory.
Let's look at a few questions:
First question

Thought analysis:
(0,0) (0,1) (0,2) (0,3)
(1,0) (1,1) (1,2) (1,3)
(2,0) (2,1) (2,2) (2,3)
We will find that when we add rows, the rows will remain the same and the columns will change; when we add columns, the columns will remain the same and the rows will change.
Then we have two steps: 1. Input a 3 * 4 matrix
2. Print the sum of each column
import java.util.*;
class Demo05_09{
public static void main(String[] args){
Scanner scanner=new Scanner(System.in);
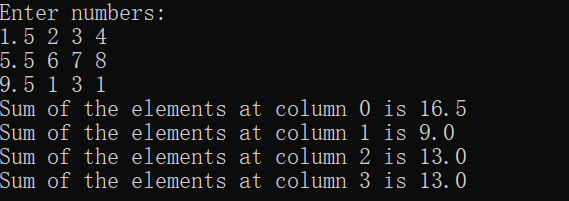
System.out.println("Enter numbers:");
double[][] matrix=new double[3][4];
for(int i=0;i<matrix.length;i++){//1. Input a 3 * 4 matrix
for(int j=0;j<matrix[i].length;j++){
matrix[i][j]=scanner.nextDouble();
}
}
for(int col=0;col<matrix[0].length;col++){//2. Print the sum of each column
System.out.println("Sum of the elements at column "+col+" is "+sumColumn(matrix,col));
}
}
public static double sumColumn(double[][] m,int col){
double sum=0;
for(int row=0;row<m.length;row++){
sum+=m[row][col];
}
return sum;
}
}Results:
Second questions

Analysis:
(0,0) (0,1) (0,2)
(1,0) (1,1) (1,2)
(2,0) (2,1) (2,2)
The elements on the main diagonal are equal
We have also added an additional question to this question, which is to find the sum of the numbers on the sub diagonal, in fact, the method is similar
There are two ways to calculate and. One is to traverse and sum to determine whether the rows and columns are equal, and then calculate and. However, the time complexity is too large, which belongs to the loop nesting of for
The other is direct addition, because this is a square matrix with equal rows and columns. We can directly add elements with equal rows and columns
class Demo05_10{
public static void main(String[] args){
int[][] m={
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10,11,12},
{13,14,15,16}
};
//Main diagonal line
int sum=0;
for(int i=0;i<m.length;i++){
sum+=m[i][i];
}
System.out.println(sum);
//Auxiliary diagonal line
int subsum=0;
for(int i=0;i<m.length;i++){
subsum+=m[i][m.length-1-i];
}
System.out.println(subsum);
/*
for(int i=0;i<m.length;i++){
for(int j=0;j<m[i].length;j++){
if(i==j){
sum+=m[i][j];
}
}
}
*/
}
}Results:

Third questions

Analysis:
m*n * n*p m*p matrix multiplication the column of the former must be equal to the row of the latter
1 2 3 1 2 1*1+2*3+3*5 1*2+2*4+3*6
× 3 4 =
4 5 6 5 6 4*1+5*3+6*5 4*2+5*4+6*6
Step: 1. Input two 2D arrays and define a new array to store the result of multiplication
2. According to the formula given in the question, traverse the calculation
class Demo05_11{
public static void main(String[] args){
double[][] A={ //m*p
{1,2,3},
{4,5,6},
{7,8,9}
};
double[][] B={ //p*n
{0,2.0,4.0},
{1,4.5,2.2},
{1.1,4.3,5.2}
};
double[][] C=new double[A.length][B[0].length];//m*n
for(int i=0;i<C.length;i++){
for(int j=0;j<C[i].length;j++){
double sum=0;
for(int k=0;k<B.length;k++){
sum+=A[i][k]*B[k][j];
}
C[i][j]=sum;
System.out.print(C[i][j]+" ");
}
System.out.println();
}
}
}Results:

Fourth questions

Analysis: we can iterate to compare, but the time complexity is too high, so we can change the way of thinking. We can sum each row, column and diagonal. If the sum is 0, the whole row is 0. and so on.
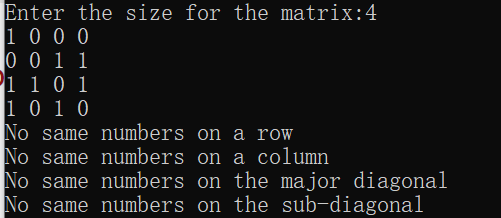
1. Input the dimension of the policy to create a square matrix
2. Randomly fill 0 or 1 into the square matrix
3. Row, column and diagonal accumulation sum==0 sum==size means all equal
import java.util.*;
class Demo05_12{
public static void main(String[] args){
//1. Input the dimension of the policy to create a square matrix
Scanner scanner=new Scanner(System.in);
System.out.print("Enter the size for the matrix:");
int size=scanner.nextInt();
int[][] m=new int[size][size];
//2. Randomly fill 0 or 1 into the square matrix
Random random=new Random();
for(int i=0;i<size;i++){
for(int j=0;j<size;j++){
m[i][j]=random.nextInt(2);
System.out.print(m[i][j]+" ");
}
System.out.println();
}
//3. Make row, column and diagonal sum==0 sum==size means equal
checkRow(m);
checkCol(m);
checkDiagonal(m);
checkSubDiagonal(m);
}
public static void checkSubDiagonal(int[][] m){
int sum=0;
for(int i=0;i<m.length;i++){
sum+=m[i][m.length-1-i];
}
if(sum==m.length||sum==0){
System.out.printf("The minor diagonal lines are all equal and are%d\n",sum==0?0:1);
}
System.out.println("No same numbers on the sub-diagonal");
}
public static void checkDiagonal(int[][] m){
int sum=0;
for(int i=0;i<m.length;i++){
sum+=m[i][i];
}
if(sum==m.length||sum==0){
System.out.printf("The main diagonal is all equal and is%d\n",sum==0?0:1);
}
System.out.println("No same numbers on the major diagonal");
}
public static void checkRow(int[][] m){
for(int i=0;i<m.length;i++){
int sum=0;
for(int j=0;j<m[i].length;j++){
sum+=m[i][j];
}
if(sum==m.length||sum==0){
System.out.printf("All os on row "+(i+1)+" "+(sum==0?0:1));
}
}
System.out.println("No same numbers on a row");
}
public static void checkCol(int[][] m){
for(int j=0;j<m.length;j++){
int sum=0;
for(int i=0;i<m.length;i++){
sum+=m[i][j];
}
if(sum==m.length||sum==0){
System.out.printf("All os on col "+(j+1)+" "+(sum==0?0:1));
}
}
System.out.println("No same numbers on a column");
}
}Results: