1 Introduction

Our common target detection is rectangular box detection, but sometimes the box we detect is an irregular quadrilateral. The following figure is a common remote sensing image. At this time, the way we use rectangular box to calculate IOU is no longer applicable. We can abstract the problem. Is there a way to calculate two irregular quadrilateral IOU?

2 rectangular IOU calculation method

Generally speaking, there are two ways to abstract the target rectangle:

• Top left and bottom right indicate: x1 y1 x2 y2
• Center point: c_x,c_y,w,h

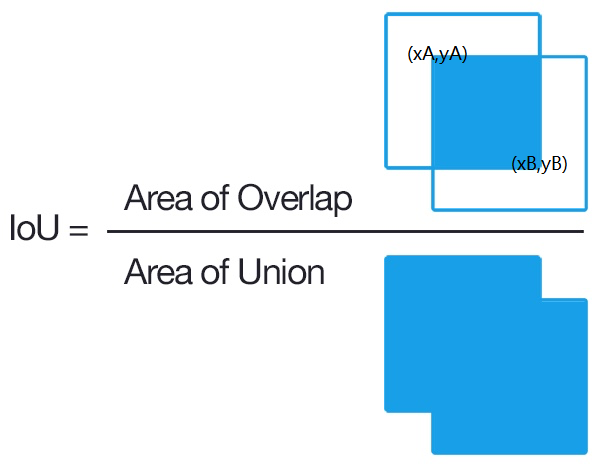
The calculation method of IOU of rectangular box under two representations is as follows:

The IOU calculation code for top left and bottom right is as follows:

def bb_intersection_over_union(boxA, boxB):
    boxA = [int(x) for x in boxA]
    boxB = [int(x) for x in boxB]
    xA = max(boxA[0], boxB[0])
    yA = max(boxA[1], boxB[1])
    xB = min(boxA[2], boxB[2])
    yB = min(boxA[3], boxB[3])
    
    interArea = max(0, xB - xA + 1) * max(0, yB - yA + 1)
    boxAArea = (boxA[2] - boxA[0] + 1) * (boxA[3] - boxA[1] + 1)
    boxBArea = (boxB[2] - boxB[0] + 1) * (boxB[3] - boxB[1] + 1)
    iou = interArea / float(boxAArea + boxBArea - interArea)
    return iou

The explanation is as follows:

• Since the intersection of two rectangular boxes is still rectangular, we first calculate the upper left and lower right coordinates Xa, ya, XB and Yb of the intersection rectangular box
• Calculate the area interArea of the intersection rectangle of two rectangles
• The area of the union of two rectangular boxes can be obtained by using the union of two rectangular boxes = the area of rectangular box A + the area of rectangular box B - the area of the intersection
• The IOU can be obtained by dividing the intersection rectangular area by the union rectangular area

3 calculation method of irregular quadrilateral IOU

Read the calculation method of rectangular IOU above. Since the intersection of rectangular boxes is still rectangular boxes, the calculation of intersection rectangle is relatively simple. Next, let's think about the calculation method of irregular quadrilateral IOU:

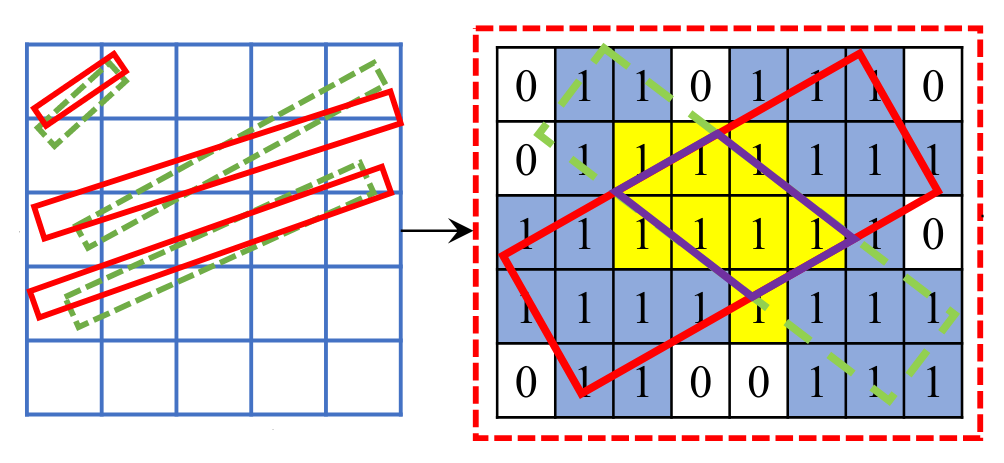
As shown on the right side of the above figure, the red solid line box is the marked true value box, and the front green dotted line box is the prediction box
We can use the number of common pixels between two arbitrary rotation frames to approximate IoU. Considering that the images are plastic coordinates, the area of irregular quadrilateral can be approximately replaced by the number of pixels contained
Based on this, we summarize the IOU calculation steps of any two irregular quadrilaterals as follows:

• step1: generate three all black binary graphs( I A I_A IA​ , I B I_B IB​ , I C I_C IC), length and width are the same as network input
• Step 2: set quadrilateral R e c t A Rect_A RectA ， draw to binary graph I A I_A IA ， and fill with all white, and the pixel value is filled with 255
• step3: set quadrilateral R e c t B Rect_B RectB} draw to binary graph I B I_B IB ， and fill with all white, and the pixel value is filled with 255
• step4: set quadrilateral R e c t A Rect_A RectA} and R e c t B Rect_B RectB ＾ respectively draw to the binary diagram I C I_C IC ， and fill with all white, and the pixel value is filled with 255
• step5: calculate three binary diagrams respectively I A I_A IA​, I B I_B IB​, I C I_C The number of white pixels on IC ￠ is expressed as S u m A Sum_A SumA​, S u m B Sum_B SumB​, S u m C Sum_C SumC​
• step6: calculate the intersection area of two quadrangles A r e a 1 Area_1 Area1​ = S u m A Sum_A SumA​ + S u m B Sum_B SumB​ - S u m C Sum_C SumC​
• step6: calculate the Union area of two quadrangles A r e a 2 Area_2 Area2​ = S u m C Sum_C SumC​
• step7: calculate the intersection and union ratio I o u Iou Iou = A r e a 1 Area_1 Area1​ / A r e a 2 Area_2 Area2​

The above calculation process is shown in the figure below:

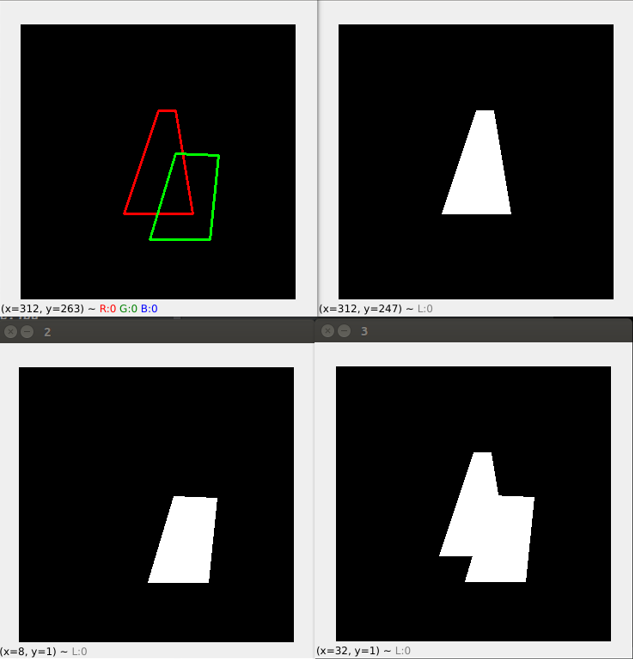As shown in the above figure, the upper left red box is the true value of the quadrilateral, and the green box is the prediction box of the quadrilateral. The upper right shows the filling diagram of the true value box obtained in step 2 above; The lower left shows the filling diagram of the prediction frame obtained in step 3 above; The lower right shows the filling diagram after the union of the prediction box and the truth box obtained in step 4 above

4 code implementation

4.1 generate sample

We assume that our network input is 320X320, the corresponding truth box is rect1, and the corresponding prediction box is rect2. Both are irregular quadrangles, as shown below:

net_width = 320
net_height = 320
rect1 = [160,100, 120,220, 200,220, 180, 100]
rect2 = [180,150, 150,250, 220,250, 230 ,152]

4.2 filling function

Next, we need to fill the truth box and prediction box. Here, we use the fillPoly function to complete the above functions. The code is as follows:

def draw_region(img,rect_1,rect_2=None,fill_value=255):
    pt_list = list()
    for i in range(4):
        pt_list.append((rect_1[i*2],rect_1[i*2+1]))
    cv2.fillPoly(img, [np.array(pt_list)], fill_value)
    if rect_2 is not None:
        pt_list2 = list()
        for i in range(4):
            pt_list2.append((rect_2[i * 2], rect_2[i * 2 + 1]))
        cv2.fillPoly(img, [np.array(pt_list2)], fill_value)
    return img

4.3 calculation of IOU

Next, we count the area of the three filled images, and then we can calculate the intersection and union ratio corresponding to the truth box and the prediction box. The code is as follows:

def compute_iou(net_width,net_height,rect1,rect2,fill_value=255):
    img1 = np.zeros((net_height, net_width), np.uint8)
    img2 = np.zeros((net_height, net_width), np.uint8)
    img3 = np.zeros((net_height, net_width), np.uint8)
    out_img1 = draw_region(img1, rect1, fill_value=fill_value)
    out_img2 = draw_region(img2, rect2, fill_value=fill_value)
    out_img3 = draw_region(img3, rect1, rect2, fill_value=fill_value)
    area_1 = np.sum(out_img1 == fill_value)
    area_2 = np.sum(out_img2 == fill_value)
    area_com = np.sum(out_img3 == fill_value)
    print("area1 ={} area2={} area3={} ".format(area_1, area_2, area_com))
    iou = (area_1 + area_2 - area_com) * 1.0 / area_com
    return iou

The operation results are as follows:

According to the above figure, the intersection union ratio of the two quadrangles in the sample is 0.17

4.4 application

As an example in practical application, as shown in the figure below, the result of parking space detection on the left fish eye image is irregular quadrilateral, and the detection frame with the highest NMS retention confidence needs to be carried out. At this time, the above calculation method of irregular quadrilateral IOU needs to be used for NMS operation

5 Summary

In this paper, the calculation of the intersection and union ratio of two rectangular frames is extended to the calculation of the intersection and union ratio of two irregular quadrangles, and a complete code implementation and corresponding practical application examples are given

4.3 calculating IOU## 4.3 calculating IOU

6 reference

reference resources:

Link one
Link 2