The three basic algorithms of gyro attitude estimation, such as the integral algorithm and the gradient filtering algorithm, are used to realize the attitude estimation of the gyro at the same time, It is necessary to find a sensor that does not change with time to estimate the attitude and calibrate it. The three methods have their own advantages and disadvantages. The complementary and gradient algorithm is more suitable for dealing with aircraft with limited performance, such as micro four-axis, which adopts low-frequency Cortex-M0 or M1 processor. When the conditions permit and the performance is sufficient, it is suggested to consider the algorithm of extended Kalman filter
The improved complementary filtering algorithm is adopted in the PX4 source code. On the basis of the original accelerometer calibration gyroscope, the magnetometer and GPS data are added for further quaternion calibration compensation. Its advantage is simple operation, so it has become the default attitude solution algorithm in PX4
Reference article: [basic algorithm learning 4] complementary filtering algorithm - PX4 attitude estimation
PX4 source code analysis 3: attitude_estimator_q
Firmware version: v1.0 eleven point three
Noun interpretation
gyroscope
gyroscope, which measures angular velocity and has high dynamic characteristics, is a device for indirectly measuring angle. It measures the derivative of the angle, that is, the angular velocity. The angle can be obtained only by integrating the angular velocity with time. Due to the influence of noise and other errors, they accumulate continuously under the action of integration, which eventually leads to the low-frequency interference and drift of gyroscope.
Accelerometer
output the direction of current acceleration (including gravity acceleration g) [also known as gravity sensor]. When hovering, the output is g. The high-frequency signal sensitivity caused by its measurement principle makes the accelerometer have large high-frequency interference in the vibration environment.
Magnetometer (also known as magnetic compass)
the output is the angle between the current body and the geomagnetic field. The measuring principle is similar to that of a compass. It has good low-frequency characteristics and is easy to be disturbed by the surrounding magnetic field.
Reference to the working principle of magnetometer: http://blog.sina.com.cn/s/blog_402c071e0102v8ig.html
Coordinate system
- Navigation coordinate system: in multi rotor, it is also called earth coordinate system and geographic coordinate system. Generally, the North East earth (NED) is used to form the X, y and Z axes of the coordinate system.
- Body coordinate system: fixed on the multi rotor aircraft, that is, the origin of the coordinate system is located at the center point of the aircraft (assuming that the center point coincides with the center of gravity).
For the coordinate system used in aviation navigation, please refer to AIAA series. In the multi rotor, because it only flies at low altitude and the time is short, only the above two are required.
Gesture representation
- Euler angle: it is more intuitive and describes the attitude of rigid body in three-dimensional Euclidean space. At this time, the coordinate system is the body coordinate system, which rotates with the rotation of the rigid body. Disadvantages: universal joint lock.
- Quaternion: a set of four-dimensional vectors representing the three-dimensional rotation of a rigid body. Suitable for computer calculation.
- Direction cosine matrix DCM: the rotation of the coordinate system expressed by the cosine value of Euler angle or quaternion.
Filtering principle
complementary filtering requires the interference noise of the two signals to be at different frequencies. By setting the cut-off frequency of the two filters, it is ensured that the fused signal can cover the required frequency.
in the attitude estimation of IMU, the complementary filter uses high pass filtering for the gyroscope (low-frequency noise); Use low frequency filtering for accelerometer / magnetometer (high frequency noise).
in complementary filtering, the cut-off frequencies of the two filters are the same. At this time, it is necessary to choose them according to the value of useful frequency.
when the body is horizontal, the accelerometer cannot measure the rotation around the Z axis, i.e. yaw angle. The magnetometer has the same problem. It cannot measure the rotation of the magnetic shaft. Therefore, it is necessary to calibrate the gyroscope with accelerometer and magnetometer at the same time.
UAV attitude estimation part
Header file part code
//Call the header file of UAV attitude and parameters #include <float.h> #include <drivers/drv_ hrt. H / / high precision timer. In the control process, most links use the classical PID control algorithm //To obtain the most important time variable of real-time response, which involves how to obtain high-precision time. pixhawk has high-precision RTC (real-time clock) //The header file is introduced #include <lib/ecl/geo/geo.h> #include <lib/ecl/geo_lookup/geo_mag_declination.h> #include <lib/mathlib/mathlib.h> #include <lib/parameters/param.h> #include <matrix/math.hpp> #include <px4_platform_common/defines.h> #include <px4_platform_common/module.h> #include <px4_platform_common/module_params.h> #include <px4_platform_common/posix.h> #include <uORB/Publication.hpp> #include <uORB/Subscription.hpp> #include <uORB/SubscriptionCallback.hpp> #include <uORB/topics/parameter_update.h> #include <uORB/topics/sensor_combined.h> #include <uORB/topics/vehicle_attitude.h> #include <uORB/topics/vehicle_gps_position.h> #include <uORB/topics/vehicle_local_position.h> #include <uORB/topics/vehicle_magnetometer.h> #include <uORB/topics/vehicle_odometry.h>
using keyword
using matrix::Dcmf; using matrix::Eulerf; using matrix::Quatf; using matrix::Vector3f; using matrix::wrap_pi;
**Using keyword: * * indicates that the name is introduced into the declaration area where the using description appears
Class definition
class AttitudeEstimatorQ : public ModuleBase<AttitudeEstimatorQ>, public ModuleParams, public px4::WorkItem
{
public:
AttitudeEstimatorQ();
~AttitudeEstimatorQ() override;
/** @see ModuleBase */
static int task_spawn(int argc, char *argv[]);
/** @see ModuleBase */
static int custom_command(int argc, char *argv[]);
/** @see ModuleBase */
static int print_usage(const char *reason = nullptr);
bool init();//Initialization function
private:
void Run() override;
void update_parameters(bool force = false);
bool init_attq();
bool update(float dt); //dt is the update cycle. This function is the core of the whole program
// Update magnetic declination (in rads) immediately changing yaw rotation
//Update the magnetic yaw angle (in rads) and immediately change the yaw rotation
//When the yaw angle changes, the magnetic azimuth is updated immediately
void update_mag_declination(float new_declination);
const float _eo_max_std_dev = 100.0f; /**< Maximum permissible standard deviation for estimated orientation */
//Maximum allowable standard deviation of estimated azimuth
const float _dt_min = 0.00001f;//dt refers to the time interval of updating data, that is, T in the discrete pid formula
const float _dt_max = 0.02f;
uORB::SubscriptionCallbackWorkItem _sensors_sub{this, ORB_ID(sensor_combined)};
uORB::Subscription _parameter_update_sub{ORB_ID(parameter_update)};
uORB::Subscription _gps_sub{ORB_ID(vehicle_gps_position)};
uORB::Subscription _local_position_sub{ORB_ID(vehicle_local_position)};
uORB::Subscription _vision_odom_sub{ORB_ID(vehicle_visual_odometry)};
//In topicvehicle_ Inside the odometry
uORB::Subscription _mocap_odom_sub{ORB_ID(vehicle_mocap_odometry)};
uORB::Subscription _magnetometer_sub{ORB_ID(vehicle_magnetometer)};
//UAV attitude data release
uORB::Publication<vehicle_attitude_s> _att_pub{ORB_ID(vehicle_attitude)};
int _lockstep_component{-1};
float _mag_decl{0.0f};/**Magnetic azimuth**/
float _bias_max{0.0f};/**Maximum deviation**/
Vector3f _gyro; //Angular velocity of three axes obtained by gyroscope
Vector3f _accel; //Triaxial acceleration obtained by accelerometer
Vector3f _mag; //Magnetic heading obtained by magnetometer
Vector3f _vision_hdg;//Visual position estimation;
Vector3f _mocap_hdg; //vicon attitude position estimation;
Quatf _q; //Quaternion
Vector3f _rates; //Attitude angular velocity and above_ Unlike gyro, this one is used to store the corrected angular velocity around the three axes
Vector3f _gyro_bias; //Gyro deviation
Vector3f _vel_prev; //Previous acceleration
//Absolute time
hrt_abstime _vel_prev_t{0};//The absolute time when calculating the speed at the previous moment is used to calculate the acceleration according to the speed difference divided by the time difference
Vector3f _pos_acc;//Motion acceleration, note: this acceleration does not include the acceleration in the vertical direction
hrt_abstime _last_time{0};
bool _inited{false};//Initialization identification;
bool _data_good{false}; //Data availability;
bool _ext_hdg_good{false};//External heading available;
//Parameter definition
/**w in front means weight**/
DEFINE_PARAMETERS(
(ParamFloat<px4::params::ATT_W_ACC>) _param_att_w_acc, //Accelerometer weight 0.2f
(ParamFloat<px4::params::ATT_W_MAG>) _param_att_w_mag, //Magnetometer weight 0.1f
(ParamFloat<px4::params::ATT_W_EXT_HDG>) _param_att_w_ext_hdg, //External heading weight 0.1f
(ParamFloat<px4::params::ATT_W_GYRO_BIAS>) _param_att_w_gyro_bias, //Gyro deviation weight 0.1f
(ParamFloat<px4::params::ATT_MAG_DECL>) _param_att_mag_decl, //Magnetic declination (°) 0.0f
(ParamInt<px4::params::ATT_MAG_DECL_A>) _param_att_mag_decl_a, //Enable GPS based automatic declination correction 1
(ParamInt<px4::params::ATT_EXT_HDG_M>) _param_att_ext_hdg_m, //External heading mode 0
(ParamInt<px4::params::ATT_ACC_COMP>) _param_att_acc_comp, // Enable acceleration compensation based on GPS speed 1
(ParamFloat<px4::params::ATT_BIAS_MAX>) _param_att_bias_mas, //Upper limit of gyro deviation 0.05f
(ParamInt<px4::params::SYS_HAS_MAG>) _param_sys_has_mag //Vibration level alarm threshold 0.2f
)
};
Parameter definition
//Parameter definition
/**w in front means weight**/
DEFINE_PARAMETERS(
(ParamFloat<px4::params::ATT_W_ACC>) _param_att_w_acc, //Accelerometer weight 0.2f
(ParamFloat<px4::params::ATT_W_MAG>) _param_att_w_mag, //Magnetometer weight 0.1f
(ParamFloat<px4::params::ATT_W_EXT_HDG>) _param_att_w_ext_hdg, //External heading weight 0.1f
(ParamFloat<px4::params::ATT_W_GYRO_BIAS>) _param_att_w_gyro_bias, //Gyro deviation weight 0.1f
(ParamFloat<px4::params::ATT_MAG_DECL>) _param_att_mag_decl, //Magnetic declination (°) 0.0f
(ParamInt<px4::params::ATT_MAG_DECL_A>) _param_att_mag_decl_a, //Enable GPS based automatic declination correction 1
(ParamInt<px4::params::ATT_EXT_HDG_M>) _param_att_ext_hdg_m, //External heading mode 0
(ParamInt<px4::params::ATT_ACC_COMP>) _param_att_acc_comp, // Enable acceleration compensation based on GPS speed 1
(ParamFloat<px4::params::ATT_BIAS_MAX>) _param_att_bias_mas, //Upper limit of gyro deviation 0.05f
(ParamInt<px4::params::SYS_HAS_MAG>) _param_sys_has_mag //Vibration level alarm threshold 0.2f
)
Initialization assignment
//Initialization of data
AttitudeEstimatorQ::AttitudeEstimatorQ() :
ModuleParams(nullptr),
WorkItem(MODULE_NAME, px4::wq_configurations::nav_and_controllers)
{
_vel_prev.zero();/**Clear**/
_pos_acc.zero();
_gyro.zero();
_accel.zero();
_mag.zero();
_vision_hdg.zero();/**Clear the heading obtained by vision**/
_mocap_hdg.zero();/**The heading obtained by mocap is cleared**/
_q.zero();
_rates.zero();
_gyro_bias.zero();
update_parameters(true);
_lockstep_component = px4_lockstep_register_component();
}
Destructor
//Destructor, clear all tasks
AttitudeEstimatorQ::~AttitudeEstimatorQ()
{
px4_lockstep_unregister_component(_lockstep_component);
}
initialization
//Initialization function
bool
AttitudeEstimatorQ::init()
{
if (!_sensors_sub.registerCallback()) {
PX4_ERR("sensor combined callback registration failed!");
return false;
}
return true;
}
Run function
void
AttitudeEstimatorQ::Run()
{
if (should_exit()) {
_sensors_sub.unregisterCallback();
exit_and_cleanup();
return;
}
sensor_combined_s sensors;
//If the parameter is updated, enter the following function
if (_sensors_sub.update(&sensors)) {
//Parameter update
//Update the quaternion according to this deflection angle
update_parameters();
// Feed validator with recent sensor data
//Fill the verifier with recent data for data verification
if (sensors.timestamp > 0) {
_gyro(0) = sensors.gyro_rad[0];
_gyro(1) = sensors.gyro_rad[1];
_gyro(2) = sensors.gyro_rad[2];
}
if (sensors.accelerometer_timestamp_relative != sensor_combined_s::RELATIVE_TIMESTAMP_INVALID) {
_accel(0) = sensors.accelerometer_m_s2[0];
_accel(1) = sensors.accelerometer_m_s2[1];
_accel(2) = sensors.accelerometer_m_s2[2];
//The length function is the square of the sum of squares
if (_accel.length() < 0.01f) {
PX4_ERR("degenerate accel!");
return;
}
}
// Update magnetometer
//If the data is updated, the data is assigned
//The only variables defined in topic are magnetometer_ga[3]
if (_magnetometer_sub.updated()) {
vehicle_magnetometer_s magnetometer;
if (_magnetometer_sub.copy(&magnetometer)) {
_mag(0) = magnetometer.magnetometer_ga[0];
_mag(1) = magnetometer.magnetometer_ga[1];
_mag(2) = magnetometer.magnetometer_ga[2];
if (_mag.length() < 0.01f) {
PX4_ERR("degenerate mag!");
return;
}
}
}
_data_good = true;
// Update vision and motion capture heading
//Update visual and motion capture titles
_ext_hdg_good = false;
if (_vision_odom_sub.updated()) {
vehicle_odometry_s vision;
if (_vision_odom_sub.copy(&vision)) {
// validation check for vision attitude data
//Verification and inspection of visual attitude data
// vision_att_valid is a bool type, which is mainly used to judge, but what does the data in it mean?
bool vision_att_valid = PX4_ISFINITE(vision.q[0])
&& (PX4_ISFINITE(vision.pose_covariance[vision.COVARIANCE_MATRIX_ROLL_VARIANCE]) ? sqrtf(fmaxf(
vision.pose_covariance[vision.COVARIANCE_MATRIX_ROLL_VARIANCE],
fmaxf(vision.pose_covariance[vision.COVARIANCE_MATRIX_PITCH_VARIANCE],
vision.pose_covariance[vision.COVARIANCE_MATRIX_YAW_VARIANCE]))) <= _eo_max_std_dev : true);
//If effective
if (vision_att_valid) {
//Assign the quaternion based on vision to the new math::q
//The transformation matrix is obtained, and the visual quaternion is transformed into the transformation matrix
Dcmf Rvis = Quatf(vision.q);
//This is a North pointing vector. What is 0.4f?
Vector3f v(1.0f, 0.0f, 0.4f);
// Rvis is Rwr (robot respect to world) while v is respect to world.
// Rvis is Rwr (robot's relationship to the world), and v is the relationship to the world.
//v is based on the world coordinates, and dcm is transposed by B -- > E
// Hence Rvis must be transposed having (Rwr)' * Vw
// Therefore, Rvis must be transposed with (RWR) '* VW
// Rrw * Vw = vn. This way we have consistency
// Rrw * Vw = vn. We have consistency
//The meaning of "transfer"
_vision_hdg = Rvis.transpose() * v;/**After transposing and multiplying with v, it reflects the visual vector pointing north**/
// vision external heading usage (ATT_EXT_HDG_M 1)
// Visual external Title Usage
if (_param_att_ext_hdg_m.get() == 1) {
// Check for timeouts on data
// Check data timeout
_ext_hdg_good = vision.timestamp_sample > 0 && (hrt_elapsed_time(&vision.timestamp_sample) < 500000);
}
}
}
}
if (_mocap_odom_sub.updated()) {
vehicle_odometry_s mocap;
if (_mocap_odom_sub.copy(&mocap)) {
// validation check for mocap attitude data
bool mocap_att_valid = PX4_ISFINITE(mocap.q[0])
&& (PX4_ISFINITE(mocap.pose_covariance[mocap.COVARIANCE_MATRIX_ROLL_VARIANCE]) ? sqrtf(fmaxf(
mocap.pose_covariance[mocap.COVARIANCE_MATRIX_ROLL_VARIANCE],
fmaxf(mocap.pose_covariance[mocap.COVARIANCE_MATRIX_PITCH_VARIANCE],
mocap.pose_covariance[mocap.COVARIANCE_MATRIX_YAW_VARIANCE]))) <= _eo_max_std_dev : true);
if (mocap_att_valid) {
Dcmf Rmoc = Quatf(mocap.q);
Vector3f v(1.0f, 0.0f, 0.4f);
// Rmoc is Rwr (robot respect to world) while v is respect to world.
// Hence Rmoc must be transposed having (Rwr)' * Vw
// Rrw * Vw = vn. This way we have consistency
_mocap_hdg = Rmoc.transpose() * v;
// Motion Capture external heading usage (ATT_EXT_HDG_M 2)
if (_param_att_ext_hdg_m.get() == 2) {
// Check for timeouts on data
_ext_hdg_good = mocap.timestamp_sample > 0 && (hrt_elapsed_time(&mocap.timestamp_sample) < 500000);
}
}
}
}
if (_gps_sub.updated()) {
vehicle_gps_position_s gps;
if (_gps_sub.copy(&gps)) {
//Magnetometer
//First, check whether automatic magnetic azimuth acquisition is configured, that is, use the following if
if (_param_att_mag_decl_a.get() && (gps.eph < 20.0f)) {
/* set magnetic declination automatically */
// Automatically set magnetic declination
//Automatically obtain the magnetic azimuth. If configured, use the current longitude and latitude
// Through get_ mag_ The declination (_gpos. Lat, _gpos. Lon) function obtains the magnetic declination of the current position
update_mag_declination(get_mag_declination_radians(gps.lat, gps.lon));
}
//If configured, the current magnetic declination is used
}
}
// Local location update
if (_local_position_sub.updated()) {
vehicle_local_position_s lpos;
if (_local_position_sub.copy(&lpos)) {
//Accelerometer
//Obtain the body acceleration and calculate the body acceleration by calculating the speed
//First judge whether the location information is valid
if (_param_att_acc_comp.get() && (hrt_elapsed_time(&lpos.timestamp) < 20_ms)
&& lpos.v_xy_valid && lpos.v_z_valid && (lpos.eph < 5.0f) && _inited) {
/* position data is actual */
const Vector3f vel(lpos.vx, lpos.vy, lpos.vz);
/* velocity updated */
if (_vel_prev_t != 0 && lpos.timestamp != _vel_prev_t) {
float vel_dt = (lpos.timestamp - _vel_prev_t) / 1e6f;
/* calculate acceleration in body frame */
// Acceleration of computer body
// Calculate the acceleration of motion in e system, here pos_acc is very important and should be used for the calibration of the rear accelerometer
_pos_acc = _q.conjugate_inversed((vel - _vel_prev) / vel_dt);
}
_vel_prev_t = lpos.timestamp;//Prepare for iteration
//The last time is to assign the updated data to a variable
_vel_prev = vel;
} else {
/**Otherwise, the position information is outdated and the acceleration information is cleared**/
/* position data is outdated, reset acceleration */
// Reset the data without updating_ vel_ prev_ When the initial value of this variable is 0, the update will replace the data with LPOS Timestamp, which is assigned to 0 without updating
_pos_acc.zero();
_vel_prev.zero();
_vel_prev_t = 0;
}
}
}
/* time from previous iteration */
// Time since last iteration
hrt_abstime now = hrt_absolute_time();
//Conditional expression from right to left
//The following constrain t function is used to limit the action. The qualification rule is: return (Val < min_val)? min_ val : ((val > max_val) ? max_ val : val);
const float dt = math::constrain((now - _last_time) / 1e6f, _dt_min, _dt_max);
_last_time = now;
if (update(dt)) {
vehicle_attitude_s att = {};
att.timestamp = sensors.timestamp;
_q.copyTo(att.q);
/* the instance count is not used here */
// Instance counting is not used here
_att_pub.publish(att);
//Finally, it was released to vehicle_attitude, which corresponds to what we said at the beginning. We can't directly regard the data of gyroscope as attitude information, but
//It can only be used after our treatment. Vehicle_ The information flow of attitude is: sensor combined is subscribed and vehicle attitude is published
}
px4_lockstep_progress(_lockstep_component);
}
}
Parameter update
//Check whether the parameter is updated, false check whether the parameter is updated, true get the parameter, and update the quaternion by the magnetic declination
void
AttitudeEstimatorQ::update_parameters(bool force)
{
// check for parameter updates
if (_parameter_update_sub.updated() || force) {
// clear update
/**Create a construct pupdate, which has the update time, whether to update and fill in information**/
parameter_update_s pupdate;
_parameter_update_sub.copy(&pupdate);
// update parameters from storage
// Update parameters from storage
updateParams();
// disable mag fusion if the system does not have a mag
// If the system does not have blocks, block fusion is disabled
if (_param_sys_has_mag.get() == 0) {
_param_att_w_mag.set(0.0f);
}
// if the weight is zero (=mag disabled), make sure the estimator initializes
// If the weight is zero (= mag disabled), make sure the estimator is initialized
if (_param_att_w_mag.get() < FLT_EPSILON) {
_mag(0) = 1.f;
_mag(1) = 0.f;
_mag(2) = 0.f;
}
// math::radians converts angles to radians
update_mag_declination(math::radians(_param_att_mag_decl.get()));
}
}
Vector computing tips
| name | Standard product / inner product / quantity product / dot product | Vector product / outer product / vector product / cross product |
|---|---|---|
| Operation formula | a·b=|a||b|·cosθ | a × b=c, where | c | = | a | B | sin θ, The direction of c follows the right-hand rule |
| Geometric meaning | The product of the projection of vector a in the direction of vector b and the module of vector b | c is the plane perpendicular to a and b, and expressed as | b · sin θ Is the area of a parallelogram with height and | a | as the bottom |
| Difference of operation results | Scalar (often used in Physics) / quantity (often used in Mathematics) | Vector (often used in Physics) / vector (often used in Mathematics) |
**Vector normalization: * * one is to change the number between (0, 1) decimal One is to change the dimensional expression into Dimensionless expression. Mainly for data processing It's convenient to bring it up. Put it data Mapping to the range of 0 ~ 1 is more convenient and fast.
eg: {2.5 3.5 0.5 1.5} normalized to {0.3125 0.4375 0.0625 0.1875}
Solution: 2.5 + 3.5 + 0.5 + 1.5 = 8,
2.5/8=0.3125,
3.5/8=0.4375,
0.5/8=0.0625,
1.5/8=0.1875.
This normalization is to change the sum in parentheses into 1, and then write the proportion of each number.
Initialize attitude estimation
/***********init_attq() Function function: the rotation matrix and quaternion are initialized by accelerometer and magnetometer**************/
bool
AttitudeEstimatorQ::init_attq()
{
// Rotation matrix can be easily constructed from acceleration and mag field vectors
// The rotation matrix can be easily constructed from acceleration and magnetic field vectors
// 'k' is Earth Z axis (Down) unit vector in body frame
// 'k' is the unit vector of the earth's Z-axis (Down) in the volume frame
//The triaxial acceleration k obtained by the acceleration sensor is the direction vector of acceleration. When the UAV is stable, that is, there is no yaw
Vector3f k = -_accel;
//_ accel has been subscribed in Run(), and is assigned
//k is the acceleration direction vector measured by the acceleration sensor. Since the UAV is generally in a steady state and no motion state when measuring the data for the first time,
//Therefore, the measured acceleration can be directly regarded as the gravitational acceleration g, which is taken as the third row k of dcm rotation matrix
//k is a downward vector
k.normalize();//Vector normalization is the vector divided by its length
// 'i' is Earth X axis (North) unit vector in body frame, orthogonal with 'k'
// 'i' is the unit vector of the earth's X-axis (North) in the volume frame, which is orthogonal to 'k'.
Vector3f i = (_mag - k * (_mag * k));
//Schmidt orthogonalization is explained in the preface
//Schmidt orthogonalization, forcing i to be perpendicular to K; Since the vector k has been normalized, the denominator is equal to 1;
//Here_ mag refers to the north, so the R obtained below is the default, and the aircraft nose also refers to the north
//i is the vector facing north
i.normalize(); //Vector normalization is the vector divided by its length
// 'j' is Earth Y axis (East) unit vector in body frame, orthogonal with 'k' and 'i'
// 'j' is the unit vector of the earth's Y axis (East) in the e coordinate, orthogonal to 'k' and 'i'.
//j is the vector facing east
Vector3f j = k % i;
// Fill rotation matrix
Dcmf R; //3 X 3 rotation matrix
R.row(0) = i;//North fills the i vector in the first row of the matrix
R.row(1) = j;//Fill the j vector in the second row of the matrix
R.row(2) = k;//Next, fill the k vector into the third row of the matrix. Note: from here, we can see that the rotation matrix is b-system to n-system
// Convert to quaternion
// Convert R matrix to Quaternion
_q = R;
// Compensate for magnetic declination compensates the magnetic azimuth of the aircraft, because the previous q is the default aircraft pointing north, but the aircraft does not necessarily point north when taking off
Quatf decl_rotation = Eulerf(0.0f, 0.0f, _mag_decl); /**The rotation matrix is expressed only by the quaternion of yaw**/
_q = _q * decl_rotation;
_q.normalize(); /**Normalization**/ /**q at this point is the real initial q**/
if (PX4_ISFINITE(_q(0)) && PX4_ISFINITE(_q(1)) && /**Judge whether it diverges**/
PX4_ISFINITE(_q(2)) && PX4_ISFINITE(_q(3)) &&
_q.length() > 0.95f && _q.length() < 1.05f) {
_inited = true; /**Initialization complete**/
} else {
_inited = false; /**Initialization failed**/
}
return _inited;
}
Update and update quaternion
//Initialization occurs only once
bool
AttitudeEstimatorQ::update(float dt)
{
if (!_inited) {
if (!_data_good) { /**In the previous Run() function, if the sensor data subscription is normal, the data_good is true**/
return false;
}
return init_attq();
/**Initialize without initialization (premise: sensor data subscription is normal)**/
//Note that init is executed only once in a flight trampoline,
// After the aircraft passes through the Kutta method, the output angle of the aircraft needs to be calculated by init_ Finding transformation matrix by attq
}
/**Previous init_ When attq is completed, continue to execute**/
Quatf q_last = _q; /**Note: quaternion_ q already has content. Here's q_ The function of last is to get a backup for q, which can be seen from the last if**/
// Angular rate of correction
Vector3f corr;
//_ gyro is the result of the assignment of Run() above
float spinRate = _gyro.length(); /**Define a variable: rotation rate, and the length function is the square of the sum of squares**/
//First, judge what mode is used for correction, such as vision, mocap, acc and mag. here we focus on the analysis of using acc and MAG for correction, and the other two are the same
if (_param_att_ext_hdg_m.get() > 0 && _ext_hdg_good) {
if (_param_att_ext_hdg_m.get() == 1) {
// Vision heading correction modifies the vision based heading mode
// Project heading to global frame and extract XY component
Vector3f vision_hdg_earth = _q.conjugate(_vision_hdg); /**Convert b system to e system**/
float vision_hdg_err = wrap_pi(atan2f(vision_hdg_earth(1), vision_hdg_earth(0)));
// Project correction to body frame
corr += _q.conjugate_inversed(Vector3f(0.0f, 0.0f, -vision_hdg_err)) * _param_att_w_ext_hdg.get();
}
if (_param_att_ext_hdg_m.get() == 2) {
// Mocap heading correction
// Project heading to global frame and extract XY component
Vector3f mocap_hdg_earth = _q.conjugate(_mocap_hdg);
float mocap_hdg_err = wrap_pi(atan2f(mocap_hdg_earth(1), mocap_hdg_earth(0)));
// Project correction to body frame
corr += _q.conjugate_inversed(Vector3f(0.0f, 0.0f, -mocap_hdg_err)) * _param_att_w_ext_hdg.get();
}
}
//Magnetometer calibration external navigation failure or not in use
//Convert the magnetometer reading from the body coordinate system to the navigation coordinate system
if (_param_att_ext_hdg_m.get() == 0 || !_ext_hdg_good) {
// Magnetometer correction
// Project mag field vector to global frame and extract XY component
// Project the mag field vector to the global frame and extract the XY component
Vector3f mag_earth = _q.conjugate(_mag); /**Convert b system to e system**/ //The formula is shown in figure-1
//Only vector < 3 > MAG is considered_ Data MAG of the first two dimensions in earth_ Earth (1) and mag_earth(0) (i.e. x, y, ignoring the offset on the z axis), through
//arctan (mag_earth (1), MAG_ The angle obtained by Earth (0)) is different from the magnetic azimuth obtained by longitude and latitude to obtain the error angle mag_err
//wrap_pi function is used to limit the result from - pi to PI. If it is greater than PI, it will make up with 2pi, and if it is less than - pi, it will make up with 2pi
//Note 1: here, the correction method of gps calibration is used to correct the magnetic timing, that is, subtract the automatically obtained magnetic declination from the following. No gps calibration method (see my ppt)
//Note 2: the correction method here is to use the difference between the magnetic declination calculated by the magnetometer and that obtained by gps, and then convert it to b system.
float mag_err = wrap_pi(atan2f(mag_earth(1), mag_earth(0)) - _mag_decl);
//atan2f: 2 indicates two input parameters; Support angle conversion within four quadrants; Output radian value;
//Convert the reading of magnetometer from vector to angle; The magnetic deviation is obtained by subtracting the magnetic deviation from the angle;
//_ mag_decl is obtained by GPS;
float gainMult = 1.0f;
const float fifty_dps = 0.873f;
//float spinRate = _gyro.length(); /** Define a variable: rotation rate, and the length function is the square of the sum of squares**/
if (spinRate > fifty_dps) {
gainMult = math::min(spinRate / fifty_dps, 10.0f);
}
// Project magnetometer correction to body frame
//The following * vector < 3 > (0.0F, 0.0F, - mag_err)) is the level at which raw should essentially be generated by the magnetometer
// The magnetic vector is obtained by cross multiplication with the horizontal magnetic vector generated by gps, and the cross multiplication is just down
//Convert the magnetic field deviation to the body coordinate system and multiply it by its corresponding weight;
//Figure 2
corr += _q.conjugate_inversed(Vector3f(0.0f, 0.0f, -mag_err)) * _param_att_w_mag.get() * gainMult;
}
_q.normalize();//The normalization here is used to correct the update_ mag_ Deviation after declination.
// Accelerometer correction
// Project 'k' unit vector of earth frame to body frame
// Vector3f k = _q.conjugate_inversed(Vector3f(0.0f, 0.0f, 1.0f)); // From n-series to b-series
// Optimized version with dropped zeros
//The following k is obtained by converting the unit vector of gravity in n system into b system, that is, left multiplying the rotation matrix
Vector3f k(
2.0f * (_q(1) * _q(3) - _q(0) * _q(2)),
2.0f * (_q(2) * _q(3) + _q(0) * _q(1)),
(_q(0) * _q(0) - _q(1) * _q(1) - _q(2) * _q(2) + _q(3) * _q(3))
);
//The direction of g is obtained by subtracting the direction of body acceleration (_pos_acc) from the direction of total resultant force (_accel), that is, the gravitational acceleration is obtained by subtracting the body motion acceleration from the total acceleration (acceleration acquisition)
//The direction of gravity acceleration is the z axis under the navigation coordinate system. After adding the motion acceleration, the direction of the total acceleration is not parallel to the sky or ground of the navigation coordinate system, so this error should be eliminated, that is "_accel-_pos_acc"
//Here, multiplied by the difference k, we get the angle sinx with the direction of gravity, which is about equal to x, that is, roll and pitch
// If we are not using acceleration compensation based on GPS velocity,
// fuse accel data only if its norm is close to 1 g (reduces drift). Only when its norm is close to 1 g (reducing drift), acel data can be fused.
const float accel_norm_sq = _accel.norm_squared();
const float upper_accel_limit = CONSTANTS_ONE_G * 1.1f;
const float lower_accel_limit = CONSTANTS_ONE_G * 0.9f;
if (_param_att_acc_comp.get() || ((accel_norm_sq > lower_accel_limit * lower_accel_limit) &&
(accel_norm_sq < upper_accel_limit * upper_accel_limit))) {
// %It means cross multiplication
//Vector k is the gravitational acceleration vector (0,0,1) converted to the body coordinate system;
//_ accel is the reading of accelerometer;
//_ pos_acc is the acceleration derived from the differential of position estimation (GPS);
//_ accel - _pos_acc represents the acceleration vector of the aircraft minus its horizontal component;
//Cross multiply k with (_accel - _pos_acc) to obtain the deviation;
//See figure-3 for the formula
//Here is another understanding
//The direction of g is obtained by subtracting the body acceleration direction (_pos_acc) from the total resultant force direction (_accel), that is, the total acceleration (acceleration acquisition) minus the body motion acceleration to obtain the gravity acceleration, and then the attitude matrix is either row or column to cross product with the pure gravity acceleration to calculate the error. Because motion acceleration is harmful interference, it must be reduced. The theoretical basis of the algorithm is the multiplication of [0,0,1] and attitude matrix.
//The direction of the gravitational acceleration obtained by the difference is the Z axis under the navigation coordinate system. After adding the motion acceleration, the direction of the total acceleration is not parallel to the sky or ground of the navigation coordinate system, so this error should be eliminated, that is "_accel-_pos_acc". Then cross multiply the z-axis vector to get the error and calibrate it.
corr += (k % (_accel - _pos_acc).normalized()) * _param_att_w_acc.get();
}
// Gyro bias estimation
//spinRate rotation rate
if (spinRate < 0.175f) {
//Get the gyro correction value
//Here, the correction value is the integral part of the pi controller of mahony filter;
//Because_ gyro_bias does not return to zero, so it continues to accumulate;
//The formula is shown in figure-4
_gyro_bias += corr * (_param_att_w_gyro_bias.get() * dt); //Corresponding integral control
//Right_ gyro_bias does constraint processing.
for (int i = 0; i < 3; i++) {
_gyro_bias(i) = math::constrain(_gyro_bias(i), -_bias_max, _bias_max);
}
}
_rates = _gyro + _gyro_bias; //Angular velocity = measured value of gyroscope + error calibration Figure 5
// Feed forward gyro
// Embodiment of pi controller, corresponding to proportional part
corr += _rates; //Corr is a variable defined in the update function, so the data of the corr variable will be refreshed every time you enter the update() function
//Here, corr = (Ea+Em) + (Ea+Em)*dt + gyro;
//Personally, I think the corr here is the updated angular velocity;
//See the formula in Figure 6
// Apply correction to state
//Finally, update the quaternion with the corrected data and_ rates and_ gyro_bias is set to zero for the next call.
_q += _q.derivative1(corr) * dt;//Updating quaternions by Runge Kutta method
//Update the quaternion, derivative is the derivative function, and use the first-order Runge Kutta derivative. See figure-6 for the formula
// Normalize quaternion
_q.normalize();
//If the quaternion is not appropriate, reset it
if (!(PX4_ISFINITE(_q(0)) && PX4_ISFINITE(_q(1)) &&
PX4_ISFINITE(_q(2)) && PX4_ISFINITE(_q(3)))) {
// If the data is not suitable, restore the q of the backup, that is, q_last
// Reset quaternion to last good state
// Resets the quaternion to the last good state
_q = q_last;
_rates.zero();
_gyro_bias.zero();
return false;
}
return true;
}
//After updating the quaternion, we jump to the place where the update function is called, that is, line 422. We find that the updated attitude information has been released later. This is the end of the whole process
// The calling function is
// if (update(dt)) {
//}
The above formulas are as follows:
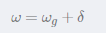
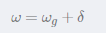
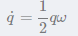
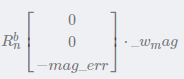

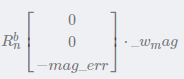
Update yaw angle
/**When the yaw angle changes, the magnetic azimuth is updated immediately**/
void
AttitudeEstimatorQ::update_mag_declination(float new_declination)
{
// Apply initial declination or trivial rotations without changing estimation
// Ignore small rotation (such as small vibration of the body) and continue to use the previous magnetic azimuth
if (!_inited || fabsf(new_declination - _mag_decl) < 0.0001f) {
_mag_decl = new_declination;
} else {
//When the rotation is large, correct the attitude (q) and update the magnetic azimuth
// Immediately rotate current estimation to avoid gyro bias growth
Quatf decl_rotation = Eulerf(0.0f, 0.0f, new_declination - _mag_decl);
// The quaternion generated by yaw angle is generated by making the other two angles 0 and using the Euler angle to quaternion formula
_q = _q * decl_rotation;
//Here, the multiplication of two quaternions indicates the addition of angles. Since q1*q2 represents the synthesis action of q1q2 mathematically, quaternions are corrected here
_mag_decl = new_declination;
//Use new magnetic declination
}
}
Some configuration functions
int
AttitudeEstimatorQ::custom_command(int argc, char *argv[])
{
return print_usage("unknown command");
}
int
AttitudeEstimatorQ::task_spawn(int argc, char *argv[])
{
AttitudeEstimatorQ *instance = new AttitudeEstimatorQ();
if (instance) {
_object.store(instance);
_task_id = task_id_is_work_queue;
if (instance->init()) {
return PX4_OK;
}
} else {
PX4_ERR("alloc failed");
}
delete instance;
_object.store(nullptr);
_task_id = -1;
return PX4_ERROR;
}
int
AttitudeEstimatorQ::print_usage(const char *reason)
{
if (reason) {
PX4_WARN("%s\n", reason);
}
PRINT_MODULE_DESCRIPTION(
R"DESCR_STR(
### Description
Attitude estimator q.
)DESCR_STR");
PRINT_MODULE_USAGE_NAME("AttitudeEstimatorQ", "estimator");
PRINT_MODULE_USAGE_COMMAND("start");
PRINT_MODULE_USAGE_DEFAULT_COMMANDS();
return 0;
}
extern "C" __EXPORT int attitude_estimator_q_main(int argc, char *argv[])
{
return AttitudeEstimatorQ::main(argc, argv);
}
Follow up to add