About Berlin noise:
First paste a paragraph about Baidu Encyclopedia:
Perlin noise refers to the natural noise generation algorithm invented by Ken Perlin. A noise function is basically a seed random generator. It takes an integer as a parameter, and then returns a random number based on this parameter. If the same parameter is passed in twice, it will produce the same number twice. This rule is very important, otherwise the Berlin function just generates a pile of garbage
However, Baidu Encyclopedia does not have more specific steps and processes for the realization of Berlin noise, but Wikipedia introduces the general steps of Berlin noise generation:

The whole process is briefly divided into three parts:
- Select random points and give random values
- Gradient of a given point (identified by interpolation function)
- The value of the assigned position is calculated according to the value and gradient of the random point
In this process, Perlin Noise uses some special processing strategies to ensure that the generated data is pseudo-random and continuous
Simple interpretation of one-dimensional Berlin noise:
According to the steps described in Wikipedia, let's deduce the creation process of one-dimensional Berlin noise:
First, create a coordinate system, with the X axis as the one-dimensional coordinate reference point and the Y axis as the coordinate reference value, so as to create a basic coordinate system
First, select some positions on a one-dimensional array and assign them random values. At the middle of these points, you need to obtain the values through some interpolation algorithms, and finally obtain a continuous curve
In the above process, there are several key points:
- How to select the location of assignment
- How to assign a value to it
- Which interpolation method is used to obtain the value of non integer points
In the case of one-dimensional noise generation, we can obtain these points by rounding at intervals according to the X coordinate axis, and then assign values to these integer points by random method. Next, the corresponding values can be calculated through the numerical interpolation of two adjacent integers at non integer points, so as to obtain a continuous curve, that is, a one-dimensional Berlin noise diagram. Simply write a code to draw a coordinate axis, and draw one-dimensional Berlin noise based on Line Renderer:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class PerlinNoise : MonoBehaviour
{
public int lineWight;
//public List<Vector3> points;
public GameObject posPre;
public Dictionary<int, Vector3> points = new Dictionary<int, Vector3>();
public LineRenderer line;
public int interIndexMax = 100;
private void Awake()
{
CreatePos();
CreateLine();
}
//Draw the numerical point corresponding to the integer point
void CreatePos()
{
for (int i = 0; i < lineWight; i++)
{
float num = Random.Range(0f, 4f);
Vector3 pointPos = new Vector3(i, num, 0);
GameObject go = Instantiate(posPre, this.transform);
go.transform.position = pointPos;
points.Add(i, pointPos);
}
}
//Interpolation between two adjacent integer points to obtain other position values
void CreateLine()
{
int posIndex = 0;
int interIndex;
line.positionCount= interIndexMax * (points.Count - 1);
for (int i = 1; i < points.Count; i++)
{
interIndex = 0;
while (interIndex< interIndexMax)
{
interIndex++;
float posY = points[i - 1].y + (points[i].y - points[i - 1].y) * (interIndex / (float)interIndexMax);
Vector3 pos = new Vector3(i - 1 + interIndex / (float)interIndexMax, posY, 0);
line.SetPosition(posIndex, pos);
posIndex++;
}
}
}
In the above code, it can be seen that a linear interpolation will be performed between two adjacent integer points to find the specific curve between the two points. After running the code, you can see the following effects:
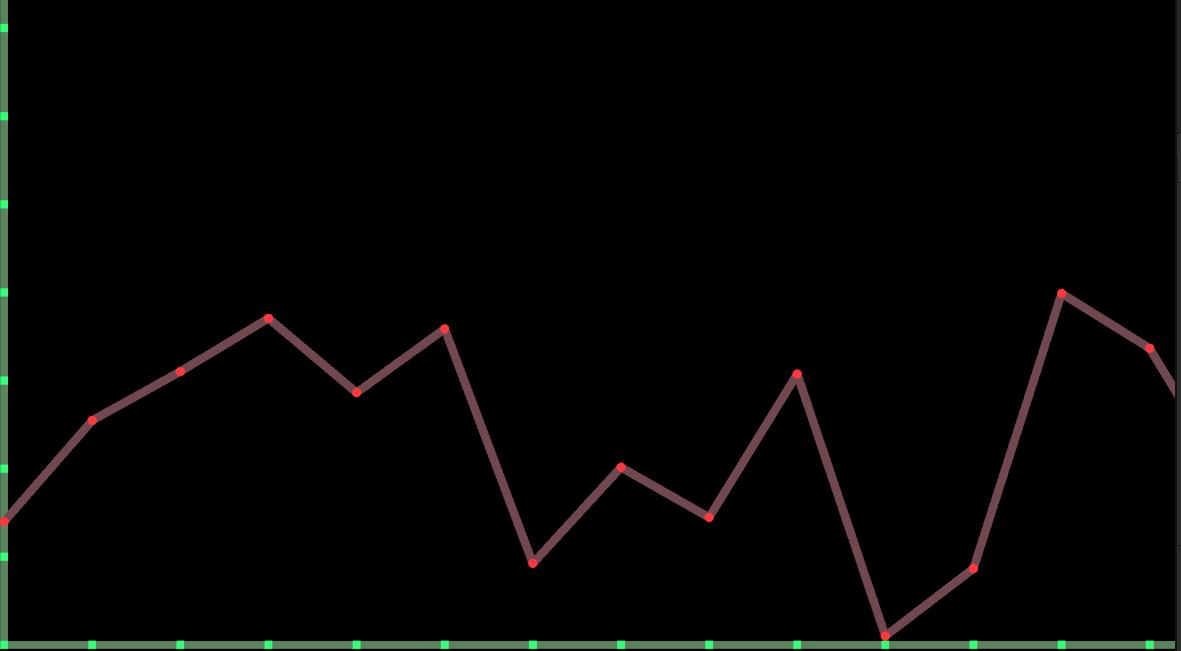
In the above one-dimensional Berlin noise generation, we obtained a continuous polyline based on linear interpolation, because the program will perform a linear interpolation between two adjacent integer points to obtain the coordinates of the middle point. Results a straight line is obtained, and different interpolation intervals are used on the left and right sides of an integer point. As a result, the slopes of the curves on both sides are different at the integer point, resulting in the discontinuity of the one-dimensional curve generated by Perlin Noise at the integer point
In order to avoid the above situation and make the Perlin Noise smoother and more natural, Ken Perlin recommends: 3 t 2 − 2 t 3 {\displaystyle 3t^{2}-2t^{3}} 3t2 − 2t3 is used as the interpolation function of Perline Noise, and in the latest version of the algorithm, the interpolation function is replaced with 6 t 5 − 15 t 4 + 10 t 3 {\displaystyle 6t^{5}-15t^{4}+10t^{3}} 6t5−15t4+10t3
In order to better understand these two interpolation functions, first look at the generated curve effect through the visual code. The first is 3 t 2 − 2 t 3 {\displaystyle 3t^{2}-2t^{3}} For the display effect of 3t2 − 2t3 interpolation function, we simply modify the interpolation method and update the code at the line drawing interpolation:
//Interpolation between two adjacent integer points to obtain other position values
void CreateLine()
{
int posIndex = 0;
int interIndex;
line.positionCount = interIndexMax * (points.Count - 1);
for (int i = 1; i < points.Count; i++)
{
interIndex = 0;
while (interIndex< interIndexMax)
{
interIndex++;
float posY = Mathf.Lerp(points[i - 1].y, points[i].y, InterpolationCalculation(interIndex / (float)interIndexMax));
Vector3 pos = new Vector3(i - 1 + interIndex / (float)interIndexMax, posY, 0);
line.SetPosition(posIndex, pos);
posIndex++;
}
}
}
//Calculation of interpolation function
float InterpolationCalculation(float num)
{
return 3*Mathf.Pow(num, 2)-2*Mathf.Pow(num,3);
}
In the above code, a function calculation formula is simply encapsulated, and then a mapping from the interval range of two integer points to (0, 1) is made through linear interpolation. The final curve is:
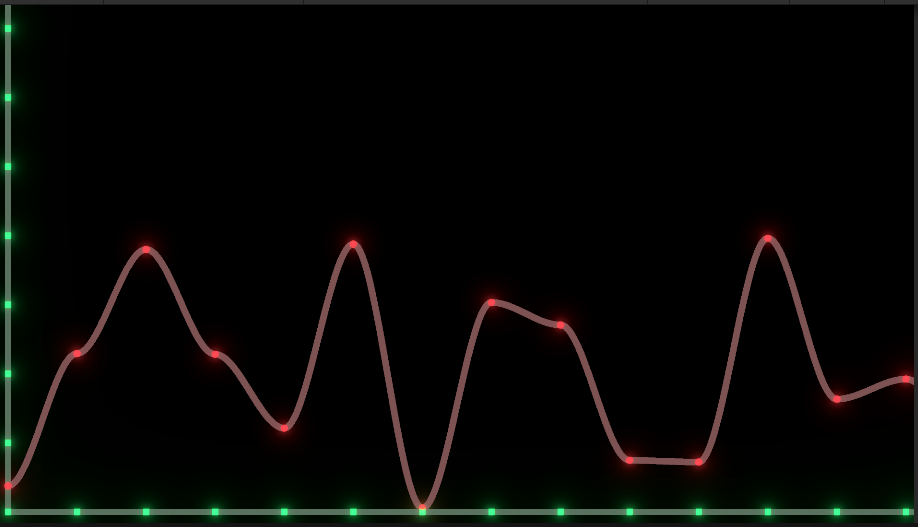
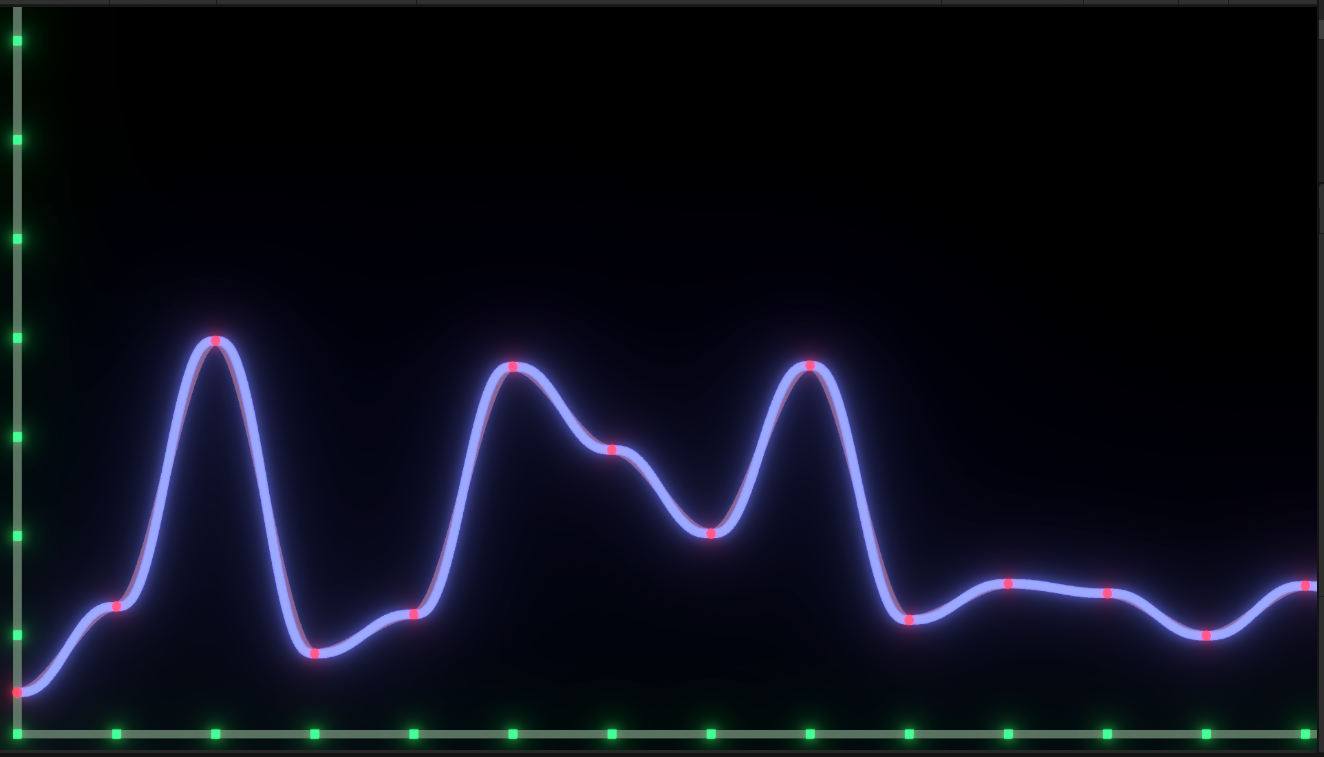
Compared with linear interpolation, the whole curve is significantly smoother, and due to the interpolation function 3 t 2 − 2 t 3 {\displaystyle 3t^{2}-2t^{3}} 3t2 − 2t3 when x is 0 and 1, the corresponding coordinate point slope is 0, so the final interpolation curve is continuous at the integer point, but it still looks sharp at the integer point. Therefore, in the latest Perlin Noise generation algorithm, the interpolation function is replaced with 6 t 5 − 15 t 4 + 10 t 3 {\displaystyle 6t^{5}-15t^{4}+10t^{3}} 6t5 − 15t4+10t3, the following figure shows the comparison of noise curves obtained by two curve interpolation functions:
- Blue curve: represents 6 t 5 − 15 t 4 + 10 t 3 {\displaystyle 6t^{5}-15t^{4}+10t^{3}} Noise curve obtained by 6t5 − 15t4+10t3
- Red curve: represents 3 t 2 − 2 t 3 {\displaystyle 3t^{2}-2t^{3}} 3t2 − 2t3 acquired noise curve
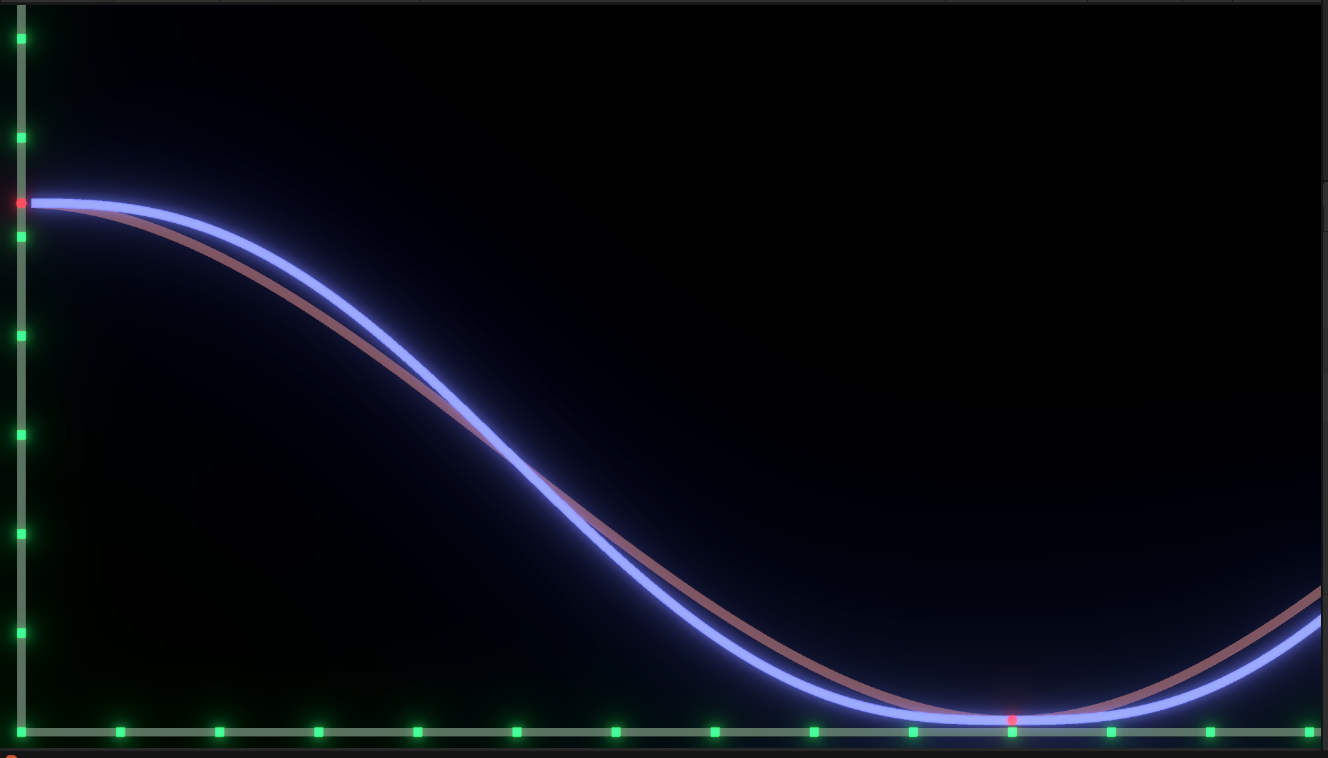
Because the value is too small, the comparison is not very obvious, so we can obviously see by enlarging the X-axis 6 t 5 − 15 t 4 + 10 t 3 {\displaystyle 6t^{5}-15t^{4}+10t^{3}} The slope of the curve obtained by 6t5 − 15t4+10t3 interpolation at the point near the integer point is obviously less than 3 t 2 − 2 t 3 {\displaystyle 3t^{2}-2t^{3}} 3t2 − 2t3 interpolation function, as shown in the figure below:
Deduction of two-dimensional Berlin noise
Considering the generation of two-dimensional Perlin Noise based on one-dimensional Berlin noise, we also need to select integer points of coordinates to give random values, and then adopt corresponding interpolation strategies to obtain the values of non integer values according to the values of these integer points. The whole process is divided into three parts:
Similar to one-dimensional Perlin Noise, two-dimensional Perlin Noise takes integer points for X-axis and Y-axis respectively
Create a three-dimensional coordinate system in the scene, take the plane composed of X axis and Z axis as the two-dimensional coordinate points, and Y axis represents the value of each coordinate:
public int posNumber;
public GameObject posPre;
public LineRenderer line1;
public LineRenderer line2;
public LineRenderer line3;
private void Awake()
{
Coordinate();
}
void Coordinate()
{
line1.positionCount=posNumber;
line2.positionCount=posNumber;
line3.positionCount = posNumber;
for (int i = 0; i < posNumber; i++)
{
GameObject goX = Instantiate(posPre, this.transform);
goX.transform.position = new Vector3(i, 0, 0);
line1.SetPosition(i, new Vector3(i, 0, 0));
GameObject goY = Instantiate(posPre, this.transform);
goY.transform.position = new Vector3(0, i, 0);
line2.SetPosition(i, new Vector3(0, i, 0));
GameObject goZ = Instantiate(posPre, this.transform);
goZ.transform.position = new Vector3(0, 0, i);
line3.SetPosition(i, new Vector3(0, 0, i));
}
}
Execute the code, and the effect is shown as follows:
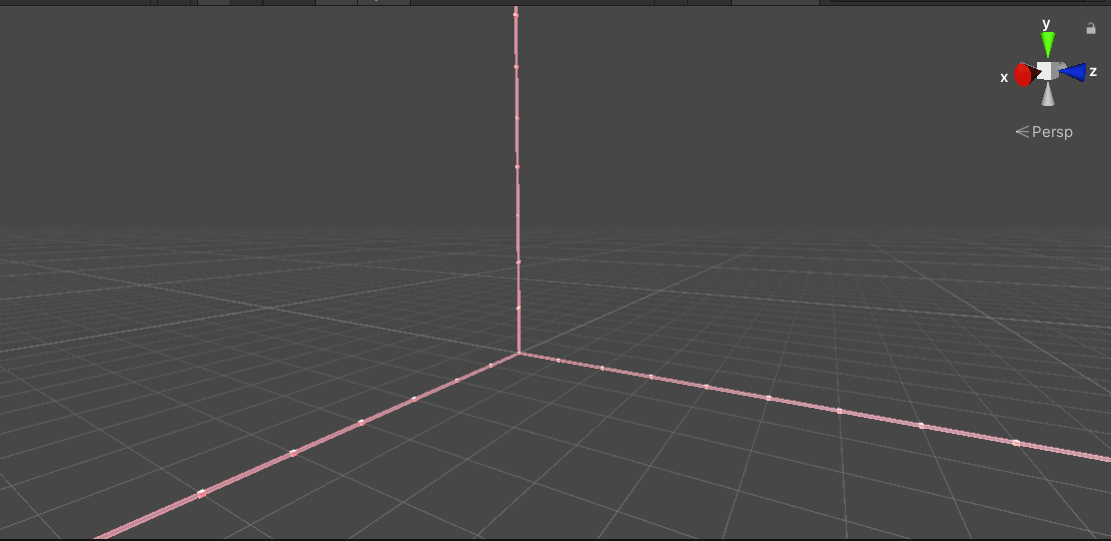
After a coordinate system is created, the basic points of Perlin Noise are selected by integer points on the X-axis and Y-axis of the coordinate system. In order to avoid overlapping with the coordinate system, the coordinate points of x=0 and z=0 are avoided
After the integer point is selected, the Y value can be obtained through the random function, so that the unique position can be determined in the three-dimensional coordinate system:
//Get the value of an integer point and instantiate an object at that position
void CreatePoints()
{
for (int i = 0; i < v2.x; i++)
{
for (int j = 0; j < v2.y; j++)
{
float nub = UnityEngine.Random.Range(0, MaxNoise);
GameObject go = Instantiate(itemPre, parent);
go.transform.position = new Vector3(i+1, nub, j+1);
items[i, j] = nub;
}
}
}
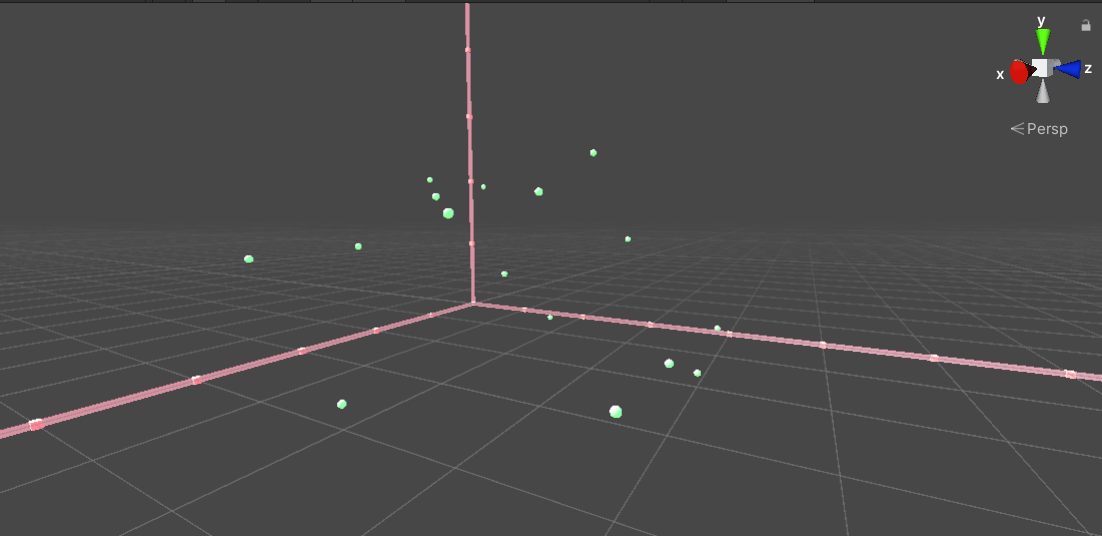
By executing the above code, the points corresponding to integer points can be generated in the scene. These points can be used as reference points and as cardinal points for subsequent interpolation operations:
Free angle:
Top view angle:
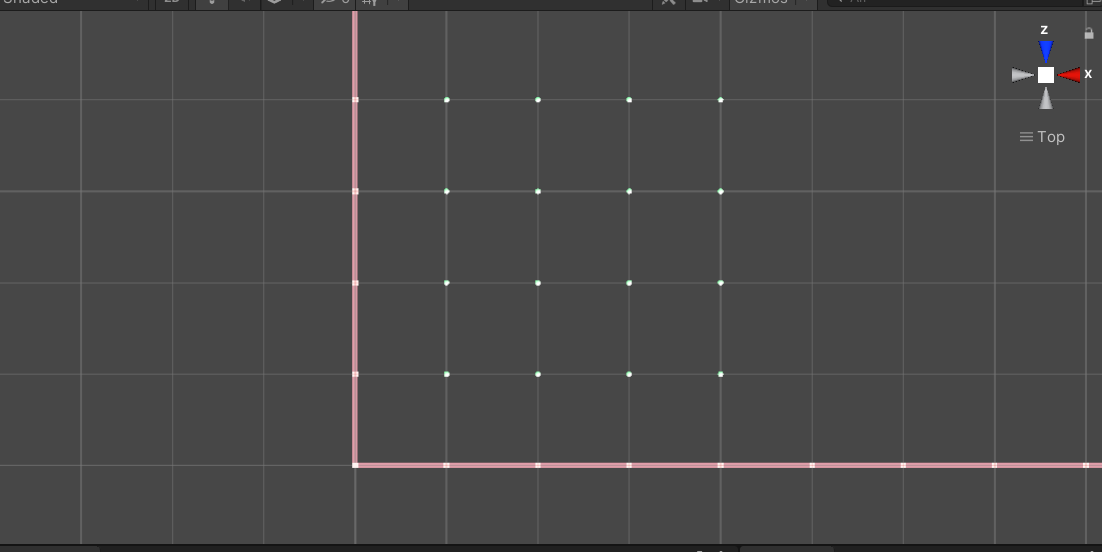
After completing the above preparations, we come to the focus of two-dimensional Perlin Noise, how to obtain the y value of non integer points through interpolation
Unlike one-dimensional Berlin noise, which only needs to perform one interpolation operation to obtain the corresponding number, two-dimensional Berlin noise needs to obtain the final result according to the numbers of the four nearest integer points around it, so we need to adopt some interpolation strategy to connect the four numbers
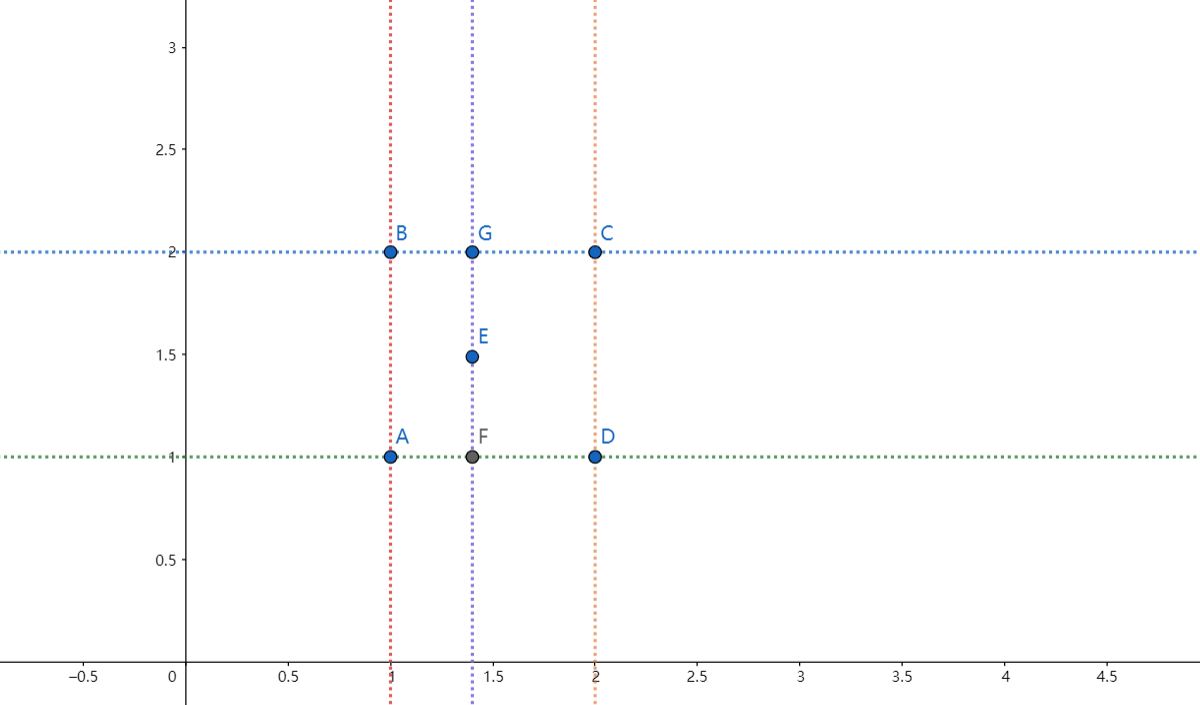
Similar to bilinear interpolation, Perlin Noise obtains the final result through cubic interpolation. It is introduced in the Wikipedia mentioned earlier:

In short, for A point in the rectangle composed of its nearest four coordinate points, as shown in the figure below, for point E, it needs to be interpolated according to the values of points A, B, C and D. the logic of interpolation is to first calculate the value of point F through the values of points A and D, and then calculate the value of point G through the values of points B and C, Finally, the final value is obtained through the value interpolation of G and F.
Compared with the calculation of intermediate value by one-dimensional Perlin Noise, two-dimensional Perlin Noise only performs two more interpolation operations, and the core code is simply changed:
//Calculate the interpolation of the points of the matrix composed of four adjacent integer points
public void CreateGrid(int x,int y)
{
for (int i = 0; i < 11; i++)
{
for (int j = 0; j < 11; j++)
{
float interX = Mathf.Lerp(items[x, y], items[x + 1, y], InterpolationCalculation1(i/10f));
float interY = Mathf.Lerp(items[x, y+1], items[x + 1,y+1], InterpolationCalculation1(i / 10f));
float inter = Mathf.Lerp(interX, interY, InterpolationCalculation1(j/ 10f));
GameObject go = Instantiate(itemPre, parent);
go.transform.position = new Vector3(x+ i /10f+1, inter, y+ j/10f+1);
}
}
}
//Calculation of interpolation function
float InterpolationCalculation1(float num)
{
return 6 * Mathf.Pow(num, 5) - 15 * Mathf.Pow(num, 4) + 10 * Mathf.Pow(num, 3);
}
By executing the code, you can see the visualization effect of two-dimensional Berlin noise:
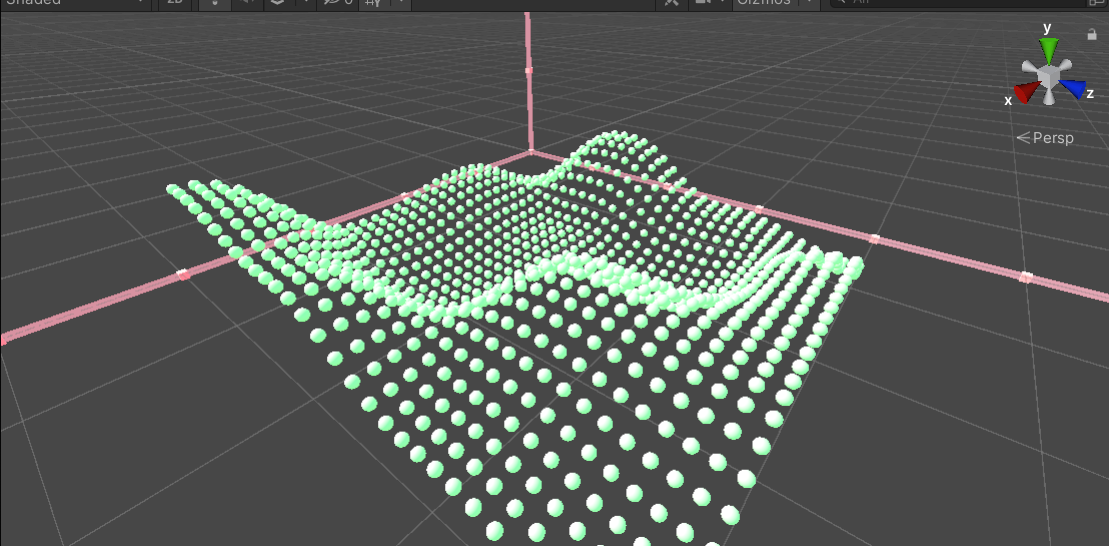
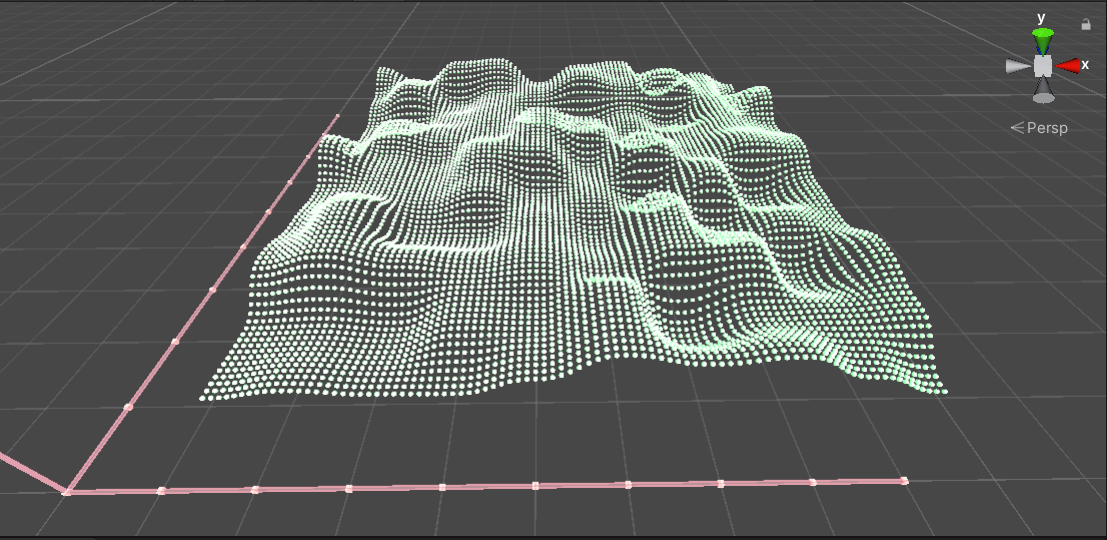
It can be seen from the above picture that the graphics created based on two-dimensional Perlin Noise are very close to the natural terrain, which is why they can be applied in terrain creation
Perfect Berlin noise
As mentioned earlier, Berlin noise is a pseudo-random algorithm. The terrain created each time should behave the same at the same coordinate point. However, in the above demonstration, the value of each integer point is generated by random function, that is, the terrain created each time is completely random
In the previous demonstration, the factors that completely randomly affect the terrain are only the values corresponding to integer points. If we have a method that can give the same value in a certain state, the final calculated terrain should also be the same. In order to avoid this problem, Perlin Noise proposed a solution, which can give the initial value of integer points:

Although the array has been given, it does not directly use the values in it, but is finally mapped to a group of gradients with a small range after conversion according to certain rules. The part about gradients is complex and difficult to understand. Therefore, it is not introduced above, but the deduction of simplified ideas. The whole specific algorithm ideas are introduced later, The whole process is very interesting. You can have a look if you are interested
Little knowledge
In my world, a unique terrain data can be obtained through a string of simple seed data. The logic at the bottom is similar to the preset value processing of Berlin noise
Algorithm idea of Berlin noise
In the above demonstration process, in order to avoid obscure mathematical knowledge, it is only handled at the application level. If you want to understand from theoretical knowledge, you can understand the whole process through the Java version of the source code given by Ken Perlin:
public final class ImprovedNoise
{
static public double noise(double x, double y, double z)
{
int X = (int)Math.floor(x) & 255, // FIND UNIT CUBE THAT
Y = (int)Math.floor(y) & 255, // CONTAINS POINT.
Z = (int)Math.floor(z) & 255;
x -= Math.floor(x); // FIND RELATIVE X,Y,Z
y -= Math.floor(y); // OF POINT IN CUBE.
z -= Math.floor(z);
double u = fade(x), // COMPUTE FADE CURVES
v = fade(y), // FOR EACH OF X,Y,Z.
w = fade(z);
int A = p[X] + Y, AA = p[A] + Z, AB = p[A + 1] + Z, // HASH COORDINATES OF
B = p[X + 1] + Y, BA = p[B] + Z, BB = p[B + 1] + Z; // THE 8 CUBE CORNERS,
return lerp(w, lerp(v, lerp(u, grad(p[AA], x, y, z), // AND ADD
grad(p[BA], x - 1, y, z)), // BLENDED
lerp(u, grad(p[AB], x, y - 1, z), // RESULTS
grad(p[BB], x - 1, y - 1, z))),// FROM 8
lerp(v, lerp(u, grad(p[AA + 1], x, y, z - 1), // CORNERS
grad(p[BA + 1], x - 1, y, z - 1)), // OF CUBE
lerp(u, grad(p[AB + 1], x, y - 1, z - 1),
grad(p[BB + 1], x - 1, y - 1, z - 1))));
}
static double fade(double t) { return t * t * t * (t * (t * 6 - 15) + 10); }
static double lerp(double t, double a, double b) { return a + t * (b - a); }
static double grad(int hash, double x, double y, double z)
{
int h = hash & 15; // CONVERT LO 4 BITS OF HASH CODE
double u = h < 8 ? x : y, // INTO 12 GRADIENT DIRECTIONS.
v = h < 4 ? y : h == 12 || h == 14 ? x : z;
return ((h & 1) == 0 ? u : -u) + ((h & 2) == 0 ? v : -v);
}
static final int p[] = new int[512], permutation[] = { 151,160,137,91,90,15,
131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23,
190, 6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
88,237,149,56,87,174,20,125,136,171,168, 68,175,74,165,71,134,139,48,27,166,
77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
102,143,54, 65,25,63,161, 1,216,80,73,209,76,132,187,208, 89,18,169,200,196,
135,130,116,188,159,86,164,100,109,198,173,186, 3,64,52,217,226,250,124,123,
5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
223,183,170,213,119,248,152, 2,44,154,163, 70,221,153,101,155,167, 43,172,9,
129,22,39,253, 19,98,108,110,79,113,224,232,178,185, 112,104,218,246,97,228,
251,34,242,193,238,210,144,12,191,179,162,241, 81,51,145,235,249,14,239,107,
49,192,214, 31,181,199,106,157,184, 84,204,176,115,121,50,45,127, 4,150,254,
138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180
};
static { for (int i=0; i< 256 ; i++) p[256 + i] = p[i] = permutation[i]; }
}
The whole process is similar to the above visual demonstration, but some knowledge is omitted in the understanding of the principle. It is added here to facilitate readers to learn and understand. Starting from the code, it is mainly divided into the following steps:
- Processing and conversion of coordinates
- Gets the hash value of an integer point based on the given array
- The gradient is obtained according to the hash value of the integer points around it
- Obtain the corresponding value of the current point through interpolation
Firstly, the processing of coordinate points is to obtain the coordinate values of the surrounding integer points according to the integer part of the currently transmitted coordinates, and the decimal places are used as the parameter values of interpolation and positioning in a basic unit:
int X = (int)Math.floor(x) & 255, // FIND UNIT CUBE THAT
Y = (int)Math.floor(y) & 255, // CONTAINS POINT.
Z = (int)Math.floor(z) & 255;
x -= Math.floor(x); // FIND RELATIVE X,Y,Z
y -= Math.floor(y); // OF POINT IN CUBE.
z -= Math.floor(z);
The above code obtains two sets of data through floor method (rounding down) and bit operation:
- (X, Y, Z): downward integer division 256 remainder, which is used to obtain the hash value of integer points later
- (x, y, z): subtract the rounding down itself, which is simply the mapping of the nearest square unit to 0 to 1
Here is a brief introduction to bit operation, which is essentially converted into binary for bit-to-bit operation. The bit operation of & used in Perlin Noise is essentially for remainder. Because it is an operation between bits, it has high operation efficiency. The specific binary calculation is as follows:
&The calculation rules of representation and operation are as follows:
1&1=1 1&0 =0 0&1 = 0 0&0 = 0
Therefore, in this operation, an integer x and 255 perform & operation. Assuming that the integer is 257, the calculation process is as follows:
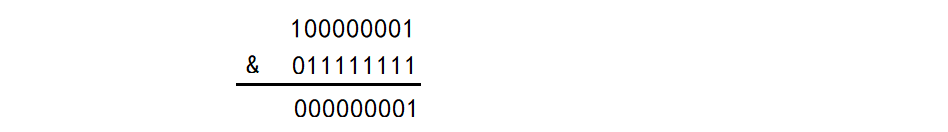
In the above process, the bits exceeding 255 are zeroed through the sum operation, while the bits less than or equal to 255 are equal to themselves after the sum operation, so as to achieve the effect of remainder
After that, we need to get the hash value calculated by integer points. The purpose of this step is to make a single arrangement for two-dimensional or higher dimensional coordinate points, so that the rectangular unit of coordinate points can correspond to the single array:
int A = p[X] + Y, AA = p[A] + Z, AB = p[A + 1] + Z, // HASH COORDINATES OF
B = p[X + 1] + Y, BA = p[B] + Z, BB = p[B + 1] + Z; // THE 8 CUBE CORNERS,
static final int p[] = new int[512], permutation[] = { 151,160,137,91,90,15,
131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23,
190, 6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
88,237,149,56,87,174,20,125,136,171,168, 68,175,74,165,71,134,139,48,27,166,
77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
102,143,54, 65,25,63,161, 1,216,80,73,209,76,132,187,208, 89,18,169,200,196,
135,130,116,188,159,86,164,100,109,198,173,186, 3,64,52,217,226,250,124,123,
5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
223,183,170,213,119,248,152, 2,44,154,163, 70,221,153,101,155,167, 43,172,9,
129,22,39,253, 19,98,108,110,79,113,224,232,178,185, 112,104,218,246,97,228,
251,34,242,193,238,210,144,12,191,179,162,241, 81,51,145,235,249,14,239,107,
49,192,214, 31,181,199,106,157,184, 84,204,176,115,121,50,45,127, 4,150,254,
138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180
};
static { for (int i=0; i< 256 ; i++) p[256 + i] = p[i] = permutation[i]; }
The four points in the three-dimensional case are listed in the code, and the latter four points are converted in the later calculation. Through the code, you can see that the array value corresponding to an integer point is hash converted through the three axes of the coordinates
Assuming that the coordinates of A coordinate point A are (x,y,z), the code structure of the data obtained from the array through hash conversion is:
int posA=p[p[p[x]+y]+z];
At the same time, because the values in the array are non repeating numbers from 0 to 255, if only subscript addition is carried out in this way, it will obviously cause the array to cross the boundary. So Ken Perlin chose to double the size of the array to avoid this problem
After getting the corresponding value from the array, you need to get the dot product of the gradient value corresponding to the integer point and the distance vector. In this process, you need to understand that the gradient vector corresponding to the integer point is not calculated, but selects the corresponding gradient from some given gradients based on the numbers previously obtained in the array
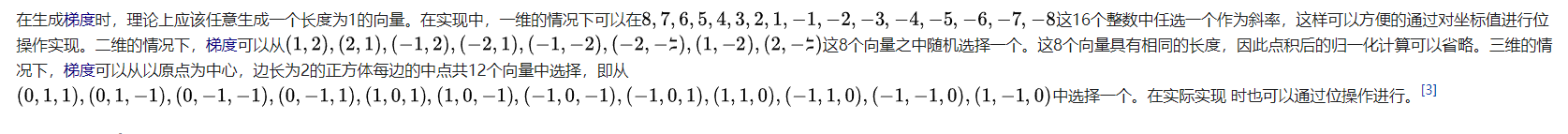
Then, how to find the corresponding unique gradient through a given number? Ken Perline uses the bit flip operation in the algorithm to obtain the final gradient. In the code case:
static double grad(int hash, double x, double y, double z)
{
int h = hash & 15; // CONVERT LO 4 BITS OF HASH CODE
double u = h < 8 ? x : y, // INTO 12 GRADIENT DIRECTIONS.
v = h < 4 ? y : h == 12 || h == 14 ? x : z;
return ((h & 1) == 0 ? u : -u) + ((h & 2) == 0 ? v : -v);
}
The weight of the integer point in the current gradient point is obtained by converting the value obtained by the previous hash conversion with the decimal coordinates of the point
In this part, there is a mathematical concept: gradient
The gradient represents the directional derivative of a function at the point, and the maximum value is obtained along the direction. In short, a two-dimensional function can be used to represent a surface in three-dimensional space. If y is specified as constant, a curve that changes with the change of x can be obtained. The function of this curve is the partial derivative of a two-dimensional function, and the slope of any point on this curve can be expressed by a vector, the direction represents positive and negative, and the length represents size. Based on this idea, the vector of the slope of the partial derivative relative to y at this point can also be calculated, and the sum of the two vectors is the gradient vector of this point:
For more details on gradient vectors, see this video: Click go
The last part is to interpolate the gradients of all integer points around the current point. The function used for interpolation is a continuous monotonic function with 1 at 0, 0 at 1 and 0.5 at 0.5. That's why it is selected 6 t 5 − 15 t 4 + 10 t 3 {\displaystyle 6t^{5}-15t^{4}+10t^{3}} 6t5 − 15t4+10t3 and 3 t 2 − 2 t 3 {\displaystyle 3t^{2}-2t^{3}} The reason why 3t2 − 2t3 is used as interpolation function is shown in the figure:
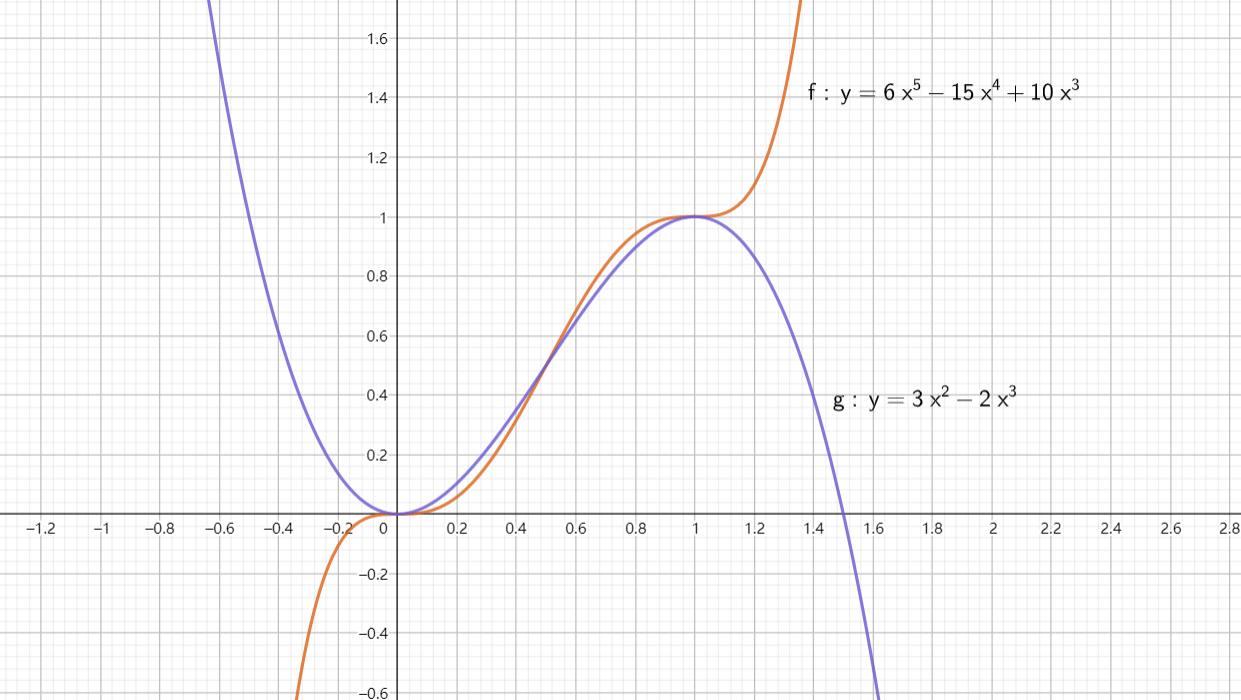
The two curves between 0 and 1 are basically the same, but 6 t 5 − 15 t 4 + 10 t 3 {\displaystyle 6t^{5}-15t^{4}+10t^{3}} 6t5 − 15t4+10t3 the curve is more gentle when approaching the end point