1, Basic concepts
let a0,a1,..., an all be numbers in the number field F, and n be nonnegative integers, then the expression anxn +an-1xn-1 +... + a2x2 +a1x1+ a0x0(an ≠ 0) is called the polynomial or univariate polynomial of the last character X in the number field F.
in polynomials, a0 is called zeroth order polynomial or constant term, a1x is called first order term, generally, aix is called i-order term, and ai is called the coefficient of i-order term. Univariate polynomials are represented by the symbols f(x), g(x).
univariate sparse polynomial: in univariate polynomials, if the number of terms with a coefficient of 0 (i.e. nonexistent terms, referring to terms lower than the highest order) is far more than the number of non-0 terms (existing terms), and the distribution of non-0 terms is irregular, the univariate polynomial is called univariate sparse polynomials.
2, Problem description
- The output polynomial is in the form of integer sequence: n,a1,e1,a2,e2,..., an,en, where n is the number of terms of the polynomial, AI and EI are the coefficients and exponents of the i-th term respectively, and the sequence is arranged in exponential descending order.
- Realize the addition of polynomials a and b.
- Realize the subtraction of polynomials a and b.
- Realize the multiplication of polynomials a and b.
Input example:
7-5x2+9x5— >3 7 0 -5 2 9 5
Test case:
(x + x2) + 0 = x + x2
(x + x2) - (x + x2) = 0
0 + 0 = 0
(x + x2) + (-x + 5x5) = x2 + 5x5
3, Polynomial storage
univariate sparse polynomials have high storage efficiency with linked lists.
typedef struct Polynomial{//term
float coef;//coefficient
int expn;//index
struct Polynomial *next;//Pointer, next item
}Polynomial;
the linked list in the program has a head node, which can facilitate the operation of the linked list.
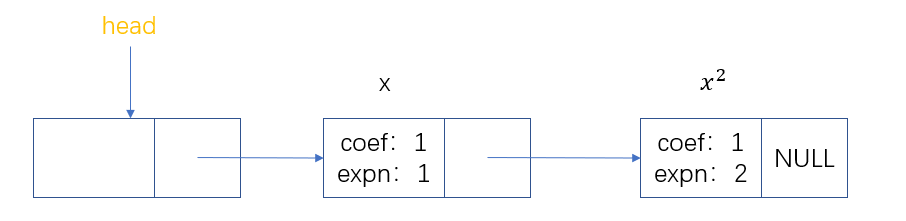
take the storage of polynomial x + x2 as an example. As shown below:
Univariate sparse polynomial linked list construction code:
void createPolynomial(Polynomial *head){
printf("Please enter the number of items:");
int n;
scanf("%d",&n);//Get number of items
for(int i=1;i<=n;i++){
Polynomial *p = (Polynomial *)malloc(sizeof(Polynomial));
printf("Please enter page%d Coefficients and indices of:",i);
scanf("%f %d",&p->coef,&p->expn);
if(p->coef == 0)//The coefficient is 0 and is not stored
free(p);
else{
Polynomial *p1, *p2;//Two pointers, one in front and one behind, are convenient for operation
p1 = head;
p2 = head->next;
while(p2 != NULL && p2->expn < p->expn){//Found / or empty with index greater than p
p1 = p2;
p2 = p2->next;
}
if(p2 != NULL && p2->expn == p->expn){//Index equality, consolidation
p2->coef += p->coef;
if(p2->coef == 0){//If the combined coefficient is 0, this item will be deleted
p1->next = p2->next;
free(p2);
}
free(p);
}
else{//If there is no exponential equality, it is added after p1
p->next = p2;
p1->next = p;
}
}
}
}
4, Polynomial addition and subtraction method
Basic idea: all polynomials are exponentially sorted, so we can operate like the merging of monotonic linked lists.
- When the exponents are equal, the coefficients are added (subtracted when subtracting); if the added coefficients are not 0, they are saved in linked list C;
- If the indexes are not equal, if the index of A is less than that of B, save the coefficients and indexes in the node of A into the linked list C;
- On the contrary, the coefficients and indexes in the node of B are stored in the linked list C;
- When there are more items in a linked list, they are also saved in linked list C.
Polynomial addition and subtraction code implementation: index control addition and subtraction, 1 is addition, - 1 is subtraction; A+B or A-B; Return result linked list
Polynomial* addPolynomial(Polynomial *headA, Polynomial *headB,int index){//Head A: polynomial A; headB: polynomial B; index: addition and subtraction mark, addition 1, subtraction-1
Polynomial *headC = (Polynomial *)malloc(sizeof(Polynomial));//Create polynomial c
headC->next = NULL;
Polynomial *a1 = headA, *a2 = headA->next;//Polynomial A sets two flags
Polynomial *b1 = headB, *b2 = headB->next;//Polynomial B sets two flags
Polynomial *c1 = headC;//Tail marking of polynomial C
while(a2 && b2){//Cyclic comparison, put the one with small index in front
if(a2->expn < b2->expn){//If the exponent of a2 is less than b2, put a2 into the tail of c
a1->next = a2->next;//Separate a2 from a
a2->next = c1->next;
c1->next = a2;//Connect a2 to the tail of c
a2 = a1->next;//a2 points to the last node of a1
c1 = c1->next;//Move c1 to the tail of c (move one back because you just added one)
}
else if(a2->expn == b2->expn){//a2 and b2 have the same index. They are combined and put into the tail of c
a2->coef += index * b2->coef;//The addition and subtraction method can be controlled by setting index
if(a2->coef != 0){//The combined coefficient is not 0, so it is necessary to add the combined a2 to c
a1->next = a2->next;//Separate a2 from a
a2->next = c1->next;
c1->next = a2;//Connect a2 to the tail of c
c1 = c1->next;//Move c1 to the tail of c (move one back because you just added one)
a2 = a1->next;//a2 points to the last node of a1
b1->next = b2->next;//Separate b2, too
free(b2);//Free up space for b2
b2 = b1->next;//b2 points to the next node of b1
}
else{//If the combined coefficient is 0, it does not need to be added to c
a1->next = a2->next;//Remove a2
free(a2);//Free a2 space
a2 = a1->next;
b1->next = b2->next;//Remove b2
free(b2);//Free b2 space
b2 = b1->next;
}
}
else{//If the exponent of b2 is less than a2, put b2 into the tail of c
b1->next = b2->next;//Separate b2 from b
b2->next = c1->next;
c1->next = b2;//Connect b2 to the tail of c
b2 = b1->next;//b2 points to the next node of b1
c1 = c1->next;//Move c1 to the tail of c (move one back because you just added one)
}
}
while(a2){
a2->coef *= index;//Minus, let the coefficient change sign
a1->next = a2->next;//Connect a2 after c
a2->next = c1->next;
c1->next = a2;
c1 = c1->next;
a2 = a1->next;
}
while(b2){
b2->coef *= index;//Minus, let the coefficient change sign
b1->next = b2->next;//Connect b2 after c
b2->next = c1->next;
c1->next = b2;
c1 = c1->next;
b2 = b1->next;
}
return headC;//Return polynomial c
}
5, Polynomial multiplication
Basic idea: multiply by bit, loop traversal; Time complexity n2;
A = a1xi1+a2xi2
B = b1xi3+b2xi4
A * B = a1*b1xi1+i3 + a1*b2xi1+i4 + a2*b1xi2+i3 + a2*b2xi2+i4
Polynomial* multiplyPolynomial(Polynomial *headA, Polynomial *headB){//A times B
Polynomial *headC = (Polynomial *)malloc(sizeof(Polynomial));//Create polynomial c
headC->next = NULL;
Polynomial *a1 = headA, *a2 = headA->next;//Polynomial A sets two flags
Polynomial *b1 = headB, *b2 = headB->next;//Polynomial B sets two flags
Polynomial *c1 = headC;//Tail marking of polynomial C
while(a2){
b2 = headB->next;
while(b2){
Polynomial *p = (Polynomial *)malloc(sizeof(Polynomial));
p->coef = a2->coef * b2->coef;//Coefficient difference
p->expn = a2->expn + b2->expn;//Exponential addition
if(p->coef == 0)//The coefficient is 0 and is not stored
free(p);
else{
Polynomial *p1, *p2;//Two pointers, one in front and one behind, are convenient for operation
p1 = c1;
p2 = c1->next;
while(p2 != NULL && p2->expn < p->expn){//Found / or empty with index greater than p
p1 = p2;
p2 = p2->next;
}
if(p2 != NULL && p2->expn == p->expn){//Index equality, consolidation
p2->coef += p->coef;
if(p2->coef == 0){//If the combined coefficient is 0, this item will be deleted
p1->next = p2->next;
free(p2);
}
free(p);
}
else{//If there is no exponential equality, it is added after p1
p->next = p2;
p1->next = p;
}
}
b2 = b2->next;//b2 move down one
}
a2 = a2->next;//a2 move down one
}
return headC;//Return polynomial c
}