2. Save xiaoha

Task:

The maze consists of n rows and m columns of cells (n and m are less than or equal to 50), and each cell is either an open space or an obstacle.

The task is to help Xiao hum find the shortest path from the beginning of the maze to Xiao ha's location. Pay attention to the obstacles. Of course, Xiao hum can't go out of the maze.

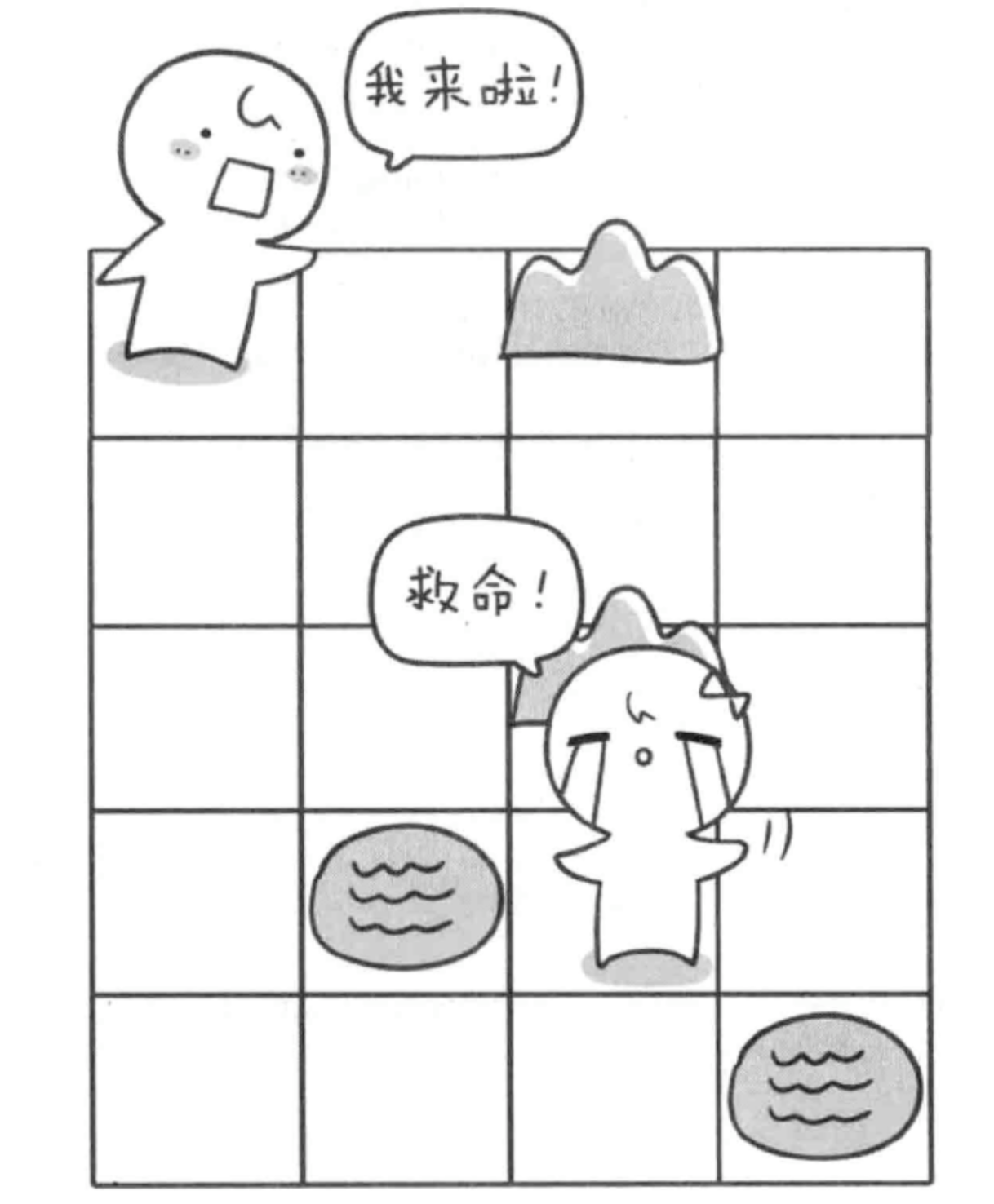
answer:

First, you can use a two-dimensional array to store the maze.

You can only try one by one. You can let Xiao hum go to the right first, and then come back here when he can't get through, and then try another direction.

Here, a sequence is specified. Try in a clockwise direction (that is, try in the order of right, bottom, left and top).

For example, the following figure is a feasible search path:

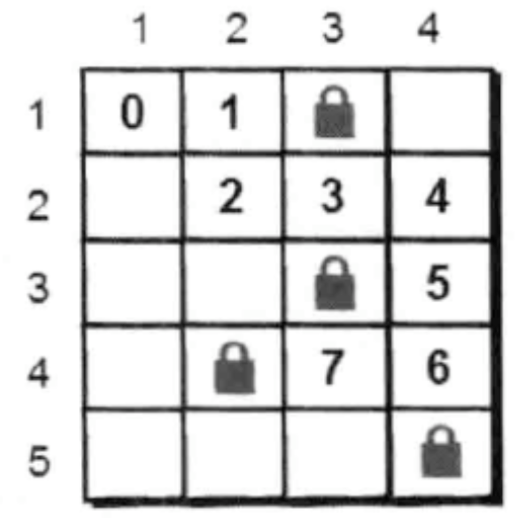
Now try to implement this method with depth first search.

Let's first look at how the dfs() function is written. The function of dfs() is to solve what should be done at present. What xiaohum needs to deal with when he is at a certain point is to check whether xiaohum has arrived
Reach xiaoha's position. If you don't arrive, find out where you can go next.

In order to solve this problem, the dfs() function only needs to maintain three parameters, namely, the x coordinate, y coordinate of the current point and the number of steps that have been taken step.

The dfs() function is defined as follows:

void dfs(int x, int y, int step) {
	return 0;
}

To judge whether xiaoha's position has been reached, you only need to judge whether the current coordinates are equal to xiaoha's coordinates. If they are equal, it indicates that xiaoha's position has been reached, as follows:

void dfs(int x, int y, int step) {
	if (x==p && y==q) {
		if (step < min) {
			min = step;
		}
		return;
	}
	return 0;
}

If you don't reach xiaoha's position, find out where you can go next.

Because there are four directions to go, try clockwise according to the previous agreement (that is, try in the order of right, bottom, left and top).

A direction array next is defined here, as follows:

int next[4][2] = {{0, 1},
					{1, 0},
					{0, -1},
					{-1, 0}};

for (k=0; k<=3; k++) {
	tx = x+next[k][0];
	ty = y+next[k][0];
}

Through this direction array, it is easy to obtain the coordinates of the next step by using the loop.

Here, the abscissa of the next step is stored in tx and the ordinate is stored in ty:

for (k=0; k<=3; k++) {
	tx = x+next[k][0];
	ty = y+next[k][1];
}

Next, we will make some judgment on the next point (tx, ty). Including whether it is out of bounds, whether it is an obstacle, and whether the point is already in the path (i.e. avoid repeated access to a point).

You need to use book[tx][ty] to record whether the grid (tx, ty) is already in the path.

If this point meets all requirements, the next step is to expand this point, that is, dfs(tx, ty, step+1):

for (k=0; k<=3; k++) {
	tx = x + next[k][x];
	ty = y + next[k][y];

	if (tx<1 || tx>n || ty<1 || ty>m) {
		if (a[tx][ty]==0 && book[tx][ty]==0) {
			book[tx][ty] = 1;
			dfs(tx,ty,step+1);
			book[tx][ty] = 0'
		}
	}
}

The complete code is as follows:

#include <stdio.h>

int n, m, p, q, min=99999999;
int a[51][51], book[51][51];

void dfs(int x, int y, int step) {
	int next[4][2] = {{0,1}, //turn right
						{1,0},//Go down 
						{0,-1}, //turn left
						{-1,0}};//Go up

	int tx, ty, k;
	//Judge whether to reach xiaoha's position
	if (x==p && y==q) {
		//Update minimum
		if (step<min) {
			min = step;
		}
		return;//Attention return
	}
	
	//Enumerate 4 ways
	for (k=0; k<=3; k++) {
		//Calculate the coordinates of the next point
		tx = x + next[k][0];
		ty = y + next[k][1];
		//Judge whether it is out of bounds
		if (tx<1 || tx>n || ty<1 || ty>n) {
			continue;
		}
		//Judge whether the point is an obstacle or is already in the path
		if (a[tx][ty]==0 && book[tx][ty]==0) {
			book[tx][ty] = 1;//Mark that this point has passed
			dfs(tx, ty, step+1);//Start trying the next point
			book[tx][ty] = 0;//At the end of the attempt, unmark this point
		}
	}
	return;
}


int main() {
	int i, j, startx, starty;
	//Read in N and m, where n is the row and M is the column
	scanf("%d %d", &n, &m);
	//Read into maze
	for (i=1; i<=n; i++) {
		for (j=1; j<=m; j++) {
			scanf("%d", &a[i][j]);
		}
	}
	//Read in start and end coordinates
	scanf("%d %d %d %d", &startx, &starty, &p, &q);
	//Search from start
	book[startx][starty] = 1;//The marked starting point is already in the path. Repeat after the method
	//The first parameter is the x coordinate of the starting point, the second parameter is the y coordinate of the starting point, and the third parameter is the initial steps 0
	dfs(startx, starty, 0);

	//Output minimum steps
	printf("%d", min);
	getchar();getchar();
	return 0;
}