1 . concept

1.1 true and pseudo-random numbers

Most computer languages provide API s for generating random numbers, which are called random number generators.

Computers can use random numbers to simulate various random probability problems in the real world. The programming language without random generator is not a "good language".

What is a true random number?

Random numbers in the real world: such as coin tossing, dice, runner, noise using electronic components, nuclear fission, etc.

The computer simulates the random number generated by this physical phenomenon in the real world through hardware technology. We call it true random number. Such random number generators are called physical random number generators. Generating true random number requires high hardware technology of computer.

**Characteristics of real random numbers: * * unpredictable.

For example, when you flip a coin, you can't really predict the face of the next coin.

What is a pseudo-random number?

The random number generated by algorithm simulation is called pseudo-random number. The random numbers generated in computer programming language are basically pseudo-random numbers.

**Characteristics of pseudo-random number: * * since it is simulated by the algorithm, although it is unpredictable in a short period, the random number in a long period is predictable.

1.2 random number seed

When generating pseudo-random numbers, you need to set random seeds. The role of seeds is to inject a dynamic variable into the generation algorithm of random numbers.

For example, using the current time of the system as a random seed, the random algorithm can generate a random number with greater randomness on the basis of time change. However, if random numbers are not generated at the millisecond level, a large number of random numbers generated at the same point in time may be equal.

When selecting seeds, you can consider synthesizing multi-dimensional change values for operation. For example, in UNIX system, the system time, WIFI connection, and even the number of keyboard presses are quantified as seed.

The more reference indexes, the closer the pseudo-random number is to the real random generation.

2. Python random module

Random module implements pseudo-random number generators of various distributions. Because of complete certainty, it is not suitable for all purposes, and it is not suitable for encryption purposes at all. The pseudo-random generator of this module should not be used for security purposes. For security or encryption purposes, you can use the secrets module in Python.

This makes it necessary to import the random module before

import random

2.1 method of random module

1. Initialize random seed

random.seed(a=None, version=2)

• If a is omitted or None, the current system time is used as a random seed.

• If the operating system provides random sources, use them instead of system time.

• If a is of type int, it is used directly.

  When the random seed is set to be a constant, the random number is fixed every time.

  import random
  #Setting random seed is an int constant
  random.seed(10)
  print(random.random())
  #Setting random seed is an int constant
  random.seed(10)
  print(random.random())
  #Setting random seed is an int constant
  random.seed(10)
  print(random.random())
  

  Output result:

  0.5714025946899135
  0.5714025946899135
  0.5714025946899135
  

1. Generate random numbers from a range of numbers

 random.randrange(start, stop[, step])

Returns a randomly selected element from range(start, stop, step).

This is equivalent to choice(range(start, stop, step)), but actually does not build a range object.

1. Returns a random integer

   random.randint(a, b)

Equivalent to randange (a, B + 1)

Result N meets: a < = N < = b

1. Returns a random element from the non empty sequence seq. If SEQ is empty, an IndexError exception is thrown.

random.choice(seq)

import random

lst = [5, 3, 90, 12, 4, 6]
r = random.choice(lst)
print(r)

Each run gets a random number from the list.

1. Randomly disrupt the sequence x

andom.shuffle(x[, random])

The optional parameter random is a parameterless function that returns random floating-point numbers in [0.0, 1.0); by default, this is the function random()

import random

lst = [5.0, 3.0, 90.0, 12.0, 4.0, 6.0]
#Use random Random function
random.shuffle(lst, random.random)
print(lst)
#Output results
[3.0, 90.0, 6.0, 12.0, 5.0, 4.0]
#----------------------------------
def my_random():
    return float(random.randint(0, 1))

lst = [5.0, 3.0, 90.0, 12.0, 4.0, 6.0]
#Use user defined functions
random.shuffle(lst, my_random)
print(lst)

1. Returns a list of k lengths of unique elements selected from an overall sequence or collection. For random sampling without repetition.

random.sample(population, k, *, counts=None)

1. Returns the next random floating-point number within the range of [0.0, 1.0].

random.random()

1. Returns a random floating-point number N

random.uniform(a, b)

Depending on the floating-point rounding in equation a + (b-a) * random(), the end point b may or may not be included in this range.

The result N satisfies: when a < = B, a < = N < = B, when B < A, B < = N < = a.

More methods can be found in the official documents.

3. Unpredictable beauty

3.1 random color dots

Problem solving idea: it can be drawn in combination with the turtle module, and the position of the random little turtle can be

import random
import turtle

colors = ["red", "blue", "green", "gray", "orange"]
for i in range(100):
    turtle.penup()
    x = random.randint(-300, 300)
    y = random.randint(-300, 300)

    turtle.goto(x, y)
    turtle.pendown()
    turtle.dot(20, colors[i % 5])

turtle.done()

3.2 find the value of π

Probability method, also known as Monte Carlo method, is a very important numerical calculation method.

This method is a calculation method based on probability and statistical theory. The problem solved is connected with a certain probability model, and the computer is used to realize statistical simulation or sampling, so as to obtain the approximate solution of the problem.

Suppose there is a circle with a radius of 1, as shown in the figure, the area of the shaded part (1 / 4 circle) in the figure is equal to 1 / 4 of the value. The approximate value of π is obtained by multiplying the shadow area of π by 1 / 4.

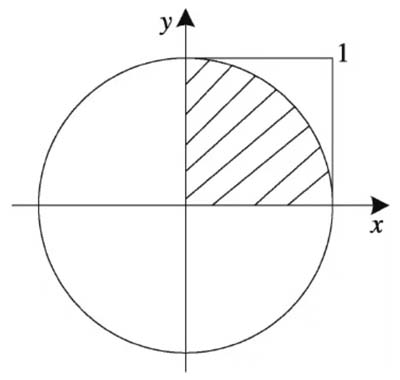
Solution idea

• The value x of abscissa and the value y of ordinate are generated by random function (both values should be 0 ~ 1)

• Judge whether the point composed of these two random numbers is located in the area of 1 / 4 circle (shaded part). If the point is located in the shaded area, count it.

• New points are generated continuously. Because the point coordinates generated by the random function have a certain uniformity, when there are enough points, the approximate uniform distribution of points inside and outside the shadow can be obtained.

• Finally, divide the number of points in the shadow by the total number of points to obtain the approximate shadow area, which is an approximate value of 1 / 4.

  import random
  
  i, n, s = 0, 0, 0
  x, y = 0.0, 0.0
  n = int(input("Enter the number of points:"))
  random.seed()
  for i in range(n):
      x = random.random()
      y = random.random()
      if (x * x + y * y) <= 1:
          s += 1
  
print("PI=%f\n", 4 * s / n)

Output result:

Number of input points: 9000000
PI= 3.141477777777778

The more points you enter, the more accurate the approximate value of PI will be.

4 . summary

Random numbers can perfectly simulate various probabilities or random events in the real world. In addition to the random module, the random number generation of python can also use the methods provided in the numpy library.