USACO4.3.2--Violent Solution to Prime Matrix
Topic link: Here;
After reading the questions, it is not difficult to find that this is a completed number of questions. First, say the filling method. Most people must think of one line at the beginning, one column at the beginning, and then judge as a whole after filling out the questions. Big data just wastes you T: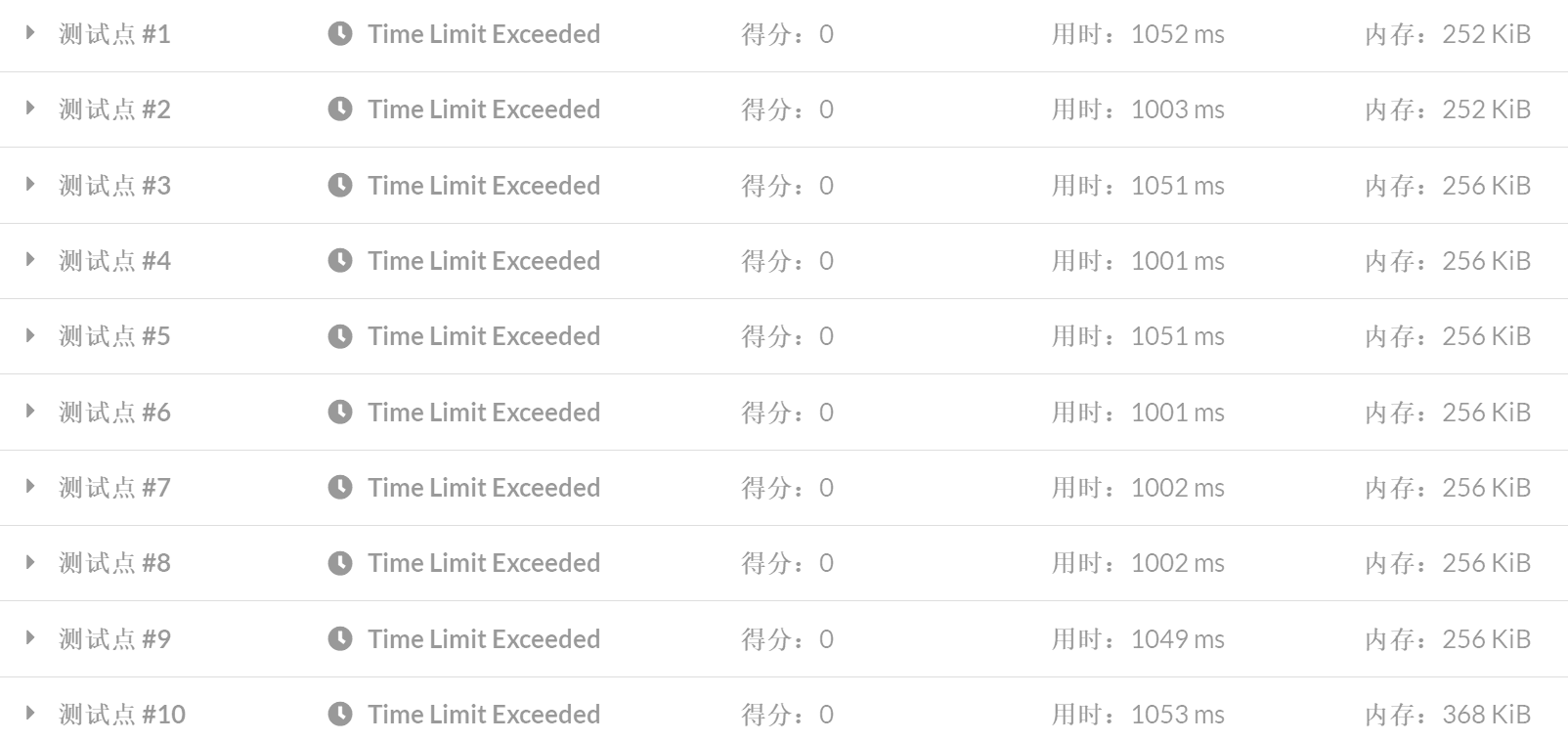
So we start to focus on some of the identified points. The more identified the points, the fewer prime numbers to choose from and the faster they run. See the following figure:
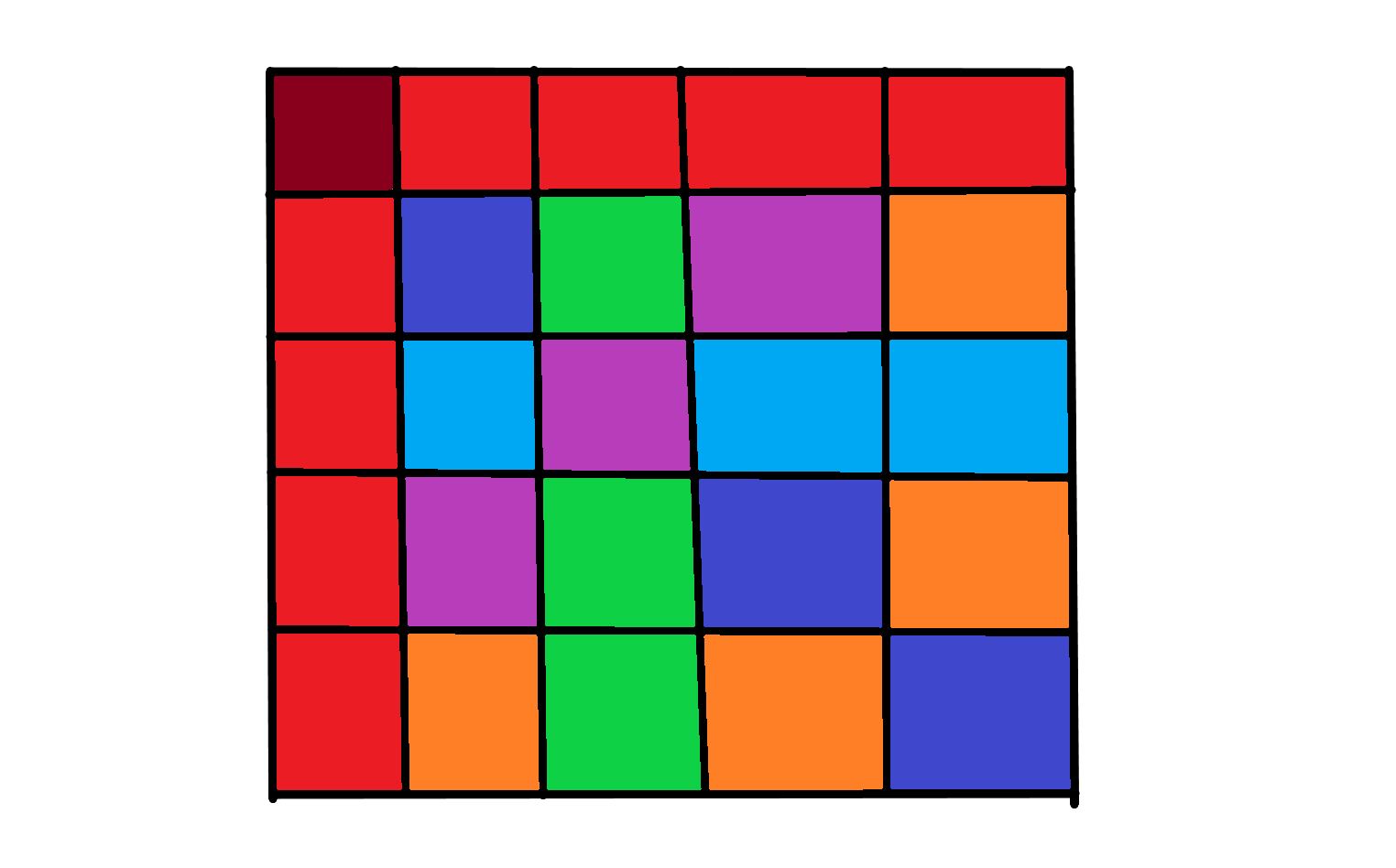
The dark red (top left corner) in the picture indicates the point identified in the title. First we fill in the first row, the first column (red), so there is a constraint (one end is OK), then the top right-bottom slant (purple), so there are two constraints (one end is OK), then the top left-bottom right slant (dark blue), then the light blue and green, and they areThere are two constraints.Finalize the orange value, subtract the other four numbers from the total value, and return to do it again if it is negative or greater than 10.
After the whole is done, judge according to the conditions given by the title, and return to do it again if it does not meet the requirements.
Answers need to be sorted before they can be output, and a two-dimensional array of answers is stored in a string for easy comparison.
The key point to mention here is judgment. Here is a piece of code that I just started writing:
bool Judge_Num(int Num) {
for (register int i = 2; i <= sqrt(Num); i++)
if (Num % i == 0)
return false;
// cout<<Num<<endl;
return true;
}
Note that it explodes - it takes a lot of time to compute sqrt once per loop, so I made the following improvements:
bool Judge_Num(int Num) {
int T=sqrt(Num);//So just calculate sqrt once
for (register int i = 2; i <= T; i++)
if (Num % i == 0)
return false;
// cout<<Num<<endl;
return true;
}
But it will still time out (Num is a five-digit number, less than 100 times per cycle), can you reduce the time to O(1)?
Tolerable:
Before filling in the number, we use Euler sieve to sift out the prime numbers from 10000 to 99999, store them with bool array Visited, Visited[N]=1 means N is prime, Visited[N]=0 means N is not prime, so we only need to:
bool Judge_Num(int Num){
return true-Visited[Num];
}
Everything will be fine
Code (the longest in USACO history):
#include "bits/stdc++.h"
using namespace std;
struct Unsigned {
int Size, Num[1001];
int E[1001][11];
} Prime[11];//Store each prime number
int Sum, Start, Used[9], Result[9][9], Size, prime[100100];
bool Can, Visited[100101];
const int N = 5, M = 9;
struct Out {
string Name;
int Num_Result[9][9];
friend bool operator<(Out Num1, Out Num2) { return Num1.Name < Num2.Name; }
} HaHaHa[999];
//Sort of answers
void Made_Prime(void) {
for (int i = 2; i <= 100100; i++) {
if (!Visited[i])
prime[++prime[0]] = i;
for (int j = 1; j <= prime[0] && i * prime[j] <= 100100; j++) {
Visited[i * prime[j]] = 1;
if (i % prime[j] == 0)
break;
}
}
return;
}//Euler sieve
bool Judge_Num(int Num) {
return true - Visited[Num];
}//Qualification
void DFS_Made(int K, int Last, int Already) {
if (Last > 9 * (N - K))
return;
if (K == N) {
if (Last == 0 && Judge_Num(Already) == true) {
int JJ = Already, KK = N;
++Prime[Already / 10000].Size;
int UU = Prime[Already / 10000].Size;
Prime[Already / 10000].Num[UU] = Already;
while (JJ != 0) {
Prime[Already / 10000].E[UU][KK] = JJ % 10;
KK--, JJ = JJ / 10;
}
}
return;
}
for (register int i = 0; i <= 9; i++) DFS_Made(K + 1, Last - i, Already * 10 + i);
return;
}//Integrate legal five-digit prime numbers
bool Judge(void) {
int Sum_Judge = 0, Mul_Judge = 0;
for (register int i = 1; i <= N; i++) {
Sum_Judge = 0;
for (register int j = 1; j <= N; j++) Sum_Judge = Sum_Judge + Result[j][i];
if (Sum_Judge != Sum)
return false;
}
for (register int i = 1; i <= N; i++) {
Mul_Judge = 0;
for (register int j = 1; j <= N; j++) Mul_Judge = Mul_Judge * 10 + Result[j][i];
if (Judge_Num(Mul_Judge) == false)
return false;
}
for (register int i = 1; i <= N; i++) {
Sum_Judge = 0;
for (register int j = 1; j <= N; j++) Sum_Judge = Sum_Judge + Result[i][j];
if (Sum_Judge != Sum)
return false;
}
for (register int i = 1; i <= N; i++) {
Mul_Judge = 0;
for (register int j = 1; j <= N; j++) Mul_Judge = Mul_Judge * 10 + Result[i][j];
if (Judge_Num(Mul_Judge) == false)
return false;
}
Sum_Judge = 0, Mul_Judge = 0;
for (register int i = 1; i <= N; i++) {
Mul_Judge = Mul_Judge * 10 + Result[i][i];
Sum_Judge = Sum_Judge + Result[i][i];
}
if (Sum_Judge != Sum || Judge_Num(Mul_Judge) == false)
return false;
Sum_Judge = 0, Mul_Judge = 0;
for (register int i = 1; i <= N; i++) {
Mul_Judge = Mul_Judge * 10 + Result[N - i + 1][i];
Sum_Judge = Sum_Judge + Result[N - i + 1][i];
}
if (Sum_Judge != Sum || Judge_Num(Mul_Judge) == false)
return false;
return true;
}
bool Judge_Zero(int *QQ) {
for (register int i = 1; i <= N; i++)
if (QQ[i] == 0)
return false;
return true;
}//Judging the validity of a matrix
int main(void) {
cin >> Sum >> Start;
if (Sum < Start + 4 || Sum % 3 == 0) {
cout << "NONE" << endl;
return 0;
}//If the sum is too small or every five digits is a multiple of three, there is no solution.
Made_Prime();
for (register int i = 1; i <= 9; i++) DFS_Made(1, Sum - i, i);
//Integrate prime numbers
//The following code is longer, actually filling in the grid
for (register int ii = 1; ii <= Prime[Start].Size; ii++) {
if (Judge_Zero(Prime[Start].E[ii]) == true) {
for (register int i = 1; i <= N; i++) Result[1][i] = Prime[Start].E[ii][i];
for (register int iii = 1; iii <= Prime[Start].Size; iii++) {
if (Judge_Zero(Prime[Start].E[iii]) == true) {
for (register int i = 1; i <= N; i++) Result[i][1] = Prime[Start].E[iii][i];
int T = Result[N][1];
for (register int i = 1; i <= Prime[T].Size; i++) {
if (Prime[T].E[i][N] == Result[1][N]) {
for (register int j = 1; j <= N; j++) Result[N - j + 1][j] = Prime[T].E[i][j];
int Y = Result[3][1];
for (register int j = 1; j <= Prime[Y].Size; j++) {
if (Prime[Y].E[j][3] == Result[3][3]) {
for (register int k = 1; k <= N; k++) Result[3][k] = Prime[Y].E[j][k];
int D = Result[1][1];
for (register int k = 1; k <= Prime[D].Size; k++) {
if (Prime[D].E[k][3] == Result[3][3]) {
for (register int l = 1; l <= N; l++)
Result[l][l] = Prime[D].E[k][l];
Result[N][2] = Sum - Result[1][2] - Result[2][2] - Result[3][2] -
Result[4][2];
if (Result[N][2] < 0 || Result[N][2] > 9)
continue;
int JJJJJJJ = 0, KKKKKKK = 1;
while (KKKKKKK <= N) {
JJJJJJJ = JJJJJJJ * 10 + Result[KKKKKKK][2];
KKKKKKK++;
}
if (Judge_Num(JJJJJJJ) == false)
continue;
//A small branch half filled
int G = Result[1][3];
for (register int l = 1; l <= Prime[G].Size; l++) {
if (Prime[G].E[l][3] == Result[3][3]) {
for (register int h = 1; h <= N; h++)
Result[h][3] = Prime[G].E[l][h];
Result[2][N] = Sum - Result[2][1] - Result[2][2] -
Result[2][3] - Result[2][4];
Result[4][N] = Sum - Result[4][1] - Result[4][2] -
Result[4][3] - Result[4][4];
Result[N][2] = Sum - Result[1][2] - Result[2][2] -
Result[3][2] - Result[4][2];
Result[N][4] = Sum - Result[1][4] - Result[2][4] -
Result[3][4] - Result[4][4];
if (Result[2][N] < 0 || Result[4][N] < 0 ||
Result[N][2] < 0 || Result[N][4] < 0)
continue;
if (Result[2][N] > 9 || Result[4][N] > 9 ||
Result[N][2] > 9 || Result[N][4] > 9)
continue;
//Judgment of Legality
if (Judge() == true) {
Can = true;
Size++;
for (register int iiii = 1; iiii <= N; iiii++) {
for (register int jj = 1; jj <= N; jj++) {
HaHaHa[Size].Num_Result[iiii][jj] =
Result[iiii][jj];
HaHaHa[Size].Name += ('0' + Result[iiii][jj]);
} // cout<<endl;
} // cout<<endl;
}
}
}
}
}
}
}
}
}
}
}
}
}
if (Can == false) {
cout << "NONE" << endl;
} else {
sort(HaHaHa + 1, HaHaHa + 1 + Size);
for (register int k = 1; k <= Size; k++) {
for (register int i = 1; i <= N; i++) {
for (register int j = 1; j <= N; j++) {
cout << HaHaHa[k].Num_Result[i][j];
}//Sort and output
cout << endl;
}
cout << endl;
}
}
return 0;
}

