1, Overview of parallel search set

1. Related concepts

(1) Introduction of union search set

problem

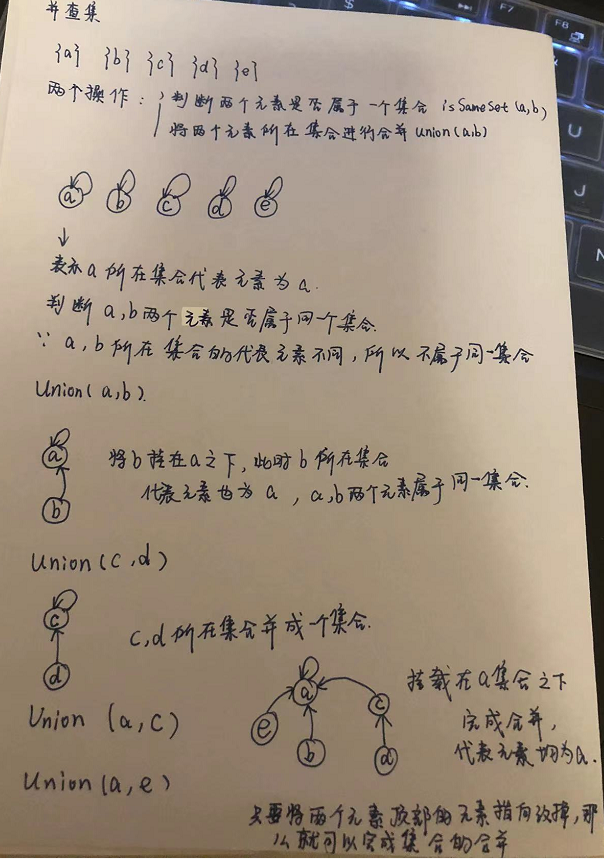
There are several sets, {a},{b},{c},{d},{e}
Design two methods

1. Judge whether two elements are in the same set, issameset(a, b)
2. Merge the set of elements a and B into union(a, b)

Solution

Identify a representative element for each collection and point up to an element
To judge whether two elements are in the same set is to judge whether the representative elements of the set where the two elements are located are the same
To merge the elements of two sets a and B, first judge whether the two elements belong to one set (call the issameset method),
a. If b does not belong to the same set, merge and change the pointer pointed up by b to a; Find the top of a collection (representing an element) and mount it on the top of another element
The set structure is represented by a graph pointing up

(2) Illustration

2. The board of merging query

//Parallel search set structure, and method
#include <iostream>
#include <cstring>


using namespace std;

const int maxn = 100;

int par[100]; //When father par[x]=x, X is the root of the tree
int rank[100]; //Tree height

//Initialize n elements
void init(int n)
{
    for(int i=0;i<n;i++)
    {
        par[i] = i;
        rank[i] = 0;
    }
}

//Root of query tree
int find(int x)
{
    if(par[x]==x){
        return x;
    }else {
        return par[x] = find(par[x]);  //In this way, the path can be compressed
    }
}

//Merge the sets to which x and y belong
void unite(int x, int y)
{
    //Find the root element of the two elements
    x = find(x);
    y = find(y);
    if(x==y) return;  //On the same root, belong to the same set, and return directly

    if(rank[x] < rank[y])  //Determine which element is higher in the tree
    {
        par[x] = y;  //The root of x becomes y
    }
    else
    {
        par[y] = x;  //The root of y becomes x
        if(rank[x]==rank[y]) rank[x]++;   //Two trees originally have the same height. If you mount one tree to another, the height needs to be increased by 1 
    }

}

//Judge whether elements a and B belong to the same set
bool same(int x, int y)
{
    return find(x) == find(y);
}

2, Application of parallel search set

(1) P1536 village to village solution

Title Link

1. Algorithm examination of the topic

Joint search set

2. Programming idea

• Two arrays par: used to save the root node of the tree where each village is located; H: H[i] represents the height of the tree with I as the root node. It is used in merging to merge the numbers with small height onto the trees with large height.
• Each village is regarded as a node of a tree. During initialization, each village is an independent tree, and their root node is themselves;
• According to the given road relationship, connect the villages. How to explain the connection between the two villages? Let their root nodes become the same, which can be implemented with the union function.

For example, the root node of the tree where each village is located is saved in the array par. At the beginning, for the village numbered 1, par[1]=1, and for the village numbered 2, par[2]=2 Assuming that there is a road between village 1 and village 2 in the road given in the title, mount the tree where village 2 is located on tree 1, and make the root node of village 2 become 1, that is, par[2]=1 after merging. At this time, the root nodes of village 1 and village 2 are both 1, so they are the same.

• Finally, it is necessary to count which villages are not connected. Under what circumstances are all villages connected? That is, the root nodes of all villages are the same. Set a statistical variable ret to record how many roads need to be built, traverse each village and check whether its root node is the same as that of other villages (Note: assuming that the relationship between village 1 and village 2 has been determined when viewing village 1, it is unnecessary to manage the relationship between village 1 and village 2 when viewing village 2 and other villages). If it is different, ret+1 and connect the two villages with the unite function. The final ret statistical value is the number of roads to be built.

3. Code

#include <iostream>
#include <cstring>
//https://www.luogu.com.cn/problem/P1536
using namespace std;

const int maxn=10005;
int n, m;  //Number of towns n and roads m
int par[maxn]; //Used to save the root node of the tree where each town is located
int H[maxn]; //Used to save the height of the tree

void init(int n) //initialization
{
    for(int i=1;i<=n;i++)
    {
        par[i] = i;
        H[i] = 1;
    }
}
/*
a If you can reach b,c, then the root nodes of a, B and C are the same
*/
int find(int a) //Find root node
{
    if(par[a] == a)
        return a;
    else
        return par[a] = find(par[a]);
}

void unite(int a,int b) //Merge the sets of a and b   
{
    a = find(a);
    b = find(b);

    if(a==b)
        return;

    if(H[a]>=H[b])
    {
        par[b] = a;
        if(H[a]==H[b]) H[a]++;
    }
    else
        par[a] = b;

}

bool isReach(int a, int b) //Judge whether the villages and towns a and b can be reached
{
    return find(a) == find(b);
}

void solve()
{
    //Relationship between receiving roads
    int a, b;
    //Enter the data connected to the road
    for(int i=0;i<m;i++)
    {
        cin >> a >> b;
        unite(a,b);   //Merge a and b
    }
    //How many more roads do you need to connect
    //Traverse every village and town
    int ret=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=i+1;i<=n;i++)
        {
            if(!isReach(i,j))  //If the two villages and towns are not connected, a road is needed
            {
                ret++;
                unite(i,j);
            }

        }
    }

    cout << ret << endl;

}
int main()
{
    while(true)
    {
        cin >> n;
        if(n==0)
            break;
        cin >> m;
        memset(par,0,sizeof(par));
        memset(H, 0, sizeof(par));
        init(n);  //initialization
        //Enter two numbers
        solve();
    }
    return 0;
}

(2) P1551 relatives

Title Link

1. Code

#include <iostream>
#include <cstring>
using namespace std;

const int maxn = 5005;
int par[maxn]; //Root node par[i]=2. The root node of the ith element is 2
int treeHigh[maxn]; //Represents the height of the tree treeHigh[i] represents the height of the tree with I as the root node

//Initialize n elements
void init(int n)
{
    for(int i=1;i<=n;i++)
    {
        par[i] = i;
        treeHigh[i] = 1;
    }
}
//Query tree root
int find(int x)
{
    if(par[x]==x)
        return x;
    else
    {
        par[x] = find(par[x]);
        return par[x];
    }
}

//merge
void unite(int x, int y)
{
    //First find the root node of the x,y element
    x = find(x);
    y = find(y);
    if(x == y) return;
    if(treeHigh[x] >= treeHigh[y])
    {
        par[y] = x;  //Merge to change the root of y into the root of x
        if(treeHigh[x] == treeHigh[y]) treeHigh[x]++;
    }
    else
    {
        par[x] = y; //The root node of x becomes y
    }
}
bool isSameSet(int x, int y)
{
    return find(x) == find(y);
}
int main()
{
    int n, m, p;
    int a, b;
    cin >> n >> m >> p;
    init(n);  //Initialize these n people
    //Enter m relationships
    for (int i = 0; i < m; i++)
    {
        cin >> a >> b;
        //Merge a and B
        unite(a, b);  //Relative merger
    }
    
    for(int j=0;j<p;j++)
    {
        cin >> a >> b;
        if(isSameSet(a,b))
            cout << "Yes" << endl;
        else
            cout << "No" << endl;
    }

    return 0;
}