preface
This competition is a data analysis novice learner development competition organized by Tianchi data platform. The content of the competition is used car price prediction. The data is provided by Tianchi platform. When I first saw this topic, my first reaction was to use the linear regression method. Of course, this is the simplest, and the possible results are not particularly good. Therefore, we use lgb here, Let's have a look
Tip: the following is the main content of this article. The following cases can be used for reference
1, Game question understanding
1.1 overview of competition questions
The competition requires the contestants to establish a model and the transaction price of second-hand cars according to the given data set.
The task of the competition is to predict the transaction price of second-hand cars. The data set can be seen and downloaded after registration. The data comes from the second-hand car transaction record of A trading platform. The total amount of data is more than 40w, including 31 columns of variable information, of which 15 are anonymous variables. In order to ensure the fairness of the competition, 150000 will be selected as the training set, 50000 as the test set A and 50000 as the test set B. at the same time, the information such as name, model, brand and regionCode will be desensitized.
1.2 prediction indicators
The evaluation standard of this competition is MAE(Mean Absolute Error):
M
A
E
=
∑
i
=
1
n
∣
y
i
−
y
^
i
∣
n
MAE=\frac{\sum_{i=1}^{n}\left|y_{i}-\hat{y}_{i}\right|}{n}
MAE=n Σ i=1n ∣ yi − y ^ i ∣ where
y
i
y_{i}
yi represents the third party
i
i
The true value of i samples, where
y
^
i
\hat{y}_{i}
y ^ i stands for the second
i
i
Predicted value of i samples.
Description of evaluation indicators of general problems:
What are the evaluation indicators:
The evaluation index is our numerical quantification of the effect of a model. (it's a bit similar to scoring a commodity evaluation, which is a score between the model effect and the ideal effect)
Generally speaking, the evaluation indicators of classification and regression problems have the following forms:
Common evaluation indicators of classification algorithm are as follows:
- For class II classifiers / classification algorithms, the main evaluation indicators are accuracy,
[Precision, Recall, F-score, Pr curve], ROC-AUC curve. - For multi class classifiers / classification algorithms, the main evaluation indicators are accuracy, [macro average and micro average, F-score].
Common evaluation indicators for regression prediction are as follows:
- Mean Absolute Error (MAE), mean square error (MSE), Mean Absolute Percentage Error (MAPE), root mean square error (root mean square error), R2 (R-Square)
Mean Absolute Error (MAE): Mean Absolute Error, which can better reflect the actual situation of the error between the predicted value and the real value. Its calculation formula is as follows: M A E = 1 N ∑ i = 1 N ∣ y i − y ^ i ∣ MAE=\frac{1}{N} \sum_{i=1}^{N}\left|y_{i}-\hat{y}_{i}\right| MAE=N1i=1∑N∣yi−y^i∣
Mean square error (MSE), mean square error, its calculation formula is: M S E = 1 N ∑ i = 1 N ( y i − y ^ i ) 2 MSE=\frac{1}{N} \sum_{i=1}^{N}\left(y_{i}-\hat{y}_{i}\right)^{2} MSE=N1i=1∑N(yi−y^i)2
The formula of R2(R-Square) is: sum of squares of residuals: S S r e s = ∑ ( y i − y ^ i ) 2 SS_{res}=\sum\left(y_{i}-\hat{y}{i}\right)^{2} SSres = ∑ (yi − y ^ i)2 total average: S S t o t = ∑ ( y i − y ‾ i ) 2 SS{tot}=\sum\left(y_{i}-\overline{y}_{i}\right)^{2} SStot=∑(yi−yi)2
among y ‾ \overline{y} y represents y y The average value of y R 2 R^2 R2 expression is: R 2 = 1 − S S r e s S S t o t = 1 − ∑ ( y i − y ^ i ) 2 ∑ ( y i − y ‾ ) 2 R^{2}=1-\frac{SS_{res}}{SS_{tot}}=1-\frac{\sum\left(y_{i}-\hat{y}{i}\right)^{2}}{\sum\left(y{i}-\overline{y}\right)^{2}} R2=1−SStotSSres=1−∑(yi−y)2∑(yi−y^i)2 R 2 R^2 R2 is used to measure the proportion of the variation of dependent variables that can be explained by independent variables. The value range is 0 ~ 1, R 2 R^2 The closer R2 is to 1, the greater the proportion of the sum of squares in the total sum of squares, the closer the regression line is to each observation point, the more the change of y value is explained by the change of x, and the better the fitting degree of regression is. therefore R 2 R^2 R2 is also known as the statistic of Goodness of Fit.
y i y_{i} yi represents the true value, y ^ i \hat{y}{i} y ^ i represents the predicted value, y ‾ i \overline{y}{i} y i represents the sample mean value. The higher the score, the better the fitting effect.
2, baseline
1. Import and storage
import numpy as np
import pandas as pd
import warnings
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.special import jn
from IPython.display import display, clear_output
import time
warnings.filterwarnings('ignore')
%matplotlib inline
## Model predicted
from sklearn import linear_model
from sklearn import preprocessing
from sklearn.svm import SVR
from sklearn.ensemble import RandomForestRegressor,GradientBoostingRegressor
## Data dimensionality reduction processing
from sklearn.decomposition import PCA,FastICA,FactorAnalysis,SparsePCA
import lightgbm as lgb
import xgboost as xgb
## Parameter search and evaluation
from sklearn.model_selection import GridSearchCV,cross_val_score,StratifiedKFold,train_test_split
from sklearn.metrics import mean_squared_error, mean_absolute_error
2. Read in data
The code is as follows (example):
## Read data through pandas (pandas is a very friendly data reading function library)
Train_data = pd.read_csv('C:\\Users\\TINKPAD\\Desktop\\python_work\\kaggle\Used car transaction price forecast\\used_car_train_20200313.csv', sep=' ')
TestA_data = pd.read_csv('C:\\Users\\TINKPAD\\Desktop\\python_work\\kaggle\Used car transaction price forecast\\used_car_testB_20200421.csv', sep=' ')
## Size information of output data
print('Train data shape:',Train_data.shape)
print('TestA data shape:',TestA_data.shape)
Train data shape: (150000, 31) TestA data shape: (50000, 30)
## Pass head() briefly browses the form of the read data Train_data.head()
SaleID name regDate model ... v_11 v_12 v_13 v_14 0 0 736 20040402 30.0 ... 2.804097 -2.420821 0.795292 0.914762 1 1 2262 20030301 40.0 ... 2.096338 -1.030483 -1.722674 0.245522 2 2 14874 20040403 115.0 ... 1.803559 1.565330 -0.832687 -0.229963 3 3 71865 19960908 109.0 ... 1.285940 -0.501868 -2.438353 -0.478699 4 4 111080 20120103 110.0 ... 0.910783 0.931110 2.834518 1.923482 [5 rows x 31 columns]
## Pass info() briefly shows the corresponding data column names and the missing information of NAN Train_data.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 150000 entries, 0 to 149999 Data columns (total 31 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 SaleID 150000 non-null int64 1 name 150000 non-null int64 2 regDate 150000 non-null int64 3 model 149999 non-null float64 4 brand 150000 non-null int64 5 bodyType 145494 non-null float64 6 fuelType 141320 non-null float64 7 gearbox 144019 non-null float64 8 power 150000 non-null int64 9 kilometer 150000 non-null float64 10 notRepairedDamage 150000 non-null object 11 regionCode 150000 non-null int64 12 seller 150000 non-null int64 13 offerType 150000 non-null int64 14 creatDate 150000 non-null int64 15 price 150000 non-null int64 16 v_0 150000 non-null float64 17 v_1 150000 non-null float64 18 v_2 150000 non-null float64 19 v_3 150000 non-null float64 20 v_4 150000 non-null float64 21 v_5 150000 non-null float64 22 v_6 150000 non-null float64 23 v_7 150000 non-null float64 24 v_8 150000 non-null float64 25 v_9 150000 non-null float64 26 v_10 150000 non-null float64 27 v_11 150000 non-null float64 28 v_12 150000 non-null float64 29 v_13 150000 non-null float64 30 v_14 150000 non-null float64 dtypes: float64(20), int64(10), object(1) memory usage: 35.5+ MB
## Pass columns view column names Train_data.columns
Index(['SaleID', 'name', 'regDate', 'model', 'brand', 'bodyType', 'fuelType',
'gearbox', 'power', 'kilometer', 'notRepairedDamage', 'regionCode',
'seller', 'offerType', 'creatDate', 'price', 'v_0', 'v_1', 'v_2', 'v_3',
'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12',
'v_13', 'v_14'],
dtype='object')
## Pass describe() can view some statistical information of the numerical characteristic column Train_data.describe()
3. Feature and label construction
numerical_cols = Train_data.select_dtypes(exclude = 'object').columns print(numerical_cols)
Index(['SaleID', 'name', 'regDate', 'model', 'brand', 'bodyType', 'fuelType',
'gearbox', 'power', 'kilometer', 'regionCode', 'seller', 'offerType',
'creatDate', 'price', 'v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6',
'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13', 'v_14'],
dtype='object')
categorical_cols = Train_data.select_dtypes(include = 'object').columns print(categorical_cols)
Index(['notRepairedDamage'], dtype='object')
##2) Build training and test samples
## Select feature column
feature_cols = [col for col in numerical_cols if col not in ['SaleID','name','regDate','creatDate','price','model','brand','regionCode','seller']]
feature_cols = [col for col in feature_cols if 'Type' not in col]
## Training sample column, training sample column and feature column
X_data = Train_data[feature_cols]
Y_data = Train_data['price']
X_test = TestA_data[feature_cols]
print('X train shape:',X_data.shape)
print('X test shape:',X_test.shape)
X train shape: (150000, 18) X test shape: (50000, 18)
## A statistical function is defined to facilitate subsequent information statistics
def Sta_inf(data):
print('_min',np.min(data))
print('_max:',np.max(data))
print('_mean',np.mean(data))
print('_ptp',np.ptp(data))
print('_std',np.std(data))
print('_var',np.var(data))
##3) Basic distribution information of statistical labels
print('Sta of label:')
Sta_inf(Y_data)
Sta of label: _min 11 _max: 99999 _mean 5923.327333333334 _ptp 99988 _std 7501.973469876438 _var 56279605.94272992
## Draw the statistical chart of labels and view the distribution of labels plt.hist(Y_data) plt.show() plt.close()
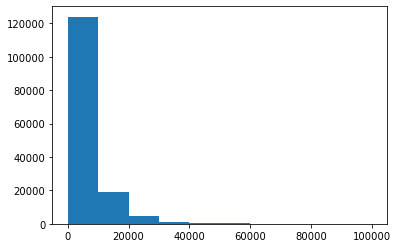
##4) The default value is filled with - 1 X_data = X_data.fillna(-1) X_test = X_test.fillna(-1)
4. Model training and prediction
##1) Use xgb for 50% cross validation to check the parameter effect of the model
## xgb-Model
xgr = xgb.XGBRegressor(n_estimators=120, learning_rate=0.1, gamma=0, subsample=0.8,\
colsample_bytree=0.9, max_depth=7) #,objective ='reg:squarederror'
scores_train = []
scores = []
## 5-fold cross validation method
sk=StratifiedKFold(n_splits=5,shuffle=True,random_state=0)
for train_ind,val_ind in sk.split(X_data,Y_data):
train_x=X_data.iloc[train_ind].values
train_y=Y_data.iloc[train_ind]
val_x=X_data.iloc[val_ind].values
val_y=Y_data.iloc[val_ind]
xgr.fit(train_x,train_y)
pred_train_xgb=xgr.predict(train_x)
pred_xgb=xgr.predict(val_x)
score_train = mean_absolute_error(train_y,pred_train_xgb)
scores_train.append(score_train)
score = mean_absolute_error(val_y,pred_xgb)
scores.append(score)
print('Train mae:',np.mean(score_train))
print('Val mae',np.mean(scores))
Train mae: 622.836567743063 Val mae 714.0856746034109
##2) Define xgb and lgb model functions
def build_model_xgb(x_train,y_train):
model = xgb.XGBRegressor(n_estimators=150, learning_rate=0.1, gamma=0, subsample=0.8,\
colsample_bytree=0.9, max_depth=7) #, objective ='reg:squarederror'
model.fit(x_train, y_train)
return model
def build_model_lgb(x_train,y_train):
estimator = lgb.LGBMRegressor(num_leaves=127,n_estimators = 150)
param_grid = {
'learning_rate': [0.01, 0.05, 0.1, 0.2],
}
gbm = GridSearchCV(estimator, param_grid)
gbm.fit(x_train, y_train)
return gbm
##3) The segmentation data set (Train,Val) is used for model training, evaluation and prediction
## Split data with val
x_train,x_val,y_train,y_val = train_test_split(X_data,Y_data,test_size=0.3)
print('Train lgb...')
model_lgb = build_model_lgb(x_train,y_train)
val_lgb = model_lgb.predict(x_val)
MAE_lgb = mean_absolute_error(y_val,val_lgb)
print('MAE of val with lgb:',MAE_lgb)
Train lgb... MAE of val with lgb: 691.2926210859479
print('Predict lgb...')
model_lgb_pre = build_model_lgb(X_data,Y_data)
subA_lgb = model_lgb_pre.predict(X_test)
print('Sta of Predict lgb:')
Sta_inf(subA_lgb)
Predict lgb... Sta of Predict lgb: _min -589.8793550785414 _max: 90760.26063584947 _mean 5906.935218383807 _ptp 91350.13999092802 _std 7344.644970956768 _var 53943809.749400534
print('Train xgb...')
model_xgb = build_model_xgb(x_train,y_train)
val_xgb = model_xgb.predict(x_val)
MAE_xgb = mean_absolute_error(y_val,val_xgb)
print('MAE of val with xgb:',MAE_xgb)
Train xgb... MAE of val with xgb: 715.2890582658079
Predict xgb... Sta of Predict xgb: _min -318.20892 _max: 90140.625 _mean 5910.7607 _ptp 90458.836 _std 7345.965 _var 53963196.0
##4) The results of the two models are weighted and fused
## Here we adopt a simple weighted fusion method
val_Weighted = (1-MAE_lgb/(MAE_xgb+MAE_lgb))*val_lgb+(1-MAE_xgb/(MAE_xgb+MAE_lgb))*val_xgb
val_Weighted[val_Weighted<0]=10 # Since we found that the predicted minimum value has a negative number, but in the real case, if the price is negative, it does not exist, so we made the corresponding post correction
print('MAE of val with Weighted ensemble:',mean_absolute_error(y_val,val_Weighted))
sub_Weighted = (1-MAE_lgb/(MAE_xgb+MAE_lgb))*subA_lgb+(1-MAE_xgb/(MAE_xgb+MAE_lgb))*subA_xgb
MAE of val with Weighted ensemble: 689.3545169592032
## View statistics of predicted values plt.hist(Y_data) plt.show() plt.close()
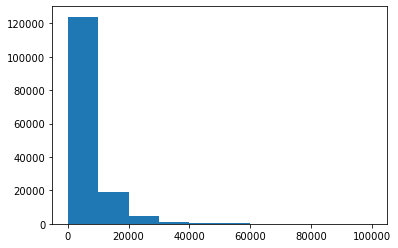
##5) Output results
sub = pd.DataFrame()
sub['SaleID'] = TestA_data.SaleID
sub['price'] = sub_Weighted
sub.to_csv('./sub_Weighted.csv',index=False)
sub.head()
SaleID price 0 200000 1177.369198 1 200001 1806.742061 2 200002 8560.577630 3 200003 1346.459235 4 200004 2074.334952
Final score:
summary
From this baseline, we can see that the prediction results are obtained by using the weighted fusion of the two models, and the final score is higher, which also shows that the above code has a lot of room for progress