Basic introduction
- Huffman coding, also known as optimal coding, is a coding method and also belongs to a program algorithm.
- Huffman coding is one of the classical applications of Huffman tree in telecommunications.
- Huffman coding is widely used in data file compression, and its compression rate is usually between 20% ~ 90%.
- Huffman coding is a kind of variable word length coding. It is a kind of time code. It is a coding method proposed by Huffman in 1952, which is called the best coding.
Principle analysis
- Fixed length coding
- String: i like java, 11 characters in total
- Corresponding ascii code values: 105, 32108105107101, 32106, 97118, 97
- Corresponding binary: 01101001 00100000 0110100 0110100 01101001 01100100000 01101010 0110001 011011010001 011011011011011011011011011011011011011
- 88bit is required for binary transmission
- Variable length coding
- String: i like java, 11 characters in total
- "": 2, a: 2, i: 2, e: 1, k: 1, l: 1, j: 1, v: 1 (the number of times corresponding to each character)
- : 0, a: 1, i: 10, e: 11, k: 110, l: 111, j: 1110, v: 1111
- The bit stream transmitted is: 100111101110111111 (24bit)
- However, there will be objections to this coding, such as whether the first two bits of 10 are 1, 0 or 10, which is related to the coding method. Some codes are prefixes of other codes, so they are not uniquely decodeable
- Huffman coding - best coding (only decodeable, even if code)
- String: i like java, 11 characters in total
- "": 2, a: 2, i: 2, e: 1, k: 1, l: 1, j: 1, v: 1 (the number of times corresponding to each character)
- Take the number of occurrences as the weight, construct a Huffman number, and then encode it.
Steps:
Each character is regarded as a node (a tree), and the number of occurrences is used as the weight to sort from small to large
Take out the smallest two nodes and add their weights to form a new root node.
Sort the weights of the above new nodes again
Repeat the above steps until all the data is processed and there is only one tree left.
As shown in the figure below:
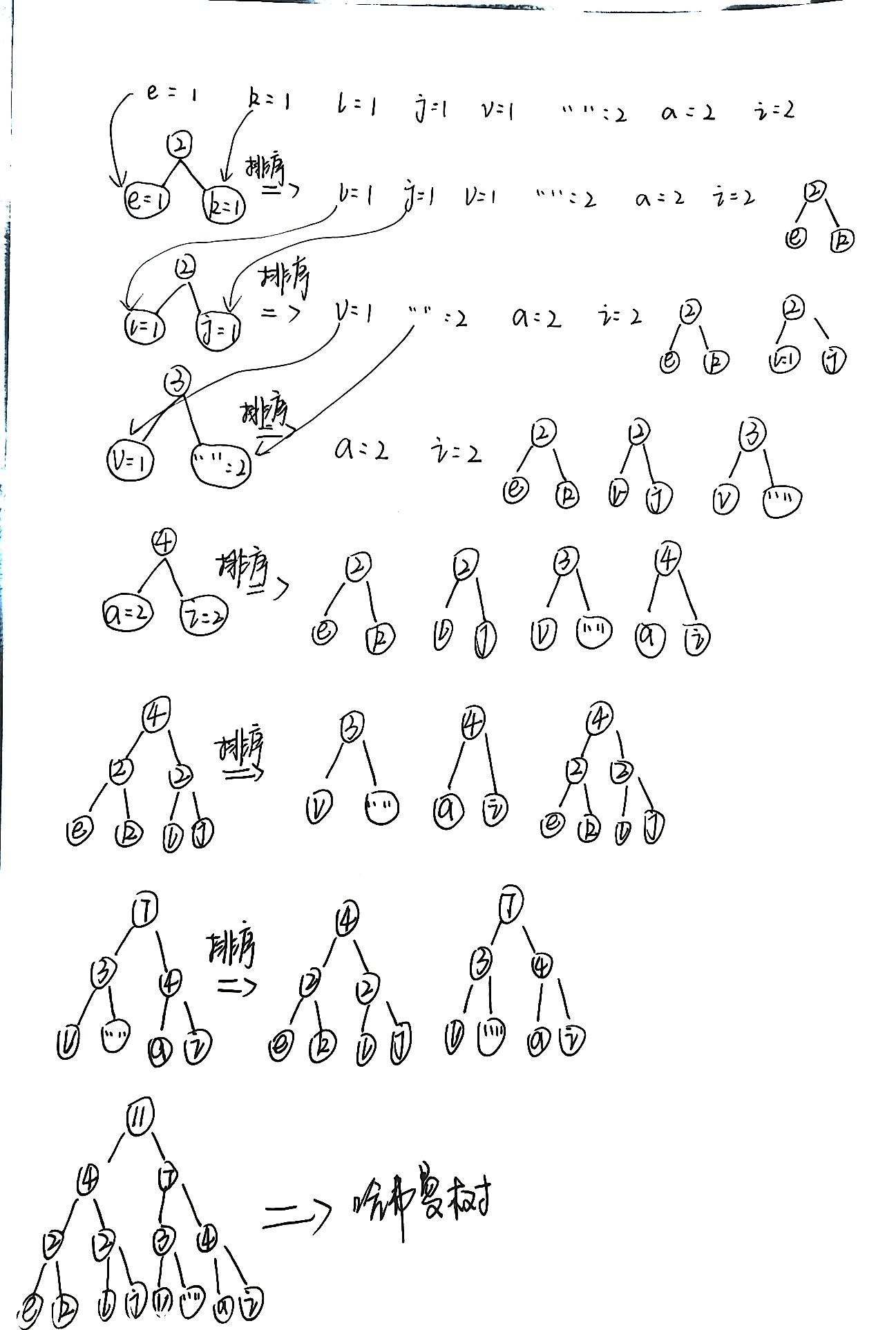
According to the Huffman tree, each character is encoded. The path to the left is 0 and the path to the right is 1. The encoding is as follows:
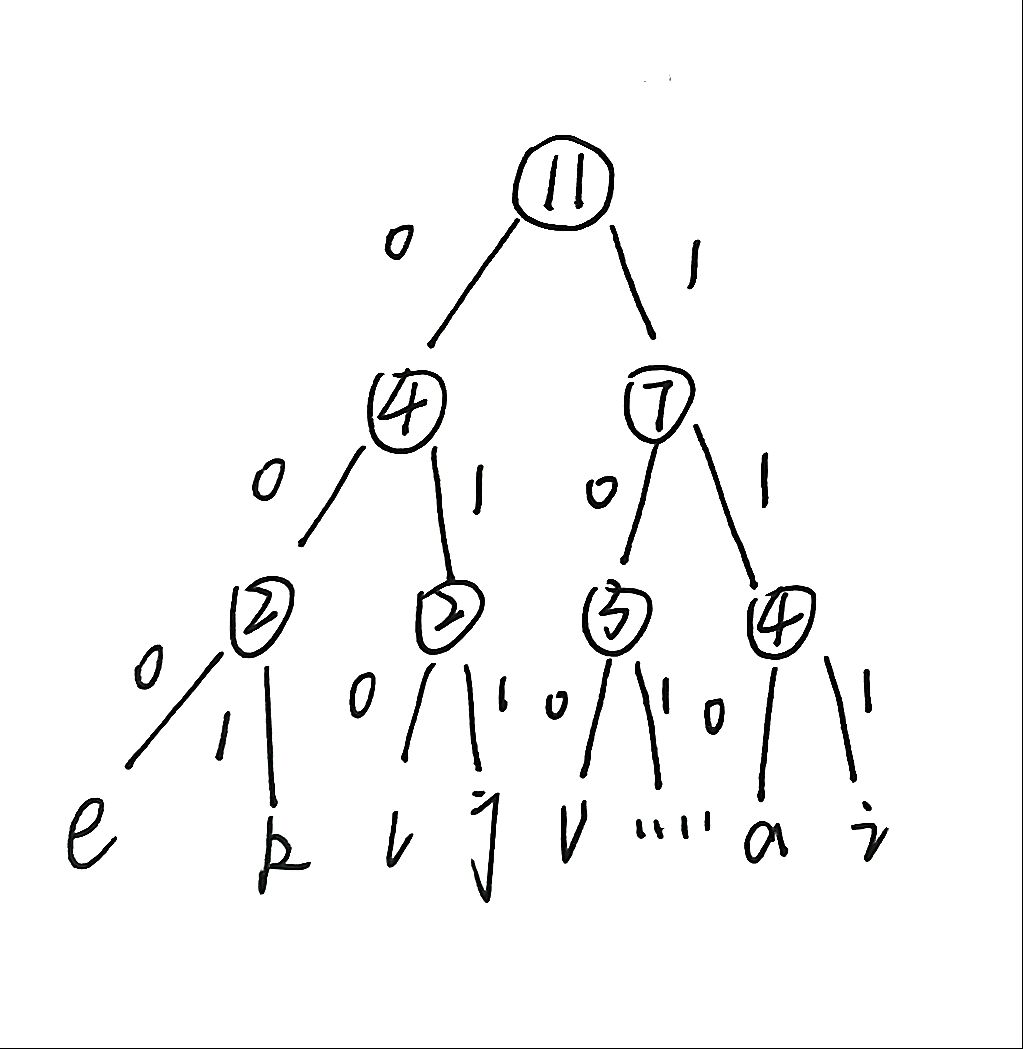
You can get the codes of each:
e: 000, k: 001 ,l: 010,j : 011, v: 100, " " : 101,a:110,i:111
According to the above coding, we can get its binary string
i like java
111101010111001000101011110100110 (33bit)
Any codeword is not other prefix, but also real-time code
Note: because the occurrence times of each character are not different, they are all three digits. If the occurrence times of characters are very different, it will be obvious that the character with more occurrence times has a shorter code
matters needing attention:
According to the different positions of nodes with the same weight, the corresponding Huffman code is not exactly the same, but the length of the final Huffman code is the same.
In the above, I always put the synthesized new binary tree behind the same weight. If it is placed in front, it will generate a different binary tree.
Let's take a look at the specific code implementation:
First, we create a Node:
It should be noted that the Node node implements Comparable because we need to sort the nodes
package Huffmanzip;
/**
* Build a Node and save the corresponding value, that is, the code value
* @ClassName: Node
* @Author
* @Date 2022/1/24
*/
public class Node implements Comparable<Node> {
//The corresponding data field stores characters
private Byte data ;
//The weight is the number of occurrences
private int weight ;
//Left and right child nodes
private Node left;
private Node right;
//Construction method
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
public Byte getData() {
return data;
}
public void setData(Byte data) {
this.data = data;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
@Override
public String toString() {
return "Node{" +
"data=" + data +
", weight=" + weight +
'}';
}
@Override
public int compareTo(Node o) {
return this.weight - o.weight;
}
//Preorder traversal
public void preOrder(Node node){
if (node!=null){
System.out.println(node);
preOrder(node.left);
preOrder(node.right);
}
}
}
Then we write a method: convert all the incoming characters into nodes, use map to count the number of occurrences of the same node, and then store the node value and weight in the list set for our comparison
package Huffmanzip;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
/**
* Used to get the linked list corresponding to byte []
* @ClassName: GetList
* @Author
* @Date 2022/1/24
*/
public class GetList {
/**
* Build a linked list based on the incoming bytes
* @param bytes Bytes split from strings
* @return The final linked list
*/
public static List<Node> getList(byte[] bytes){
List<Node> list = new ArrayList<>();
//Define a Map to count the number
Map<Byte,Integer> map = new HashMap<>();
//Ergodic statistics
for (byte b : bytes){
if (map.containsKey(b)){
map.put(b,map.get(b)+1);
}else {
map.put(b,1);
}
}
//Traverse the map to get its corresponding key value pair
for (Map.Entry<Byte,Integer> entry : map.entrySet()){
list.add(new Node(entry.getKey(), entry.getValue()));
}
return list;
}
}
We have got all the nodes above, which are saved in a list set. Next, we need to change the nodes into a Huffman tree
We write a method: according to the linked list passed in, it is transformed into a Huffman tree and returned to the root node
package Huffmanzip;
import java.util.Collections;
import java.util.List;
/**
* Create a Huffman tree according to the linked list passed in
* @ClassName: CreateHuffmanTree
* @Author
* @Date 2022/1/24
*/
public class CreateHuffmanTree {
public static Node creat(List<Node> nodes){
while (nodes.size()>1){
//Sort first
Collections.sort(nodes);
//Get the minimum two nodes
Node left = nodes.get(0);
Node right = nodes.get(1);
//Generate a new node
Node parent = new Node(null,left.getWeight()+right.getWeight());
parent.setLeft(left);
parent.setRight(right);
//Remove old nodes and add new nodes
nodes.remove(left);
nodes.remove(right);
nodes.add(parent);
}
return nodes.get(0);
}
//Preorder traversal method
public static void preOrder(Node node){
node.preOrder(node);
}
}
We have generated the Huffman tree above, and then we write a method: according to the Huffman tree, return the corresponding byte and the corresponding code
//Coding method
package Huffmanzip;
import java.util.HashMap;
import java.util.Map;
/**
* @ClassName: HuffmanCoding
* @Author
* @Date 2022/1/24
*/
public class HuffmanCoding {
/**
*
* @param node Root node
* @param code Is the code 0 or 1
* @param str Code splicing
* @param ans Correspondence between returned bytes and codes
*/
static Map<Byte,String> ans = new HashMap<>();
public static Map<Byte,String> getHuffmanCoding(Node node,String code,StringBuilder str){
StringBuilder sb = new StringBuilder(str);
sb.append(code);
if (node!=null){
if (node.getData()==null){//Description is not a leaf node
//towards the left
getHuffmanCoding(node.getLeft(),"0",sb);
getHuffmanCoding(node.getRight(),"1",sb);
}else {
ans.put(node.getData(),sb.toString());
}
}
return ans;
}
}
The last step is to return the encoded byte array according to the original string and the encoding comparison table
package Huffmanzip;
import java.util.Map;
/**
* @ClassName: ByteToHuffmanCode
* @Author
* @Date 2022/1/24
*/
public class ByteToHuffmanCode {
/**
* Convert the byte array of the string corresponding to the original data into the encoded byte array
* @param bytes Byte array corresponding to original data
* @param codes Coding table
* @return Encoded byte array
*/
public static byte[] byteToHuffmanCode(byte[] bytes, Map<Byte,String> codes){
//Used to splice codes
StringBuilder sb = new StringBuilder();
//Splice and get the corresponding code according to the bytes
for (byte b : bytes){
sb.append(codes.get(b));
}
//Process after splicing
//Length of new array
int length = (sb.length() + 7) / 8 ;
//New array
byte[] ans = new byte[length];
int index = 0;
for (int i = 0; i < sb.length();i+=8){
String string;
if (i+8>sb.length()){
string = sb.substring(i);
}else {
string = sb.substring(i,i+8);
}
ans[index++] = (byte) Integer.parseInt(string,2);
}
return ans;
}
}
In this way, we get the encoded byte array.
Finally, we encapsulate all the above methods in one class. We only need to pass in the string to get the corresponding compressed byte array.
package Huffmanzip;
import java.nio.charset.StandardCharsets;
import java.util.List;
import java.util.Map;
/**
* Convert element data to compressed bytes
* @ClassName: HuffmanCodingCompress
* @Author
* @Date 2022/1/24
*/
public class HuffmanCodingCompress {
public static byte[] compress(String str){
byte[] bytes = str.getBytes(StandardCharsets.UTF_8);
//Got the list
List<Node> list = GetList.getList(bytes);
//Build huffmanTree to get the root node of the tree
Node root = CreateHuffmanTree.creat(list);
//Encode and save the encoded value in the map
Map<Byte, String> huffmanCoding = HuffmanCoding.getHuffmanCoding(root, "", new StringBuilder());
// for (Map.Entry<Byte,String> entry : huffmanCoding.entrySet()){
// System.out.println(entry.getKey()+": "+entry.getValue());
// }
return ByteToHuffmanCode.byteToHuffmanCode(bytes, huffmanCoding);
}
}
Test code:
public class Test {
public static void main(String[] args) {
String str = "i like java";
byte[] bytes = HuffmanCodingCompress.compress(str);
for (byte b : bytes) {
System.out.print( b + " ");
}
}
}
result: