Title: if there is a function rand(0,7) - take a natural number randomly from 0 to 7, ask how to use this function to construct rand(0,10) - take a natural number randomly from 0 to 10.

PS: this topic is implemented on the premise that rand(10) has no ready-made function. It must be constructed through rand(7)

(Note: pay attention to the distribution of the function, or use Monte Carlo method)

Wrong idea:

Let A be rand(0,7) and B be rand(0,7). These two numbers are randomly obtained from 0 to 7, and then the obtained results are added. If the result is greater than 10, it will be executed again, otherwise the added result will be returned. The python implementation code is as follows:

import random
def rand_10():
    C = 11
    while C>10:
        A = random.randint(0,7)    
        B = random.randint(0,7)
        C = A+B
    return C

python executes 0 times and obtains the following results:

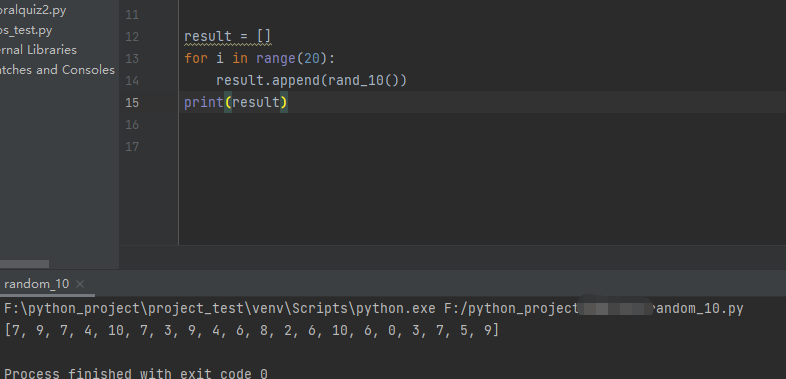
The result of this problem-solving idea is a natural number between 0 and 10, but the result is wrong. First look at the correct problem-solving idea, and then explain why the value is wrong.

Correct thinking:

Let a be rand(0,7) and B be rand(0,7), both of which are random numbers from 0 to 7. A is the high-order (ten bits) and B is the low-order (one bit). Calculate the value of A*8+B to get an integer within 63, and the obtained data is still evenly distributed. Then we modulus the result to 11 to get a natural number within 0 to 10, but modulus 11 to 63 results to 8, then 0 to 8 will result more than 9 and 10. Therefore, we only take the number from 0 to 54 to modulus 11, and the code is as follows:

def rand_10_2():
    rand_all = 55
    while rand_all >= 55:    #The maximum value of A*8+B is 63, and module 11 gets 8,0 ~ 8 more than 9,10. Therefore, when it is calculated to 54, each number appears 5 times on average
        A = random.randint(0,7)   #Octal high bit
        B = random.randint(0, 7)  #Octal low
        rand_all = A*8+B
        C = rand_all%11    #Natural number from 0 to 10, including 0 and 10
    return C

It is also executed 20 times, and the number obtained is an integer between 0 and 10.

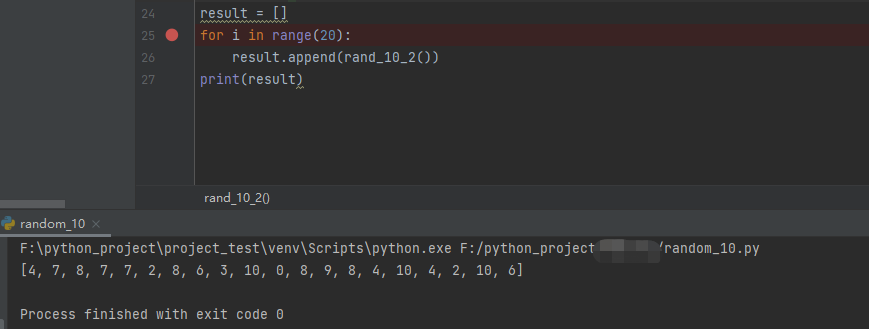
, verification results:

To verify which of the two results is right, first of all, we have to understand that rand function is a function that randomly takes a number from a group of numbers, so it must obey uniform distribution, so as to ensure that the probability of each number is the same. We use Monte Carlo method to verify, that is, simulate 100000 or more times, then count the number of times of each number, and look at the histogram of the statistical results. From the histogram, we can see whether it obeys uniform distribution.

1. Verify that the functions of the system obey the distribution, and the code is as follows:

import random
import numpy as np
import matplotlib.pyplot as plt

y = [0]*8      # Store the number of values obtained by rand function
for i in range(100000):   # Take values from 100000 data for verification
    num_1 = random.randint(0,7)
    for j in range(0,8):
        if j == num_1:
            y[j] +=1

x = np.linspace(0, 7, num=8)
plt.bar(x, y, align='center', alpha=0.7)
plt.xlabel('num for rand')
plt.ylabel('count for rand')
plt.title('rand(7)')
plt.show()             #The results are displayed by histogram

The histogram obtained after operation is as follows:

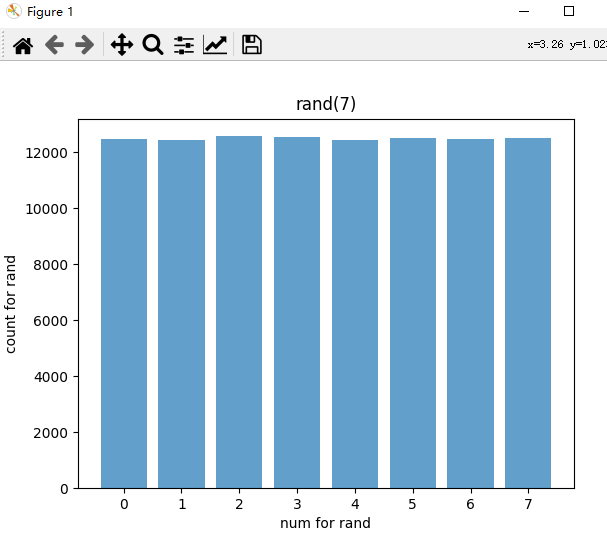
The results of 8 numbers are basically equal, which shows that the functions of python system obey uniform distribution.

2. The method of adding two Rand functions to obtain rand(10) is verified by this method

The code is as follows:

import random
import numpy as np
import matplotlib.pyplot as plt

def rand_10():
    C = 11
    while C>10:
        A = random.randint(0,7)
        B = random.randint(0,7)
        C = A+B
    return C

y = [0]*11      # Store the number of values obtained by rand function
for i in range(150000):   # Take values from 100000 data for verification
    num_1 = rand_10()
    for j in range(0,11):
        if j == num_1:
            y[j] +=1

x = np.linspace(0, 10, num=11)
plt.bar(x, y, align='center', alpha=0.7)
plt.xlabel('num for rand')
plt.ylabel('count for rand')
plt.title('rand(10)_add')
plt.show()             #The results are displayed by histogram

The histogram obtained after operation is as follows: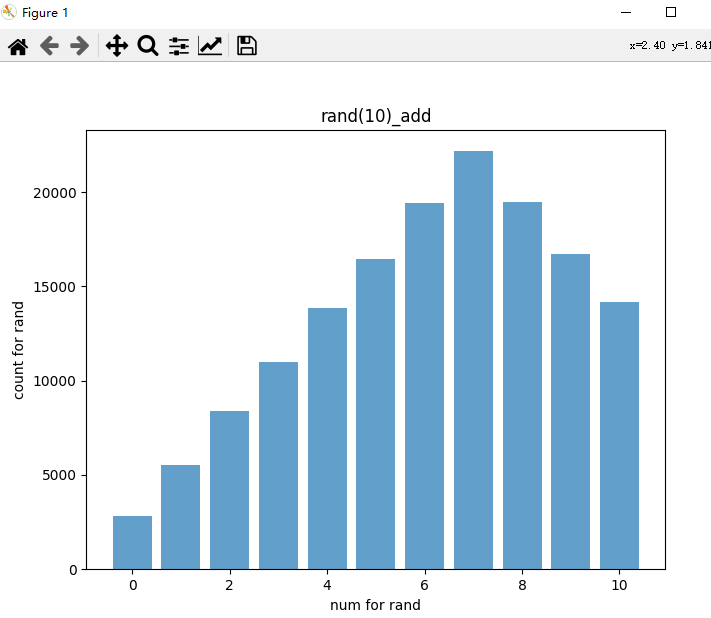

It can be seen from the figure that this distribution is not uniform distribution, but obeys Poisson distribution, i.e. normal distribution. As for why it obeys this distribution, I will explain it later.

3. The results obtained by the method of high * hexadecimal + low are verified

def rand_10_2():
    rand_all = 55
    while rand_all >= 55:    #The maximum value of A*8+B is 63. Module 11 gets 8,0 ~ 8 more than 9,10. Therefore, when it is calculated to 54, each number appears 5 times on average
        A = random.randint(0,7)   #High octal
        B = random.randint(0, 7)  #Octal low
        rand_all = A*8+B
        C = rand_all%11    #Natural number from 0 to 10, including 0 and 10
    return C

y = [0]*11      # Store the number of values obtained by rand function
for i in range(150000):   # Take values from 100000 data for verification
    num_1 = rand_10_2()
    for j in range(0,11):
        if j == num_1:
            y[j] +=1

x = np.linspace(0, 10, num=11)
plt.bar(x, y, align='center', alpha=0.7)
plt.xlabel('num for rand')
plt.ylabel('count for rand')
plt.title('rand(10)_ocx')
plt.show()             #The results are displayed by histogram

The results obtained after operation are as follows:

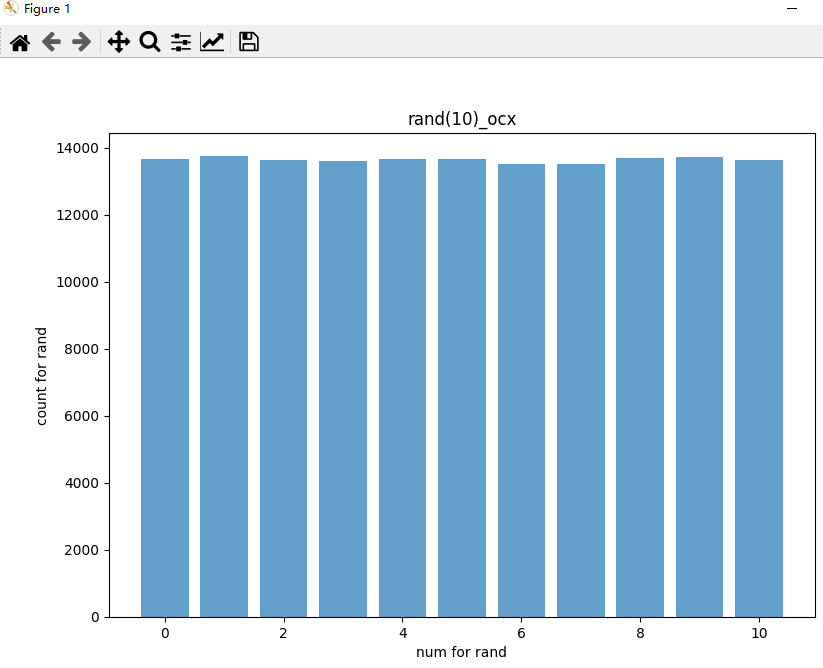
It can be seen from the histogram that the results obey uniform distribution.