In Understanding data structure graph s In learning, we learned the basic concepts of diagrams and learned them by learning. Dijkstra Shortest Path Algorithm And DFS (depth-first traversal) and BFS (breadth-first traversal) You can learn how to find the shortest path in the graph.Why study maps?In scheduling tasks, the concept of graph is used extensively to deal with the dependencies of tasks. Therefore, in order to understand the principle thoroughly, it is necessary to study it roughly.In addition, maps are also used extensively in machine learning, such as knowledge mapping, recommendation systems, and so on.

Next, we manipulate the graph through the jgrapht library.The jgrapht library provides the ability to perform graph operations in java at https://github.com/jgrapht/jgrapht.Here we will learn how to use this library by using some small chestnuts.

Example 1: Basic API

In the graph, there are some basic concepts, such as Vertex, edge, degree, ring, acyclic.If you don't, you can do so in the articles mentioned above.Okay, let's do it.

In the code, the directed graph shown in the following figure is described

 

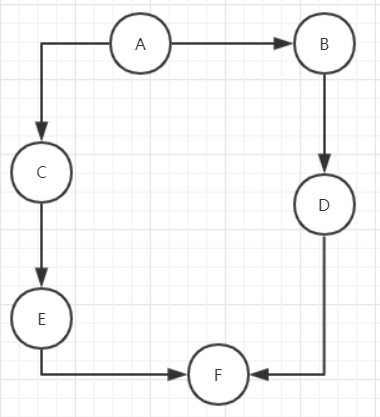
    @Test
    public void testOtherAPI() {
        String a = "A";
        String b = "B";
        String c = "C";
        String d = "D";
        String e = "E";
        String f = "F";

        // Build Diagram
        Graph<String, DefaultEdge> g = new DefaultDirectedGraph<>(DefaultEdge.class);
        // add vertex
        g.addVertex(a);
        g.addVertex(b);
        g.addVertex(c);
        g.addVertex(d);
        g.addVertex(e);
        g.addVertex(f);
        // Add Edge
        g.addEdge(a, b);
        g.addEdge(a, c);
        g.addEdge(b, d);
        g.addEdge(c, e);
        g.addEdge(d, f);
        g.addEdge(e, f);

        // degree
        System.out.println(g.degreeOf(a)); // output: 2
        System.out.println(g.inDegreeOf(a)); // Initiation output: 0
        System.out.println(g.outDegreeOf(a)); // Initiation output: 2

        // Graphs Tool Class
        // List of successor nodes to the current vertex output: [B, C]
        System.out.println(Graphs.successorListOf(g, a));
        // List of successor nodes to the current vertex output: [D, E]
        System.out.println(Graphs.predecessorListOf(g, f));

        // Operation of Ring in Diagram
        CycleDetector<String, DefaultEdge> cycleDetector = new CycleDetector<>(g);
        // Is there a ring output in the probe map: false
        System.out.println(cycleDetector.detectCycles());
        // Find the ring output in the diagram: []
        System.out.println(cycleDetector.findCycles());
    }

Example 2: Directed graph

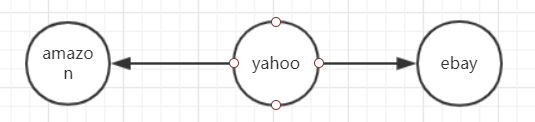
    @Test
    public void testDirectedGraph() {
        // create a graph based on URL objects
        Graph<URL, DefaultEdge> hrefGraph = createHrefGraph();

        // note directed edges are printed as: (<v1>,<v2>)
        // Print all paths, default is that the first edge added is the start vertex
        // The first [] is the number of display vertices; the second [] is the path
        // Print ([http://www.amazon.com, http://www.yahoo.com, http://www.ebay.com], [(http://www.yahoo.com,http://www.amazon.com), (http://www.yahoo.com,http://www.ebay.com)])
        System.out.println(hrefGraph.toString());
    }

    private static Graph<URL, DefaultEdge> createHrefGraph() {
        Graph<URL, DefaultEdge> g = new DefaultDirectedGraph<>(DefaultEdge.class);

        try {
            URL amazon = new URL("http://www.amazon.com");
            URL yahoo = new URL("http://www.yahoo.com");
            URL ebay = new URL("http://www.ebay.com");

            // add the vertices
            // vertex
            g.addVertex(amazon);
            g.addVertex(yahoo);
            g.addVertex(ebay);

            // edge
            // add edges to create linking structure
            g.addEdge(yahoo, amazon);
            g.addEdge(yahoo, ebay);
        } catch (MalformedURLException e) {
            e.printStackTrace();
        }
        return g;
    }

Example 3: The breadth-first and depth-first algorithms traverse directed acyclic graphs

    /**
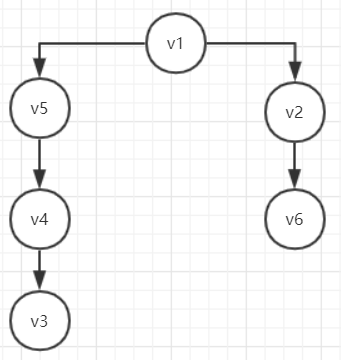
     * Test breadth first traversal
     *
     * ([v1, v2, v3, v4, v5], [(v1,v5), (v5,v3), (v3,v4), (v1,v2), (v4,v2)])
     * []
     * [v2, v3, v4, v5]
     * v1
     * v5
     * v2
     * v3
     * v6
     * v4
     */
    @Test
    public void testBreadthFirstIterator() {
        DirectedAcyclicGraph<String, DefaultEdge> dag = createGraph();
        System.out.println(dag);
        System.out.println(dag.getAncestors("v1"));
        System.out.println(dag.getDescendants("v1"));

        BreadthFirstIterator<String, DefaultEdge> bfi = new BreadthFirstIterator<>(dag, "v1");
        while (bfi.hasNext()) {
            System.out.println(bfi.next());
        }
    }

    /**
     ([v1, v2, v3, v4, v5], [(v1,v5), (v5,v3), (v3,v4), (v1,v2), (v4,v2)])
     []
     [v2, v3, v4, v5]
     v1
     v2
     v6
     v5
     v3
     v4
     * Test Depth First Traversal
     */
    @Test
    public void testDepthFirstIterator() {
        DirectedAcyclicGraph<String, DefaultEdge> dag = createGraph();
        System.out.println(dag);
        System.out.println(dag.getAncestors("v1"));
        System.out.println(dag.getDescendants("v1"));

        DepthFirstIterator<String, DefaultEdge> dfi = new DepthFirstIterator<>(dag, "v1");
        while (dfi.hasNext()) {
            System.out.println(dfi.next());
        }
    }

    /**
     * DAG Directed acyclic graph
     */
    private static DirectedAcyclicGraph<String, DefaultEdge> createGraph() {
        DirectedAcyclicGraph<String, DefaultEdge> g = new DirectedAcyclicGraph<>(DefaultEdge.class);
        String v1 = "v1";
        String v2 = "v2";
        String v3 = "v3";
        String v4 = "v4";
        String v5 = "v5";
        String v6 = "v6";

        // add the vertices
        g.addVertex(v1);
        g.addVertex(v2);
        g.addVertex(v3);
        g.addVertex(v4);
        g.addVertex(v5);
        g.addVertex(v6);

        // If a ring appears, throw the exception IllegalArgumentException
        // add edges to create a circuit
        g.addEdge(v1, v5);
        g.addEdge(v5, v3);
        g.addEdge(v3, v4);
        g.addEdge(v1, v2);
        g.addEdge(v2, v6);

        return g;
    }

Example 4: Dijkstra algorithm for shortest path

    @Test
    public void testShortestPath() {
        Graph<String, DefaultEdge> g2 = new DefaultDirectedGraph<>(DefaultEdge.class);

        String v1 = "v1";
        String v2 = "v2";
        String v3 = "v3";

        // add the vertices
        g2.addVertex(v1);
        g2.addVertex(v2);
        g2.addVertex(v3);


        // v1 -> v2 -> v3
        // add edges to create a circuit
        g2.addEdge(v1, v2);
        g2.addEdge(v2, v3);

        DijkstraShortestPath shortestPath = new DijkstraShortestPath(g2);

        ShortestPathAlgorithm.SingleSourcePaths paths = shortestPath.getPaths(v2);

        System.out.println(paths.toString());

        GraphPath<Integer, DefaultWeightedEdge> shortestPath1 = shortestPath.getPath(v1, v3);
        GraphPath<Integer, DefaultWeightedEdge> shortestPath2 = shortestPath.getPath(v1, v2);
        GraphPath<Integer, DefaultWeightedEdge> shortestPath3 = shortestPath.getPath(v1, v1);
        GraphPath<Integer, DefaultWeightedEdge> shortestPath4 = shortestPath.getPath(v2, v1);
        GraphPath<Integer, DefaultWeightedEdge> shortestPath5 = shortestPath.getPath(v2, v3);

        // [(v1 : v2), (v2 : v3)]
        System.out.println(shortestPath1.toString());

        // [(v1 : v2)]
        System.out.println(shortestPath2.toString());

        // [v1]
        System.out.println(shortestPath3.toString());

        //Path is not connected, all returns null
        Assert.assertNull(shortestPath4);

        // [(v2 : v3)]
        System.out.println(shortestPath5.toString());
    }

Example 5: Directed weighted graph

Get the shortest path from v0 to v7

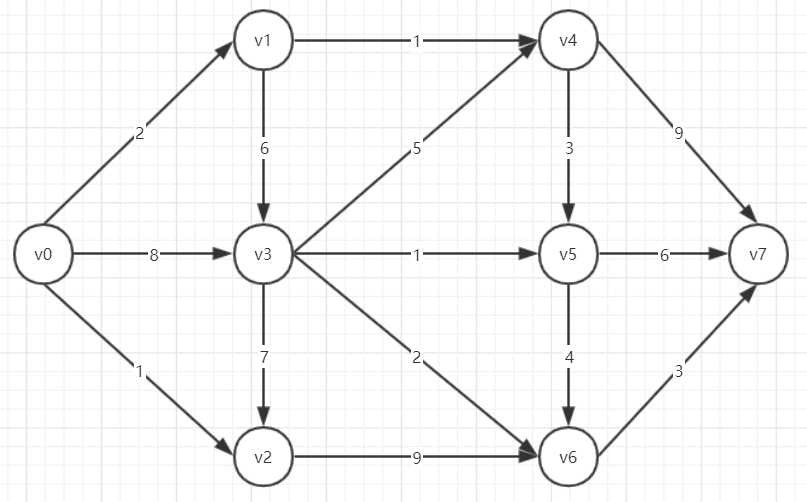
    @Test
    public void testDirectedWeightedGraph() {
        SimpleDirectedWeightedGraph<String, DefaultWeightedEdge> graph = createGraph();
        printShortestPath(graph);
    }

    /**
     * Create a directed weighted graph
     */
    public SimpleDirectedWeightedGraph<String, DefaultWeightedEdge> createGraph() {

        String[] str = {"v0", "v1", "v2", "v3", "v4", "v5", "v6", "v7"};
        int[] startPoint = {0, 0, 0, 1, 1, 3, 3, 3, 3, 2, 4, 5, 5, 4, 6};
        int[] endPoint =   {1, 3, 2, 4, 3, 4, 5, 6, 2, 6, 5, 6, 7, 7, 7};
        double[] weights = {2, 8, 1, 1, 6, 5, 1, 2, 7, 9, 3, 4, 6, 9, 3};

        SimpleDirectedWeightedGraph<String, DefaultWeightedEdge> directedGraph =
                new SimpleDirectedWeightedGraph<>(DefaultWeightedEdge.class);

        //add vertex
        for (String s : str) {
            directedGraph.addVertex(s);
        }

        // Starting point
        DefaultWeightedEdge[] edgeSources = new DefaultWeightedEdge[startPoint.length];
        // End
        DefaultWeightedEdge[] edgeTargets = new DefaultWeightedEdge[startPoint.length];

        for (int i = 0; i < endPoint.length; i++) {
            edgeSources[i] = directedGraph.addEdge(str[startPoint[i]], str[endPoint[i]]);
            edgeTargets[i] = directedGraph.addEdge(str[endPoint[i]], str[startPoint[i]]);
            directedGraph.setEdgeWeight(edgeSources[i], weights[i]);
            directedGraph.setEdgeWeight(edgeTargets[i], weights[i]);
        }
        return directedGraph;
    }

    /**
     * Based on the resulting weighted directed graph, Dijkstra calculates the shortest path and saves the sum of their path weights into the array Dij
     */
    public static void printShortestPath(SimpleDirectedWeightedGraph<String, DefaultWeightedEdge> graph) {

        DijkstraShortestPath<String, DefaultWeightedEdge> dijkstraAlg = new DijkstraShortestPath<>(graph);

        //Get the shortest path from u0 to u7
        System.out.println("Shortest path from v1 to v8:");
        ShortestPathAlgorithm.SingleSourcePaths<String, DefaultWeightedEdge> sourcePaths = dijkstraAlg.getPaths("v0");
        GraphPath<String, DefaultWeightedEdge> u0ToU7ShortestPath = sourcePaths.getPath("v7");

        //Print Path
        List<String> pathsList = u0ToU7ShortestPath.getVertexList();
        StringBuilder sb = new StringBuilder();
        boolean firstElement = true;
        for (String s : pathsList) {
            if (firstElement) {
                sb.append(s);
                firstElement = false;
            } else {
                sb.append("->").append(s);
            }
        }
        System.out.println(sb);

        System.out.println("Shortest path weight:" + u0ToU7ShortestPath.getWeight());
    }

Output:

Shortest path from v0 to v7:
v0->v1->v4->v7
Shortest path weight:12.0