Title:

Train of thought:

Map building.
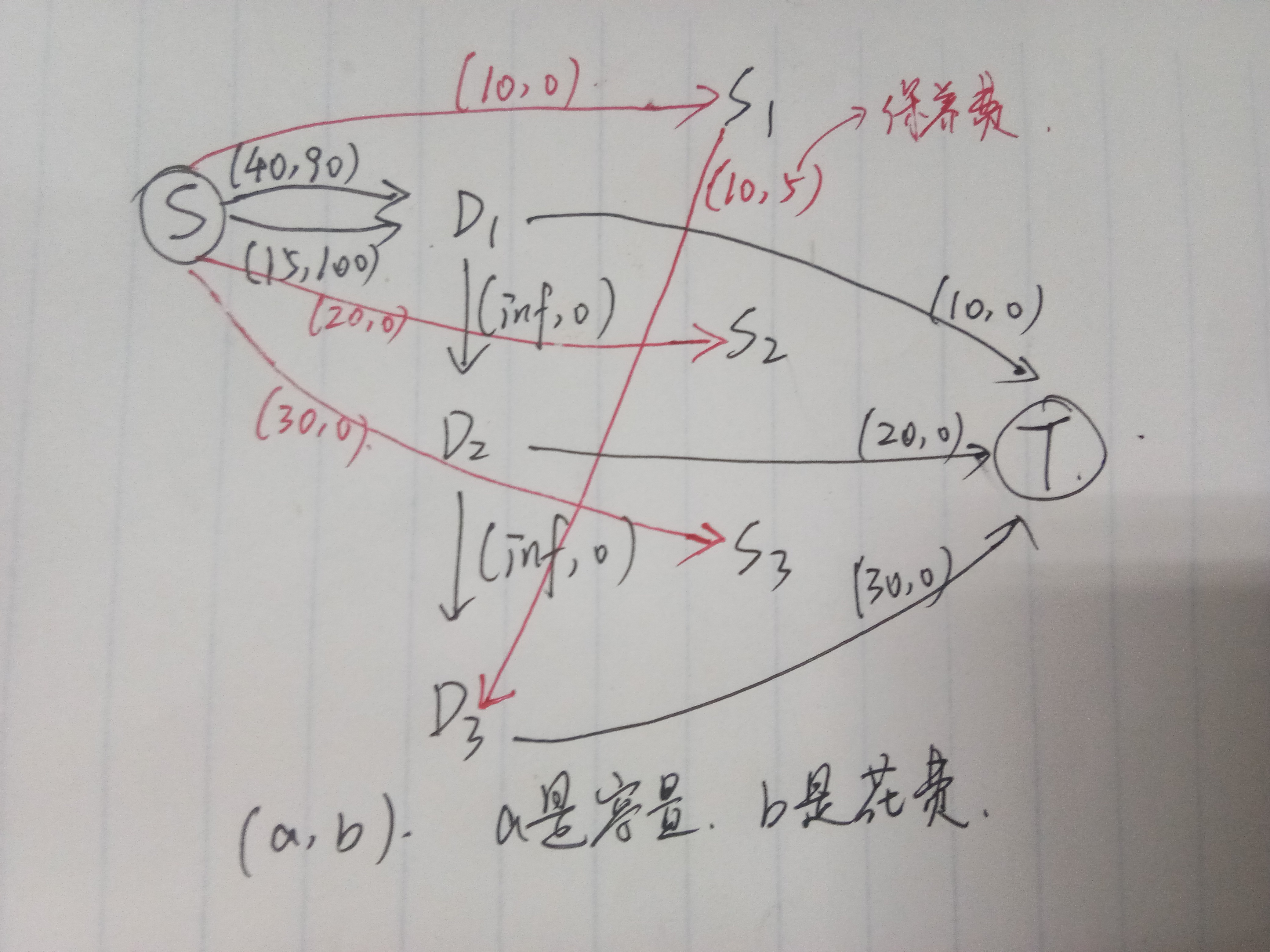
Set up two nodes Di and Si for each day, which respectively represent the car in the rental company and the car returned on the same day. From the source point S to the first day D1, the information of the car company is connected. The capacity INF of di - > DJ, with a cost of 0, indicates that the car in the car rental company can be rented out and stored in the company.
Si - > DJ means that the returned car can be rented out again on day (i + di + 1). Each di - > T company has a current planned lease out number.
After running, check whether the edge of di - > t is full. If it doesn't mean that the planned task can't be completed one day, there is no solution.
Here is an example, corresponding to the first input data.
3 2 1
10 20 30
40 90 15 100
1 5

#include <cstdio>
#include <queue>
#include <vector>
#include <cstring>
#include <algorithm>
#define fi first 
#define se second
#define pii pair<int,int>
using namespace std;
const int INF = 0x3f3f3f3f;
typedef long long LL;
const int maxn = 200+10;
int N, C, R;

// chart
struct Edge{
	int u,v,cap,flow,cost;
	Edge(int u, int v, int cap, int f, int cost):u(u),v(v),cap(cap),flow(f),cost(cost){}
};
vector<Edge> edges;
vector<int> G[maxn];
void init(int a){
	for(int i = 0; i < a; ++i) G[i].clear();
	edges.clear();
}
void addEdge(int u, int v, int cap, int cost){
	edges.push_back(Edge(u,v,cap,0,cost));
	edges.push_back(Edge(v,u,0,0,-cost));
	int m = edges.size();
	G[u].push_back(m-2);
	G[v].push_back(m-1);
}

int pre[maxn], dis[maxn], asc[maxn], inq[maxn];
bool Bellman(int s, int t, int& flow, LL& cost){
	for(int i = 0; i < N*2+2; ++i){ dis[i] = INF; inq[i] = 0; }
	queue<int> Q;
	Q.push(s);
	dis[s] = 0; inq[s] = 1; asc[s] = INF;
	while(!Q.empty()){
		int x = Q.front(); Q.pop();
		inq[x] = 0;
		for(int i = 0; i < G[x].size(); ++i){
			Edge& e = edges[G[x][i]];
			if(dis[e.v] > dis[x] + e.cost&&e.cap > e.flow){
				dis[e.v] = dis[x] + e.cost;
				pre[e.v] = G[x][i];
				asc[e.v] = min(asc[x], e.cap - e.flow);
				if(!inq[e.v]){ Q.push(e.v); inq[e.v] = 1;}
			}
		}
	}
	if(dis[t] == INF) return false;
	flow += asc[t];
	cost+= (LL)asc[t] * (LL)dis[t];
	for(int u = t; u != s; u = edges[pre[u]].u){
		edges[pre[u]].flow += asc[t];
		edges[pre[u]^1].flow -= asc[t];
	}
	return true;
}

int MCMF(int s, int t, LL& cost){
	int flow = 0; cost = 0;
	while(Bellman(s, t, flow, cost));
	return flow;
}

int main()
{
	freopen("in.txt","r",stdin);
	int T; scanf("%d",&T);
	int kase = 1;
	while(T--){
		
		scanf("%d%d%d",&N,&C,&R);init(2*N+2);
		int s = 0, t = 2*N+1;
		
		int sum = 0;
		for(int i = 1; i <= N; ++i) {
			int x; scanf("%d",&x); addEdge(s, i, x, 0);	// s -> Q
			if(i < N) addEdge(N+i, N+i+1, INF, 0);	// gi -> gj
			addEdge(N+i, t, x, 0);		// g -> t
			sum+= x;
		}
		for(int i = 1; i <= C; ++i) {
			int a,b; scanf("%d%d", &a, &b); addEdge(s, N+1, a, b);	// s -> g
		}
		for(int i = 0; i < R; ++i){
			int d, s; scanf("%d%d", &d, &s);
			for(int j = 1; j <= N; ++j){
				if(j + d + 1 <= N) addEdge(j, N+j+d+1, INF, s);		// q -> g
			}
		}
		
		LL ans;
		int maxflow = MCMF(s, t, ans);
		
		printf("Case %d: ", kase++);
		if(sum != maxflow) printf("impossible\n");	// inspect
		else printf("%lld\n",ans);
	}

	return 0;
}