1. Problem Description

How to understand the following array in openGL:

const float vertices[] = {                  //Cube array
	-0.5f, -0.5f, -0.5f, 1.0f,0.0f,0.0f,
	0.5f, -0.5f, -0.5f,  1.0f,0.0f,0.0f,
	0.5f,  0.5f, -0.5f,  1.0f,0.0f,0.0f,
	0.5f,  0.5f, -0.5f,  1.0f,0.0f,0.0f,
	-0.5f,  0.5f, -0.5f,  1.0f,0.0f,0.0f,
	-0.5f, -0.5f, -0.5f,  1.0f,0.0f,0.0f,

	-0.5f, -0.5f,  0.5f,  0.0f,1.0f,0.0f,
	0.5f, -0.5f,  0.5f,  0.0f,1.0f,0.0f,
	0.5f,  0.5f,  0.5f,  0.0f,1.0f,0.0f,
	0.5f,  0.5f,  0.5f,  0.0f,1.0f,0.0f,
	-0.5f,  0.5f,  0.5f,  0.0f,1.0f,0.0f,
	-0.5f, -0.5f,  0.5f,  0.0f,1.0f,0.0f,

	-0.5f,  0.5f,  0.5f,  0.0f,0.0f,1.0f,
	-0.5f,  0.5f, -0.5f,  0.0f,0.0f,1.0f,
	-0.5f, -0.5f, -0.5f,  0.0f,0.0f,1.0f,
	-0.5f, -0.5f, -0.5f,  0.0f,0.0f,1.0f,
	-0.5f, -0.5f,  0.5f,  0.0f,0.0f,1.0f,
	-0.5f,  0.5f,  0.5f,  0.0f,0.0f,1.0f,

	0.5f,  0.5f,  0.5f,  0.5f,0.0f,0.0f,
	0.5f,  0.5f, -0.5f,  0.5f,0.0f,0.0f,
	0.5f, -0.5f, -0.5f,  0.5f,0.0f,0.0f,
	0.5f, -0.5f, -0.5f,  0.5f,0.0f,0.0f,
	0.5f, -0.5f,  0.5f,  0.5f,0.0f,0.0f,
	0.5f,  0.5f,  0.5f,  0.5f,0.0f,0.0f,

	-0.5f, -0.5f, -0.5f,  0.0f,0.5f,0.0f,
	0.5f, -0.5f, -0.5f,  0.0f,0.5f,0.0f,
	0.5f, -0.5f,  0.5f,  0.0f,0.5f,0.0f,
	0.5f, -0.5f,  0.5f,  0.0f,0.5f,0.0f,
	-0.5f, -0.5f,  0.5f,  0.0f,0.5f,0.0f,
	-0.5f, -0.5f, -0.5f,  0.0f,0.5f,0.0f,

	-0.5f,  0.5f, -0.5f,  0.0f,0.0f,0.5f,
	0.5f,  0.5f, -0.5f,  0.0f,0.0f,0.5f,
	0.5f,  0.5f,  0.5f,  0.0f,0.0f,0.5f,
	0.5f,  0.5f,  0.5f,  0.0f,0.0f,0.5f,
	-0.5f,  0.5f,  0.5f,  0.0f,0.0f,0.5f,
	-0.5f,  0.5f, -0.5f,  0.0f,0.0f,0.5f
};

2. Question Solutions

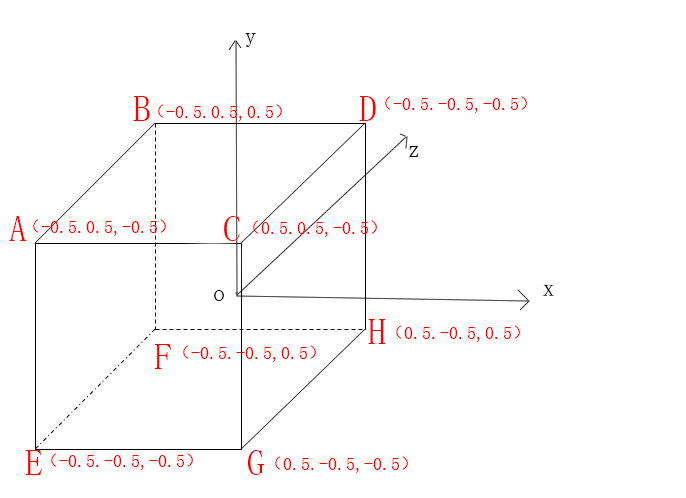
Every three rows is a triangle.
The first three values of each line are the position of each point in the space of the triangle, and the last three values are the color or normal vector.
The cube has six faces, each of which needs two triangles to be joined together to form one face of the cube. There are 12 triangles in the cube.
So there are 12 3-line points after the code is separated.

const float vertices[] = {                  //Cube array
/*------------------Triangular EGC*/
 -0.5f, -0.5f, -0.5f, 1.0f,0.0f,0.0f,//E
 0.5f, -0.5f, -0.5f,  1.0f,0.0f,0.0f,//G
 0.5f,  0.5f, -0.5f,  1.0f,0.0f,0.0f,//C
  
 /*------------------Triangular CAE*/
 0.5f,  0.5f, -0.5f,  1.0f,0.0f,0.0f,//C
 -0.5f,  0.5f, -0.5f,  1.0f,0.0f,0.0f,//A
 -0.5f, -0.5f, -0.5f,  1.0f,0.0f,0.0f,//E
  
  /*------------------Triangular FHD*/
 -0.5f, -0.5f,  0.5f,  0.0f,1.0f,0.0f,//F
 0.5f, -0.5f,  0.5f,  0.0f,1.0f,0.0f,//H
 0.5f,  0.5f,  0.5f,  0.0f,1.0f,0.0f,//D
  
  /*------------------Triangular DBF*/
 0.5f,  0.5f,  0.5f,  0.0f,1.0f,0.0f,//D
 -0.5f,  0.5f,  0.5f,  0.0f,1.0f,0.0f,//B
 -0.5f, -0.5f,  0.5f,  0.0f,1.0f,0.0f,//F
  
  /*------------------Triangle BAE----------------------*/
 -0.5f,  0.5f,  0.5f,  0.0f,0.0f,1.0f,//B
 -0.5f,  0.5f, -0.5f,  0.0f,0.0f,1.0f,//A
 -0.5f, -0.5f, -0.5f,  0.0f,0.0f,1.0f,//E
  
  /*------------------Triangular EFB*/
 -0.5f, -0.5f, -0.5f,  0.0f,0.0f,1.0f,//E
 -0.5f, -0.5f,  0.5f,  0.0f,0.0f,1.0f,//F
 -0.5f,  0.5f,  0.5f,  0.0f,0.0f,1.0f,//B
  
  /*------------------Triangular DCG*/
 0.5f,  0.5f,  0.5f,  0.5f,0.0f,0.0f,//D
 0.5f,  0.5f, -0.5f,  0.5f,0.0f,0.0f,//C
 0.5f, -0.5f, -0.5f,  0.5f,0.0f,0.0f,//G
  
  /*------------------Triangular GHD*/
 0.5f, -0.5f, -0.5f,  0.5f,0.0f,0.0f,//G
 0.5f, -0.5f,  0.5f,  0.5f,0.0f,0.0f,//H
 0.5f,  0.5f,  0.5f,  0.5f,0.0f,0.0f,//D
  
  /*------------------Triangular EGH*/
 -0.5f, -0.5f, -0.5f,  0.0f,0.5f,0.0f,//E
 0.5f, -0.5f, -0.5f,  0.0f,0.5f,0.0f,//G
 0.5f, -0.5f,  0.5f,  0.0f,0.5f,0.0f,//H
  
  /*------------------Triangle HFE*/
 0.5f, -0.5f,  0.5f,  0.0f,0.5f,0.0f,//H
 -0.5f, -0.5f,  0.5f,  0.0f,0.5f,0.0f,//F
 -0.5f, -0.5f, -0.5f,  0.0f,0.5f,0.0f,//E
  
  /*------------------Triangle ACD*/
 -0.5f,  0.5f, -0.5f,  0.0f,0.0f,0.5f,//A
 0.5f,  0.5f, -0.5f,  0.0f,0.0f,0.5f,//C
 0.5f,  0.5f,  0.5f,  0.0f,0.0f,0.5f,//D
  
  /*------------------Triangular DBA*/
 0.5f,  0.5f,  0.5f,  0.0f,0.0f,0.5f,//D
 -0.5f,  0.5f,  0.5f,  0.0f,0.0f,0.5f,//B
 -0.5f,  0.5f, -0.5f,  0.0f,0.0f,0.5f//A
};

3.EBO Representation

If you use EBO, the difference between vertices array and the previous one is that the repetitive points do not need to be written out again, write a line, and then record the position (which line) of the vertices array.
Open a new indices array. Each number in the indices array corresponds to the point in the previous vertice array (the location of the previous record), and each row represents a triangle. The code is as follows:

float vertices[] = {
 
        -0.5f,0.5f,-0.5f,   0.0f, 0.0f, 0.0f,//Point A 0
        -0.5f,0.5f,0.5f,    0.0f, 0.0f, 1.0f,//Point B 1
        0.5f,0.5f,-0.5f,    0.0f, 1.0f, 0.0f,//Point C 2
        0.5f,0.5f,0.5f,     0.0f, 1.0f, 1.0f,//Point D 3
         
        -0.5f,-0.5f,-0.5f,  1.0f, 0.0f, 0.0f,//Point E 4
        -0.5f,-0.5f,0.5f,   1.0f, 0.0f, 1.0f,//Point F 5
        0.5f,-0.5f,-0.5f,   1.0f, 1.0f, 0.0f,//Point G 6
        0.5f,-0.5f,0.5f,    1.0f, 1.0f, 1.0f//Point H 7
 
     };
 
    unsigned int indices[] = {
        /*Above ABC,BCD*/
        0,1,2,
        1,2,3,
 
        /*Following EFG,FGH*/
        4,5,6,
        5,6,7,
        /*Left ABF,AEF*/
        0,1,5,
        0,4,5,
        /*Right side CDH,CGH*/
        2,3,7,
        2,6,7,
        /*ACG,AEG*/
        0,2,6,
        0,4,6,
        /*Behind BFH,BDH*/
        1,5,7,
        1,3,7
    };

Reference article:

https://www.jianshu.com/p/12b0c198c2e0
https://blog.csdn.net/dcrmg/article/details/53556664