Bibliography: 2022 data structure review guide for postgraduate entrance examination organized by Kingway Forum

1. Delete the element with the minimum value from the sequence table (assuming unique) and return the value of the deleted element by the function. The empty position is filled by the last element. If the sequence table is empty, an error message is displayed and the operation is exited.

• Algorithm idea: search the whole sequence table, find the minimum value element and remember its position. After the search, fill the empty position of the original minimum value element with the last element.

#include<iostream>
using namespace std;
#define InitSize 9
#define MaxSize 14
typedef struct
{
	int data[InitSize];
	int length; //Current length of linear table
}SqList;

bool DelEle(SqList &L, int &min) //The formal parameter is a reference type
{
	int i, j;
	min = L.data[0]; //Assume that the first element is the minimum
	if (L.length == 0) //If the linear table is empty
	{
		cout<<"The Sequence List is Empty!"<<endl; //Output error message
		return false; //Exit operation
	}
	 //If the linear table is not empty
	for (i = 1; i < L.length-1; i++) //From the second element to the last element in the linear table
		if (L.data[i] < min) //If a value smaller than the first element appears after it
		{
			min = L.data[i]; //Sets the current value to the minimum
			j = i; //Records the subscript of the current value element
		}
	L.data[j] = L.data[L.length - 1]; //The empty position is filled by the last element
	L.length--; //Current length of linear table - 1
	return true; //Exit operation
}

int main()
{
	SqList L;
	int i,min;
	L.length = InitSize;
	int a[10] = { 3,6,1,2,4,0,9,7,8,5 };
	for (i = 0; i < L.length; i++)
		L.data[i] = a[i]; //Assign values to linear tables
	cout<<"The values in the deletion table are:"<<endl;	
	for (i = 0; i < L.length; i++)
		cout << L.data[i] << ' '; //The output deletes the values in the frontline table
	cout << "\n";
	cout << boolalpha << DelEle(L, min) << endl; //Call the function and return success or failure
	cout << "After deletion, the values in the linear table are:" << endl;
	for (i = 0; i < L.length; i++)
		cout << L.data[i] << ' '; //Outputs the values in the linear table after deletion
	cout << "\n";
	cout << "The deleted element values are:" << min << endl; //Output the value of the deleted element
	return 0;
}

Program analysis:

• The function needs to use Boolean type for judgment, so it is written in C + +.
• Operation results:
  
• Time complexity: O(n); Space complexity: O(1)

2. Invert all elements of sequence table L.

• Algorithm idea: scan the first half of the elements of the sequence table L L . d a t a [ i ] ( 0 ≤ i < L . l e n g t h 2 ) L.data[i](0≤i<\frac{L.length}{2}) 50. Data [i] (0 ≤ I < 2L. Length) and compare it with the corresponding element in the second half L . d a t a [ L . l e n g t h − i − 1 ] L.data[L.length-i-1] 50. Data [L.Length − i − 1].

#include<stdio.h>
#define InitSize 9
#define MaxSize 14
typedef struct
{
	int data[InitSize];
	int length; //Current length of linear table
}SqList;

void DiverseElem(SqList &L)
{
	int i, t;
	for(i=0;i<L.length/2;i++) //The loop ends in the middle of the linear table
	{ 
		t = L.data[i]; L.data[i] = L.data[L.length - 1 - i]; L.data[L.length - 1 - i] = t;
	} //The first element is exchanged with the last element; The second element exchanges with the penultimate element
}

int main()
{
	int i;
	SqList L;
	L.length = InitSize; //The current length of the linear table is 9
	int a[10] = { 3,5,4,1,7,3,8,0,1,6 }; //Assign 10 numbers to array a
	printf("The values of each element in the interchangeability table are:\n");
	for (i = 0; i < L.length; i++)
		L.data[i] = a[i]; //Assign a value to the linear table and assign only 9 values
	for (i = 0; i < L.length; i++)
		printf("%d ",L.data[i]);
	printf("\n");
	DiverseElem(L); //Call function, inverse element
	printf("The values of each element in the interchangeability table are:\n");
	for (i = 0; i < L.length; i++)
		printf("%d ", L.data[i]);
	return 0;
}

Program analysis:

• Operation results:
  
• Time complexity: O ( n 2 ) O(\frac{n}{2}) O(2n​)； Space complexity: O(1)

3. For the sequence table L with length n, delete all data elements with value x in the linear table.

Refer to the corresponding fourth question in the link, which has two solutions.
Click!

4. Delete all elements whose values are between the given values s and t (s < T is required) from the ordered sequence table. If s or T is unreasonable or the sequence table is empty, an error message will be displayed and the operation will be exited.

Algorithm idea: first find the first element with value ≥ s (the first deleted element), and then find the first element with value > t (the next element of the last deleted element). To delete this element, just move the following element forward directly.

bool DelEle(SqList &L, int s, int t)
{
	int i, j;
	if (s >= t || L.length == 0) If entered s>t Or the linear table is empty
	{
		printf("data error!"); //Display error message
		return false;
	}
	for (i = 0; i < L.length && L.data[i] < s; i++); //Loop to find the first element greater than or equal to s
	if (i >= L.length) //If the value of each element in the linear table is less than s
	{
		printf("No element delete.\n"); //Then there are no elements to delete
		return false;
	}
	for (j = i; j < L.length && L.data[j] < t; j++); //Loop to find the first element greater than t
	for(;j<L.length;j++,i++)
		L.data[i] = L.data[j];
	L.length = i+1;
	return true;
}
DelEle(L,4,6);

Program analysis:

• ! Note: this question is different from the previous one. Because it is an ordered table, the deleted elements must be connected as a whole.
• Operation results:
  
• Time complexity: O(n); Space complexity: O(1)

5. Delete all elements whose values are between the given values s and t (including s and T, requiring s < T) from the sequence table. If s or T is unreasonable or the sequence table is empty, an error message will be displayed and the operation will be exited.

Algorithm idea: scan the sequence table L from front to back, and use count to record the number of elements with element values between s and t (initially count=0). For the currently scanned element, if its value is not between s and T, move forward count positions; Otherwise, execute count + +. In this way, each element not between s and t is moved only once, so the algorithm is efficient.

Refer to the solution 2 of the fourth problem in the link.
Click!

bool DelEle(SqList& L, int s, int t)
{
	int i, count = 0; //Count is used to count the number of deleted elements
	if (s >= t || L.length == 0) //If the entered s > t or the linear table is empty
		return false; //Exit operation
	for (i = 0; i < L.length && L.data[i] < s; i++);
	if (i > L.length) //There are no elements to delete
		return false;
	for (i = 0; i < L.length; i++)
		{
			if (L.data[i] >= s && L.data[i] <= t) //If the element is in the range of [s,t]
				count++; //Count value + 1
			else
				L.data[i - count] = L.data[i]; //Otherwise, move other elements forward
		}
		L.length -= count; //The current length of the linear table after the element is deleted
		return true;
}
DelEle(L,3,7);

Program analysis:

• The function needs to use Boolean type for judgment, so it is written in C + +.
• Operation results:
  
• Time complexity: O(n); Space complexity: O(1)

6. Delete all elements with duplicate values from the ordered order table to make the values of all elements in the table different.

• Algorithm idea: initially, the first element is regarded as a non repeated ordered table. Then judge whether the following elements are the same as the last element of the previous non repeated ordered table in turn. If they are the same, continue to judge backward; If it is different, insert the last of the previous non repeating ordered table until the end of the table is judged.

bool DelEle(SqList &L)
{
	int i, count=0;
	if (L.length == 0) //If the linear table is empty, an error is returned
		return false;
	for (i = 1; i < L.length && L.data[i] != L.data[i - 1]; i++);
	if (i >= L.length) //If there are no duplicate elements in the linear table, an error is returned
		return false;
	for (i = 1; i < L.length; i++)
	{
		if (L.data[i] == L.data[i - 1]) //If the latter element has the same value as the previous element
			count++; //Count value + 1
		else L.data[i - count] = L.data[i]; //If not, move the following elements forward by count bit
	}
	L.length -= count; //Modify the current length of the linear table
	return true;
}
DelEle(L);

Program analysis:

• ! Note: it is an ordered order table. Elements with the same value must be in continuous positions, using the idea similar to direct insertion sorting.
• Operation results:
  
• Time complexity: O(n); Space complexity: O(1)

7. Merge the two ordered order tables into a new ordered order table, and the function returns the result order table.

• Algorithm idea: firstly, the smaller nodes in the header of the two sequence tables are continuously removed in order and stored in the new sequence table. Then, which table has the rest, add the rest to the new sequence table.

bool ConEle(SqList L1,SqList L2,SqList &L)
{
	if (L1.length + L2.length > L.maxsize) //If the sum of the lengths of two linear tables is greater than the maximum length of the third linear table
		return false; //An error is returned
	int i=0, j=0, k=0;
	while (i < L1.length && j < L2.length) //The cycle range of i is the shortest length of the two linear tables
	{
		if (L1.data[i] <= L2.data[j]) //Compare two by two and store the smaller value in the new table
			L.data[k++] = L1.data[i++];
		else L.data[k++] = L2.data[j++];
	}
	while (i < L1.length) //Indicates that the length of the first table is greater than that of the second table
		L.data[k++] = L1.data[i++]; //Copy all redundant elements of the first table to the end of the new table
	while (j < L2.length) //Indicates that the second table is longer than the first table
		L.data[k++] = L2.data[j++]; //Copy all redundant elements of the second table to the end of the new table
	L.length = k+1;
	return true;
}
ConEle(L1,L2,L);

Program analysis:

• Operation results:
  
• Time complexity: O(n); Space complexity: O(1)

8. Known in one-dimensional array A [ m + n ] A[m+n] Two linear tables are stored in sequence in A[m+n] ( a 1 , a 2 , a 3 , ... , a m ) (a_1,a_2,a_3,...,a_m) (a1, a2, a3,..., am) and ( b 1 , b 2 , b 3 , . . . , b n ) (b_1,b_2,b_3,...,b_n) (b1​,b2​,b3​,...,bn​). Try to write a function to exchange the positions of the two sequential tables in the array ( b 1 , b 2 , b 3 , . . . , b n ) (b_1,b_2,b_3,...,b_n) (b1, b2, b3,..., bn) on ( a 1 , a 2 , a 3 , ... , a m ) (a_1,a_2,a_3,...,a_m) In front of (a1, a2, a3,..., am).

• Algorithm idea: first all the elements in array A[m+n] ( a 1 , a 2 , a 3 , . . . , a m , b 1 , b 2 , b 3 , ... , b n ) (a_1,a_2,a_3,...,a_m,b_1,b_2,b_3,...,b_n) (a1, a2, a3,..., am, b1, b2, b3,..., bn) reversed in place as ( b n , b n − 1 , b n − 2 , . . . , b 1 , a m , a m − 1 , a m − 2 , . . . , a 1 ) (b_n,b_{n-1}, b_{n-2},...,b_1,a_m,a_{m-1},a_{m-2},...,a_1) (bn, bn − 1, bn − 2,..., b1, am, am − 1, am − 2,..., a1), and then use the inverse algorithm for the first n elements and the last m elements respectively ( b 1 , b 2 , b 3 , ... , b n , a 1 , a 2 , a 3 , . . . , a m ) (b_1,b_2,b_3,...,b_n,a_1,a_2,a_3,...,a_m) (b1, b2, b3,..., bn, a1, a2, a3,..., am), so as to realize the position exchange of the sequence table

void RevEle2(SqList &L,int x,int y) //Inverse function
{
	int i = x, j =(y-x)/2, m=y, t;
	//x is the starting subscript value of array exchange, and y is the last subscript value of array exchange
	//j is the number of cycles required for array exchange
	while(j)
	{
		t = L.data[i]; L.data[i] = L.data[m - 1]; L.data[m - 1] = t;
		i++; m--;//The subscript value of the element in front of the array increases and the subscript value of the element behind the array decreases
		j--; //Number of cycles - 1
	}
}

void RevEle1(SqList &L1, SqList &L2, SqList &L)
{
	
	RevEle2(L, 0, L.length); //First exchange: array subscript range 0 ~ 14
	RevEle2(L, 0, L2.length); //Second exchange: array subscript range 0 ~ 5
	RevEle2(L, L2.length, L.length); //The third exchange: array subscript range 6 ~ 14
}
RevEle1(L1, L2, L);

Program analysis:

• Operation results:
  
• The time complexity of the three RevEle functions are: O ( m + n 2 ) , O ( n 2 ) , O ( m 2 ) O(\frac{m+n}{2}),O(\frac{n}{2}),O(\frac{m}{2}) O(2m+n​),O(2n​),O(2m​)
• Time complexity: O(m+n); Space complexity: O(1)

9. Linearity table ( a 1 , a 2 , a 3 , ... , a n ) (a_1,a_2,a_3,...,a_n) The elements in (a1, a2, a3,..., an) are incrementally ordered and stored in the computer in order. It is required to design an algorithm to find the element with the value of x in the table in the least time. If it is found, it will be exchanged with the position of the subsequent element. If it is not found, it will be inserted into the table and the elements in the table will still increase in order.

• The linear table stored in order is incremented in order, and can be searched in order or in half. The half search method is used here.

void ExchEle(SqList& L, int x)
{
	int low = 0, high = L.length - 1, mid, t, i; //low and high subscripts pointing to the lower and upper bounds of the sequence table
	while (low <= high)
	{
		mid = (low + high) / 2; //Find the middle position
		if (L.data[mid] == x) break; //Find x and exit the while loop
		else if (L.data[mid] < x) low = mid + 1; //Go to the right half of mid
		else high = mid - 1;//Go to the left half of mid
	}
	if (L.data[mid] == x && mid != L.length - 1) //If the last element is equal to x, there is no operation to exchange with its successor
	{
		t = L.data[mid]; L.data[mid] = L.data[mid + 1]; L.data[mid + 1] = t;
	}
	
	if (low > high) //Search failed, insert data element x
	{ 
		for (i = L.length - 1; i > high; i--) L.data[i + 1] = L.data[i]; //Move back element
		L.data[i + 1] = x; //Insert x
	}
}
ExchEle(L,5); 

Program analysis:

• Operation results:
  

10. Design general n ( n > 1 ) n(n>1) N (n > 1) integers are stored in one-dimensional array R. Move the sequence saved in R to the left p ( 0 < p < n ) p(0<p<n) P (0 < p < n) positions, that is, the data in R is determined by ( X 0 , X 1 , ... , X n − 1 ) (X_0,X_1,...,X_{n-1}) (X0, X1,..., Xn − 1) transform to ( X p , X p + 1 , ... , X n ー 1 , X 0 , X 1 , ... , X p − 1 ) (X_p,X_{p+1},...,X_{nー1},X_0,X_1,...,X_{p-1}) (Xp​,Xp+1​,...,Xnー1​,X0​,X1​,...,Xp−1​).

Algorithm idea: refer to question 8.

void DivEle(SqList &L, int start, int end)
{
	int i = start, j = end, mid = (j - i) / 2, t;
	//start is the starting subscript value of array exchange, and end is the last subscript value of array exchange
	//mid is the number of times the array exchange needs to be cycled
	while(mid)
	{
		t = L.data[i]; L.data[i] = L.data[j-1]; L.data[j-1] = t;
		i++; j--; //The subscript value of the element in front of the array increases and the subscript value of the element behind the array decreases
		mid--; Number of cycles-1
	}
}

void LefMov(SqList &L, int x)
{
	DivEle(L, 0, L.length); //First exchange: array subscript range 0 ~ 9
	DivEle(L, 0, L.length-x); //Second exchange: array subscript range 0 ~ 6
	DivEle(L, L.length - x, L.length); //Second exchange: array subscript range 6 ~ 9
}
LefMov(L,3);

Program analysis:

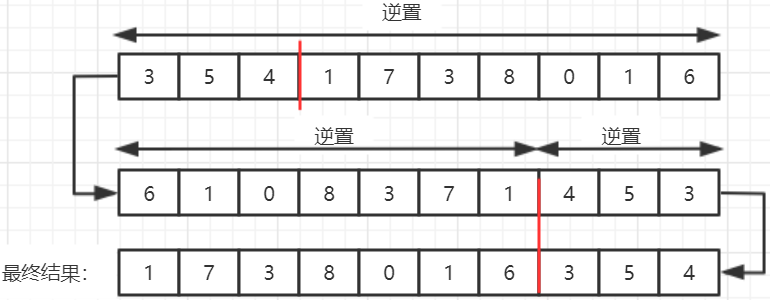
• Operation results:
  
• The time complexity of the three DivEle functions are: O ( n 2 ) , O ( n − x 2 ) , O ( x 2 ) O(\frac{n}{2}),O(\frac{n-x}{2}),O(\frac{x}{2}) O(2n​),O(2n−x​),O(2x​)
• Time complexity: O(n); Space complexity: O(1)

11. One length is L ( L ≥ 1 ) L(L≥1) The ascending sequence S of L(L ≥ 1) is in the second position [ L 2 ] [\frac{L}{2}] The number of [2L] locations is called the median of S. The median of two sequences is the median of the ascending sequence containing all their elements. Now there are two equal length ascending sequences A and B. find the median of two sequences A and B.

• Algorithm idea: method ① - find A new storage space l, put the ascending sequence of A and B into L, and the median of L is the median of sequence A and B.
  Method ② - the idea of analogy method ①, but do not find a new space to store them, find the second [ L 2 ] [\frac{L}{2}] Elements at [2L] locations, and then return the value

Method 1: refer to question 7.

int FinMid(SqList L1,SqList L2,SqList &L)
{
	//Merge the two ordered tables A and B into A new ordered table L
	int i=0, j=0, k=0;
	while (i < L1.length && j < L2.length) 
	{
		if (L1.data[i] < L2.data[j])
			L.data[k++] = L1.data[i++];

		else L.data[k++] = L2.data[j++];
		
	}
	if (i >= L1.length) L.data[L.length - 1] = L2.data[L2.length - 1];
	if (j >= L2.length) L.data[L.length - 1] = L1.data[L1.length - 1];
	return L.data[L.length / 2-1]; //Returns the median of L
}

Method 2:

int FinMid(SqList L1,SqList L2,SqList &L)
{
	int i=0, j=0, k=0;
	while (i < L1.length && j < L2.length)
	{
		if (L1.data[i] <= L2.data[j])
			i++;
		else j++;
		if (i + j == (L.length - 1) / 2) break; //Locate L/2
	}
	if (i == j) //If i=j at the end of the loop, the element values at the i,j positions are compared
	{
		if (L1.data[i] < L2.data[j]) return L1.data[i]; //The smaller value is the median
		return L2.data[j];
	}
	else //If i ≠ j after the end of the cycle
	{
		if (i < j) return L1.data[i]; //If J > I, the number with subscript i in A is returned
		return L2.data[j]; //If I > J, the number with subscript j in B is returned
	}
}

Program analysis:

Method 1:

• Operation results:
  
• Time complexity: O(n); Space complexity: O(n)

Method 2:

• Operation results:
  
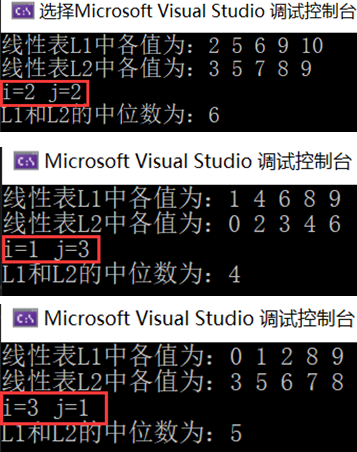
• Time complexity: O(n); Space complexity: O(1)

12. An integer sequence A = ( a 0 , a 1 , , ... , a n − 1 ) A=(a_0,a_1,,...,a_{n-1}) A=(a0, a1,,..., an − 1), where 0 ≤ a i ≤ m ( 0 ≤ i < n ) 0≤a_i≤m(0≤i<n) 0 ≤ ai ≤ m(0 ≤ I < n), if any a p 1 = a p 2 = . . . = a p m = x a_{p1}=a_{p2}=...=a_{pm}=x ap1​=ap2​=...= apm = x and m > n 2 ( 0 ≤ p k < n ， 1 ≤ k ≤ m ) m>\frac{n}{2}(0≤p_k<n，1≤k≤m) m> 2n (0 ≤ pk < n, 1 ≤ k ≤ m), then x is called the main element of A. Suppose n elements in a are saved in a one-dimensional array, find the main element of A. If there is a main element, the element is output; Otherwise, output - 1.

• Algorithm idea: create an array b with the same length as L, and assign all element values in array b to the initial value of 0. Loop traversal. Count the number of occurrences of elements with array b. the subscript of the array corresponds to the value of i. Loop again to find the maximum value in array b and record the array subscript of the value. Determine whether the maximum value is > n 2 >\frac{n}{2} >2n, if yes, the array subscript value of the tag is returned, otherwise - 1 is returned.

int FinEle(SqList L)
{
	int i = 0, max, mark;
	int b[InitSize] = { 0 }; Define array b，And assignment
	for (i = 0; i < L.length; i++) //Loop traversal
		b[L.data[i]]++ ; //Count the number of occurrences of each element in L
	max = b[0]; //Assume that the first element is the maximum
	for (i = 1; i < L.length; i++) //Loop traversal
		if (b[i] > max) //If the number is greater than the maximum value of the current tag
		{
			max = b[i]; //max reassign
			mark = i; //Record the subscript of the maximum value
		}
	if (b[mark] > L.length / 2) return mark; //Judge whether the number appears more than half the length
	else return -1;
}
FinEle(L);

Program analysis:

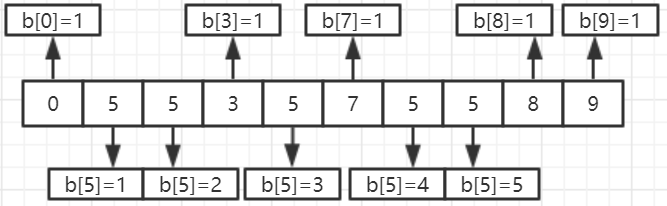
• Operation results:
  
• Time complexity: O(n); Space complexity: O(n)

13. Given a n ( n ≥ 1 ) n(n≥1) An array of n(n ≥ 1) integers to find the smallest positive integer that does not appear in the array.

• Algorithm idea: refer to question 12. After determining the b array, iterate again to find the first array subscript with 0 in the array and return the value of the subscript.

int FindEle(SqList L)
{
	int i = 0;
	int b[InitSize] = { 0 }; //Define array b and assign values
	for (i = 0; i < L.length; i++) //Loop traversal
		if(L.data[i]>=0) //Count the number of occurrences of each positive integer in L
			b[L.data[i]]++ ; //count
	for (i = 1; i < L.length; i++) //Loop traversal
		if (b[i] == 0) //Find the first subscript in the array with a value of 0
			return i; //Returns the subscript
}
FindEle(L);

Program analysis:

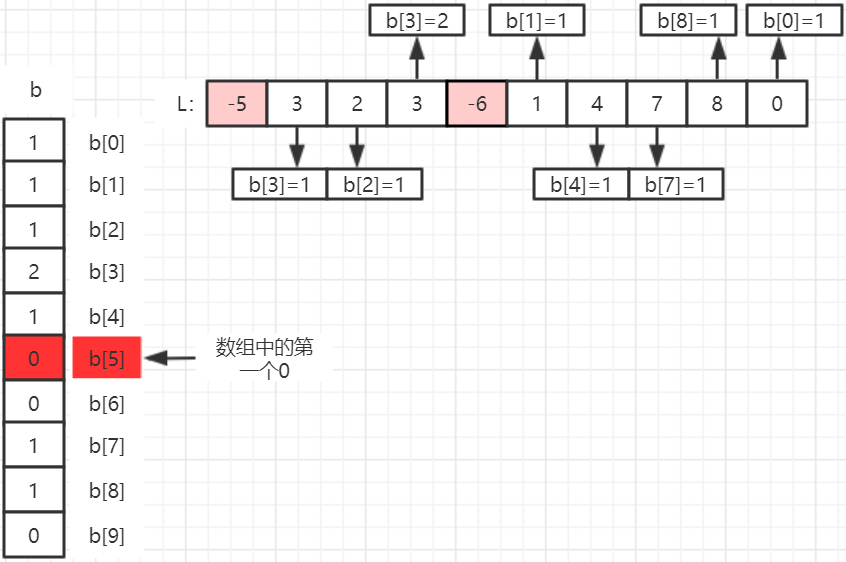
• Operation results:
  
• Time complexity: O(n); Space complexity: O(n)

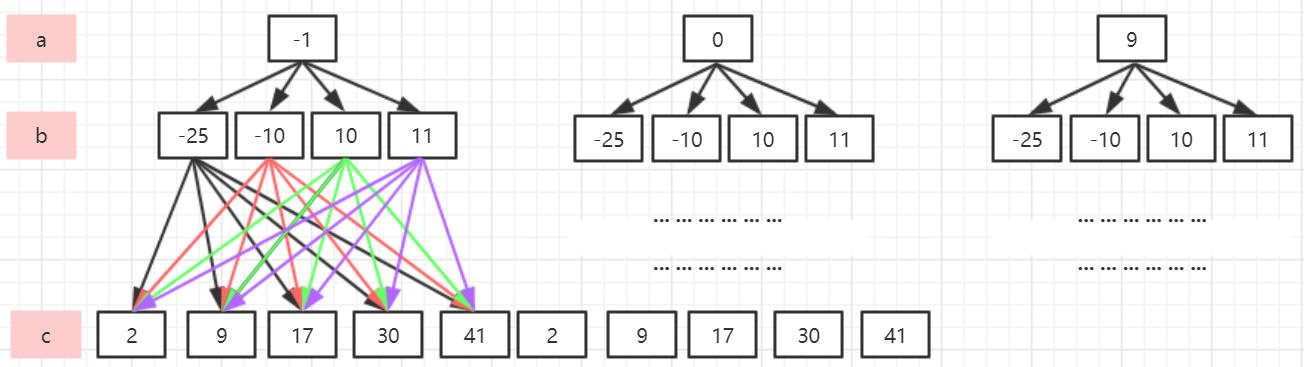
14. Define triples( a , b , c a,b,c a,b,c)( a , b , c a,b,c a. b and c are positive numbers) D = ∣ a − b ∣ + ∣ b − c ∣ + ∣ c − a ∣ D=|a-b|+|b-c|+|c-a| D=∣a−b∣+∣b−c∣+∣c−a∣. Given 3 sets of non empty integers S 1 , S 2 S_1,S_2 S1, S2 + S 3 S_3 S3, stored in three arrays in ascending order. Calculate and output all possible triples ( a , b , c ) ( a ∈ S 1 , b ∈ S 2 , c ∈ S 3 ) (a,b,c)(a∈S_1,b∈S_2,c∈S_3) (a,b,c)(a ∈ S1, b ∈ S2, C ∈ S3).

• Algorithm idea:

int MinDis(SqList a,SqList b,SqList c)
{
	int i, j, k, count = 0, min, mark , arr[60];
	for (i = 0; i < a.length; i++) //a
		for (j = 0; j < b.length; j++) //b
			for (k = 0; k < c.length; k++) //c
			{
				arr[count++] = abs(a.data[i] - b.data[j]) + abs(b.data[j] - c.data[k]) + abs(c.data[k] - a.data[i]); //Put the calculated distance into the array arr
				printf("(%d ,%d ,%d)\n", a.data[i], b.data[j], c.data[k]); //The value of the output triplet
			}
	min = arr[0]; //Assume that the first element of the array is the minimum value
	for (i = 1; i < 60; i++) //Loop through array
		if (arr[i] < min) //If a value smaller than min occurs
		{
			min = arr[i]; //Override the value of the previous min
			mark = i; //Record the array subscript of the value
		}
	return arr[mark]; //Returns the smallest value in the array
}
MinDis(S1, S2, S3);

Program analysis:

• The algorithm needs to be nested three times, and an array b needs to be created to store the distance value calculated each time. After the loop, you need to traverse array b again to find the minimum value. This method is very large in time and space, and is not a good algorithm.
  
• Operation results:
  
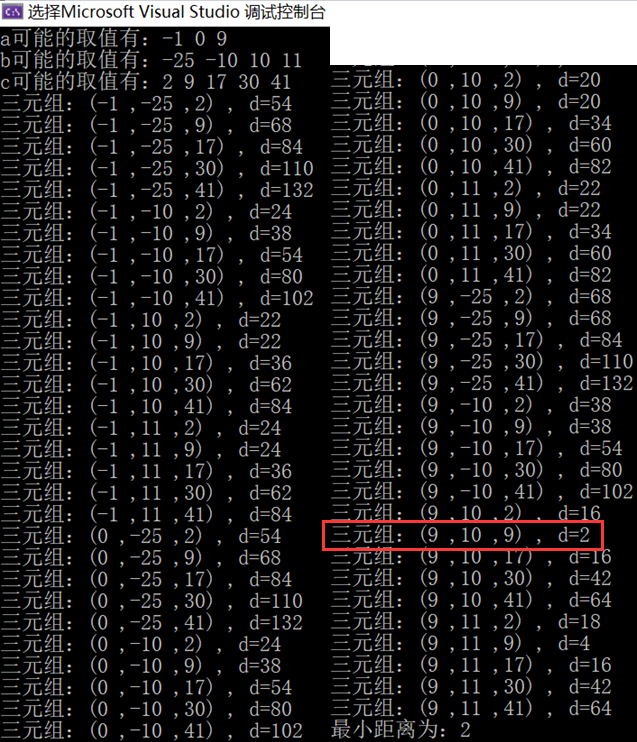
• Time complexity: O ( n 3 ) O(n^3) O(n3)； Space complexity: O ( S 1 . l e n g t h × S 2 . l e n g t h × S 3 . l e n g t h ) O(S_1.length×S_2.length×S_3.length) O(S1​.length×S2​.length×S3​.length)